Unit 4 AP Stats

Random Process

We are aware of possible outcomes but have no clue what the outcome will be (results determined by change)

There is a sense of predictability that occurs in the ____ run.

long

Patterns of random occurrences may include _____ or runs of outcome that appear to be non-random.

strings

Outcome

Result of a trial of a random process (ex: heads)

Event

A collection of outcomes (results of a trial of a random process ex: roll a prime # (2,3,5))

Simulation

A way to model random events

Law of Large Numbers

Simulated probability gets closer to theoretical probability as the number of trials increases (variability from true probability is decreased)

Conducting a simulation (with random num gen) Describe the process for FRQs

• Describe how the random digits will imitate the trial (what digits represent which outcomes). Also determine what will be recorded from each trial

• Perform many trials of the simulation

• Calculate the relative frequency of successful trials to get a calculated probability

Sample Space of Random Process

The collection of all possible non-overlapping outcomes ex: (roll a dice= [1, 2, 3, 4, 5, 6])

Probability of an event A

P(A)

Interpret Probability

Probabilities of events in repeatable situations can be interpreted as the relative frequency with which the event will occur in the long run.

Interpret Probability of P(Jazz) = 0.205

If we were to randomly select many individual albums sold this year (with replacement), the relative freq. of jazz albums selected would be approx. 0.205.

Valid probability distribution

Sum of all probabilities is 1

Complement of an event A is the event that A…

doesn’t happen

Complement of A is denoted by:

A’ or A^c

Probability of complement of A =

P(A’) = 1 - P(A)

Mutually Exclusive Events (Disjoint)

Cannot occur at the same time

Joint Probability

Probability of the intersection of two events

P(A^B)

Probability of A and B

P(AUB)

Probability of A or B

P(B|A)

Probability of B given A (Conditional probability)

Multiplication Rule

P(A^B) = P(A) * P(B|A)

Conditional Probability Rule

P(B|A) = P(A^B)/P(A)

How do you know if events A and B are independent?

They are independent only if by knowing whether or not Event A has occurred (or will occur) doesn’t change the probability that Event B will occur.

What are some equations that help prove the independence of events?

P(A|B) = P(A)

P(A|B’) = P(A)

P(A^B) = P(A) * P(B)

Union of Events

The probability that A or B (or both) will occur

Addition Rule

P(AUB) = P(A) + P(B) - P(A^B)

Random Vars

They are numerical outcomes of random behavior (represented with capital letter)

Example of Random Var

X = # of children in a randomly selected household

Discrete Random Var

Can only take a countable number of values (X = num of children in randomly selected household)

Continuous Random Var

Can take on an infinite # of values (W = time it takes to run a mile)

Probability Distribution

Display of entire set of values with their associated probability.

Describing a probability distr.

• Shape

• Center (median)

• Spread (common to use SD but can use range)

• Can make histogram for shape (ex: skewed)

Mean of a Random Var

Take the sum of each x value times the probability of each x value

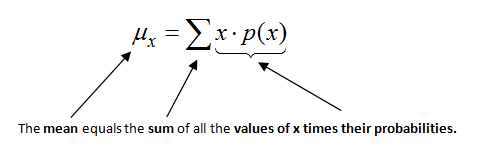
Interpreting Mean

In the long run, if many prairie dogs are randomly selected, the average # of pups per litter will be about 2.66 pups.

Standard Deviation of Random Var

The sum of (each x val - mean)² times P(x val))

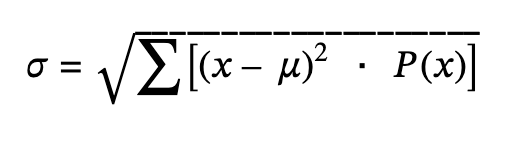
Interpret SD

The number of prairie dog pups in randomly selected litters will generally vary form the mean of 2.66 pups by about 1.267 pups.

Standard deviation is the ______ ____ of the variance.

square root

When a question asks you to calculate/interpret the expected value for something they mean…?

Find the mean!

Interpretations of random variable parameters should use appropriate ____ + include _____ of the population.

units, context

Transforming Mean of Random Var

a + b(mean)

Transforming SD of Random Var

|b|(mean)

Binomial Setting

• Two possible outcomes (success, fail)

• Independent trials of same random process

• Fixed # of trials, n

• Each trial has the same probability of success

Independent trials

Knowing that one outcome doesn’t help us to predict another outcome

Binomial Random Var

Random variable in binomial setting

What are two ways that you can find probabilities using binomial random variables?

• Use simulation to estimate probabilities

• Use the binomial probability formula to calculate probabilities

Binomial probability formula

(n combination x) (p^x)(1-p)^n-x

n = number of trials

p = probability

Calculator Function for Combination

MATH, PRB, nCr

Binompdf/Binomcdf

2nd, DISTR

Difference between cdf and pdf

Pdf finds exact probability at x = # while cdf finds cumulative probability up to x = #

Mean of binomial random var

mean = np

SD of binomial random var

SD = sqr(np(1-p))

Interpret mean of bin rando var

In many random samples of 40 cell phone owners, the BTB team can expect an avg of 8.4 people to have a cracked cellphone screen.

Interpret SD of bin rando var

In many random samples of 40 cell phone owners, the number with cracked phones will typically vary from the mean of 8.4 by about 2.58 phones.

Geometric Setting

• Two possible outcomes

• Independent trials

• Each trial has same probability of success

• BUT there isn’t a fixed # of trials!

Geometric distribution formula

P(X=x) = ((1-p)^x-1)(p)

Mean of geo distr

1/p

SD of geo distr

sqr(1-p)/p

Interpret geo mean

Over many seasons, we expect it will take 2.44 storms on average to get the first hurricane.

Interpret geo SD

Over many seasons the number of tropical storms it takes to get the first hurricane will differ by about SD from mean of ___.