Chapter 2: Chemistry and Measurements
1/32
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
33 Terms
International System of Units (SI)
Chemists use metric system and the International System of Units (SI), for measurement when they:
measure quantities
do experiments
solve problems
Volume
The space occupied by a substance
is measured using units of m³ in the SI system
is commonly measured in liters (L) and milliliters (mL) by chemists
is measured using a graduated cylinder in units of milliliters (mL)
Length
Measured in:
units of meters (m) in both the metric and SI systems
units of centimeters (cm) by chemists
Mass
The mass of an object, a measure of the quantity of material it contains,
is measured on an electronic balance
has the SI unit of kilogram (kg)
is often measured by chemists in grams (g)
Temperature
Temperature, a measure of how hot or cold an object feels,
is measured on the Celsius (°C) scale in the metric system
is measured on the Kelvin (K) scale in the SI system
is 18°Celsius or 64 °Fahrenheit on this thermometer
Time
Time is based on an atomic clock and is measured in units of seconds (s) in both the metric and SI systems
Useful relationships between units of mass include:
1 day = 24 hour
1 hour = 60 minutes
1 minute = 60 s
Measuring Tool
Used to determine a quantity such as the length or the mass of an object
Provides numbers for a measurement called measured numbers
Reporting Length
To report the length of an object,
observe the numerical values of the marked lines at the end of the object
estimate the last digit by visually dividing the space between the smallest marked lines
This estimated # is the final digit that is reported for a measured number
Reporting Length Example
Reporting Length: 4.55 cm
The metric ruler is marked at every 0.1 centimeter
You can now estimate that the length is halfway between the 4.5-cm and 4.6-cm marks and report the value as 4.55 cm
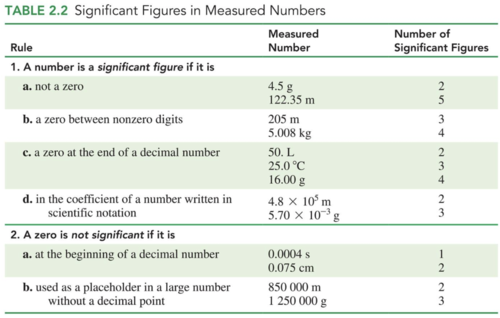
Significant Figures
In a measured number, the significant figures (SFs) are all the digits, including the estimated digit
All nonzero numbers are counted as significant figures
Zeros may or may not be significant, depending on the position in the number
Exact Numbers
Numbers obtained by counting items
Definitions that compare two units in the same measuring system

Calculated Answers
In calculations,
Answers must have the same number of significant figures as the measured numbers
Calculator answers must often be rounded off
Rounding rules are used to obtain the correct number of significant figures
Rules for Rounding Off
1) If the first digit to be dropped is 4 or less, then it and all following digits are simply dropped from the number
2) If the first digit to be dropped is 5 or greater, then the last retained digit is increased by 1
Rounding Off Calculated Answers
Rounding Off Calculated Answers:
When the first digit dropped is 4 or less, The retained numbers remain the same
To round 45.832 to 3 significant figures drop the digits 32 = 45.8 ▪
When the first digit dropped is 5 or greater, the last retained digit is increased by 1
To round 2.4884 to 2 significant figures drop the digits 884 = 2.5 (increase by 0.1)
Calculations with Measured Numbers
In calculations with measured numbers, significant figures or decimal places are counted to determine the number of figures in the final answer
Multiplication and Division with Measured Numbers
In multiplication and division, the final answer is written to have the same number of significant figures (SFs) as the measurement with the fewest SFs
2.8 (Two SFs) * 67.40 (Four SFs) / 34.8 (Three SFs) = 5.422988506 (Calculator display) = 5.4 (Answer, rounded off to two SFs)
Addition and Subtraction with Measured Numbers
In addition and subtraction, the final answer is written so that it has the same number of decimal places as the measurement having the fewest decimal places
2.045 (Thousandths place) + 34.1 (Tenths place, fewer decimal places) = 36.745 (Calculator display) = 36.1 (Answer, rounded off to the tenths place)
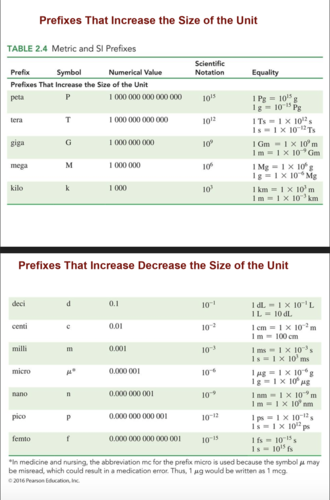
Prefixes
In the metric and SI systems of units, a prefix attached to any unit increases or decreases its size by some factor of 10.
The relationship of a prefix to a unit can be expressed by replacing the prefix with its numerical value.
1 kilometer (1 km) = 1000 meters
Metric and SI Prefixes
Measuring Length: Equalities
An equality shows the relationship between two units that measure the same quantity
For example, 1 meter is the same length as 100 centimeter or 1000 millimeter. The equality is written as:
P T G M k h da B d c m u n p f
P: Peta-
T: Tera-
G: Giga-M: Mega-
k: Kilo-
h: Hecto-
da: Deca-
B: BASE UNITS (meter, liter, gram, second, degree (Celsius)
d: Deci-
c: Centi-
m: Milli-
u: Micro-
n: Nano-
p: Pico-
f: Femto-
Measuring Volume
The cubic centimeter (cm³ or cc) is the volume of a cube with the dimensions:
1cm x 1cm x 1cm
Measuring Mass: Equalities
Equalities can be written for mass in the metric (SI) system
When metric equalities are used, 1 gram is the same mass as 1000 milligram and 0.001 kilogram
Writing Conversion Factors
Equalities:
use different units to describe the same quantity
can be between units of the metric system, between U.S. units, or between metric and U.S. units
Exact and Measured Numbers in Equalities
Equalities between units of:
The same system are definitions and use exact numbers
Different systems (metric and U.S.) use measured numbers and count as significant figures
Conversion Factors from a Percent, ppm (parts per million) and ppb (parts per billion)
A percent (%) is written as a conversion factor by choosing a unit and expressing the numerical relationship of the parts of this unit to 100 parts of the whole
For example, a person has 18% body fat by mass
Equality: 18 mass units of fat per 100 mass units of body mass
Problem-Solving Process
The problem-solving process begins by analyzing the problem in order to:
identify the given unit and needed unit
write a plan that converts the given unit to the needed unit
identify one or more conversion factors that cancel units and provide the needed unit
set up a calculation
Density
Density:
compares the mass of an object to its volume
is the mass of a substance divided by its volume

Sample Problem - Calculating Density: A 0.258-gram sample of high-density lipoprotein (HDL) has a volume of 0.215cm³. What is the density of the HDL sample?
Step 1) State the given and needed quantities
Given:
0.258g of HDL
0.215mL
Need:
Density (g/mL) of HDL
Connect:
Density expression
2) Write the density expression
D = M/V
3) Express mass in grams and volume in milliliters
Mass of HDL sample = 0.258 g
Volume of HDL sample = 0.215 mL
4) Substitute mass and volume into the density expression and calculate the density
D = 0.258g/0.215mL = 1.20g/1mL = 1.20g/mL
Sample Problem - Density of Solids in Water: What is the density (g/cm³) of 48.0 g of a metal if the level of water in a graduated cylinder rises from 25.0 mL to 33.0 mL after the metal is added?
1) State the given and needed qualities
Given:
48.0g
Volume of water = 25.0mL
Volume of water + metal = 33.0mL
Need:
Density (g/mL)
2) Plan out your calculations
Calculate the volume difference. Change to cm³, and place in density expression.
33.0mL - 25.0mL = 8.0mL
8.0mL * 1cm³/1mL = 8.0cm³
3) Set up the problem
Density = 48.0g/8.0cm³ = 6.0g/1cm³ = 6.0g/cm³
Sink or Float?
In water,
Ice floats because the density of ice is less than the density of water
Aluminum sinks because its density is greater than the density of water.
Density as a Conversion Factor
Density can be written as an equality:
For a substance with a density of 3.8g/mL, the equality is:
3.8g = 1mL
From this equality, two conversion factors can be written for density:
Conversion factors: 3.8g/1mL and 1mL/3.8g
Sample Problem - Using Density as a Conversion Factor: Greg has a blood volume of 5.9 qt. If the density of blood is 1.06 gram/mL, what is the mass, in grams, of Greg’s blood?
Step 1) State the given and needed quantities
Given:
5.9qt of blood
Need:
grams of blood
Connect:
U.S. - metric conversion factor
Density conversion factor
Step 2) Write a plan to calculate the needed quantity
quarts (U.S.-metric factor) milliliters > (Density factor) grams
Step 3) Write the equalities and their conversion factors including density
1qt = 946.4mL
946.4mL/1qt and 1qt/946.4mL
1mL of blood = 1.06g of blood
1.06g blood/1mL blood and 1mL blood/1.06g blood
Step 4) Set up the problem to calculate the needed quantity
5.9qt blood (Two SFs) x 946.4mL (Four SFs)/1qt (Exact) x 1.06g blood (Three SFs)/1mL blood (Exact) = 5900g of blood (Two SFs)
Specific Gravity (s p g r)
Relationship between the density of a substance and the density of water - compares the density of a substance to the density of water
Calculated by dividing the density of a sample by the density of water, which is 1.00 gram/milliLiter at 4 °Celsius
Example: A substance with a specific gravity of 1.00 has the same density as water (1.00 gram/milliLiter)