Geometry Brain Dump – Second Semester

Flashcards for Geometry Brain Dump - Second Semester

Right Triangles and Trigonometry Relationships

𝑠𝑖𝑛 (𝐴) =𝑐𝑜𝑠 (𝐵) , 𝑐𝑜𝑠 (𝐴) =𝑠𝑖𝑛 (𝐵) , 𝑡𝑎𝑛 (𝐴) = 1 𝑡𝑎𝑛 (𝐵)

Cavalieri's Principle for Three-Dimensional Solids

If every plane parallel to the two bases of two solids results in cross sections of equal area and the two solids have congruent altitudes, then the solids have equal volumes.

Population Density Formula

D=Population/Area

Shape resulting from 360° Rotation of a Rectangle

Cylinder

Shape resulting from 360° Rotation of a Triangle

Cone

Shape resulting from 360° Rotation of a Semi-Circle

Sphere

Angle formed by 2 Secants/Tangents

Measure of angle formed = 1/2(larger arc – smaller arc)

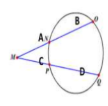
Tangent and Secant Formula

𝐴²= 𝐵(𝐵 + 𝐶)

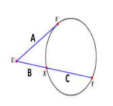
2 Secants Formula

𝐴(𝐴 + 𝐵) = 𝐶(𝐶 + 𝐷)

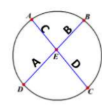
2 Chords Formula

(𝐴)(𝐵) = (𝐶)(𝐷)

2 Tangents

A=B

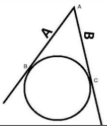
Area of a Sector

𝐴 = (θ/360)𝜋𝑟², where θ represents the central angle in degrees

Arc Length

Arc Length= 2𝜋𝑟(θ/360), where θ represents the central angle in degrees

Equation of circle with center at origin

𝑥² + 𝑦² = 𝑟²

Equation of a circle with center (ℎ, 𝑘)

(𝑥 − ℎ)² + (𝑦 − 𝑘)² = 𝑟²

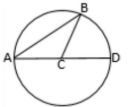
Inscribed Angle

∡𝐵𝐶𝐷 = 2∡𝐵𝐴𝐶

Angle Inscribed in a Semi-Circle

∡𝐴𝐵𝐷 = 90°

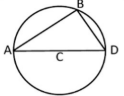
Inscribed Quadrilateral Theorem

The opposite angles of an inscribed quadrilateral to a circle are supplementary.

Cross Section of Cylinder (Horizontal, Vertical Plane)

Circle, Rectangle

Cross Section of Cone (Horizontal, Vertical Plane)

Circle, Triangle

Cross Section of Rectangular Prism (Horizontal, Vertical Plane)

Rectangle, Rectangle

Cross Section of Triangular Prism (Horizontal, Vertical Plane)

Triangle, Rectangle

Cross Section of Sphere (Horizontal, Vertical Plane)

Circle, Circle

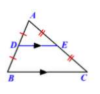
Triangle Midsegment Theorem

If 𝐴𝐵 = 𝐷𝐵 and 𝐴𝐸 = 𝐸𝐶, then 𝐷𝐸 ∥ 𝐵𝐶 and 𝐷𝐸 = 1/2𝐵𝐶.

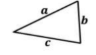
Triangle Inequality Theorem

𝑎 + 𝑏 > 𝑐 , 𝑎 + 𝑐 > 𝑏 , 𝑏 + 𝑐 > 𝑎