Heat Capacity

Molar Heat Capacity at Constant Volume

The amount of heat required to raise the temperature of 1 mole of a substance by 1 K at constant volume.

C_V = (1/n)(Q/ΔT)

Mathematical representation of Molar Heat Capacity at Constant Volume

Q = n(C_V)ΔT

Q = ?

Constant-Volume Heating (Ideal Gas)

At constant volume, the gas does no work (W = 0), so any heat added changes only the internal energy

ΔEint = Q (at constant V)

Mathematical representation of the Constant-Volume Heating (Ideal Gas)

Eint = (3/2)(nRT)

Internal Energy of a Monoatomic Ideal Gas

ΔEint = (3/2)(nRΔT)

Change in the Internal Energy (Monoatomic Ideal Gas, Constant C_V)

From ΔEint = Q = n(C_V)ΔT and ΔEint = (3/2)(nRT): C_V = (3/2)R

Molar Heat Capacity of a Monoatomic Ideal Gas at a Constant Volume

(3/2)R

(i)

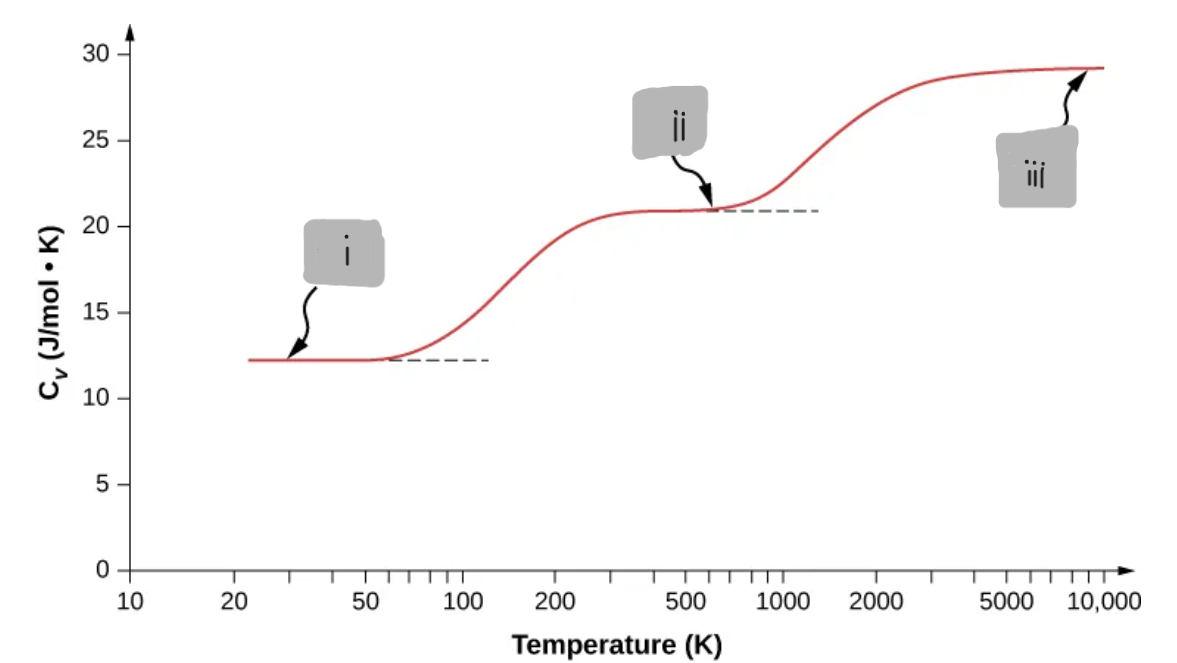
(5/2)R

(ii)

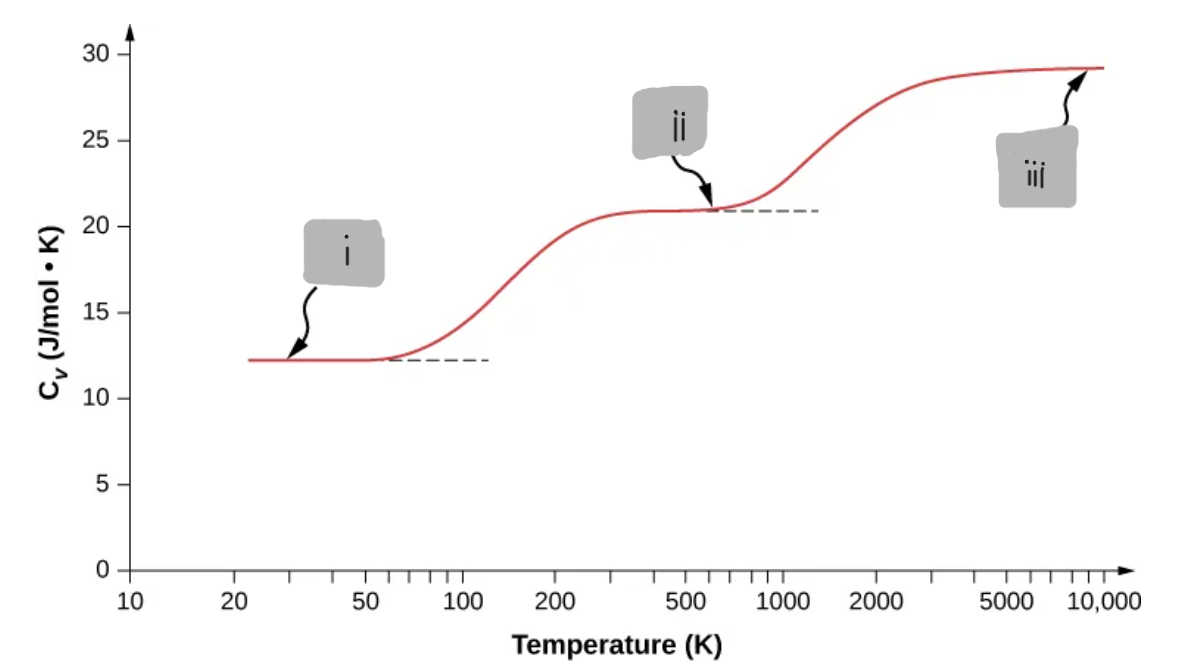
(7/2)R

(iii)

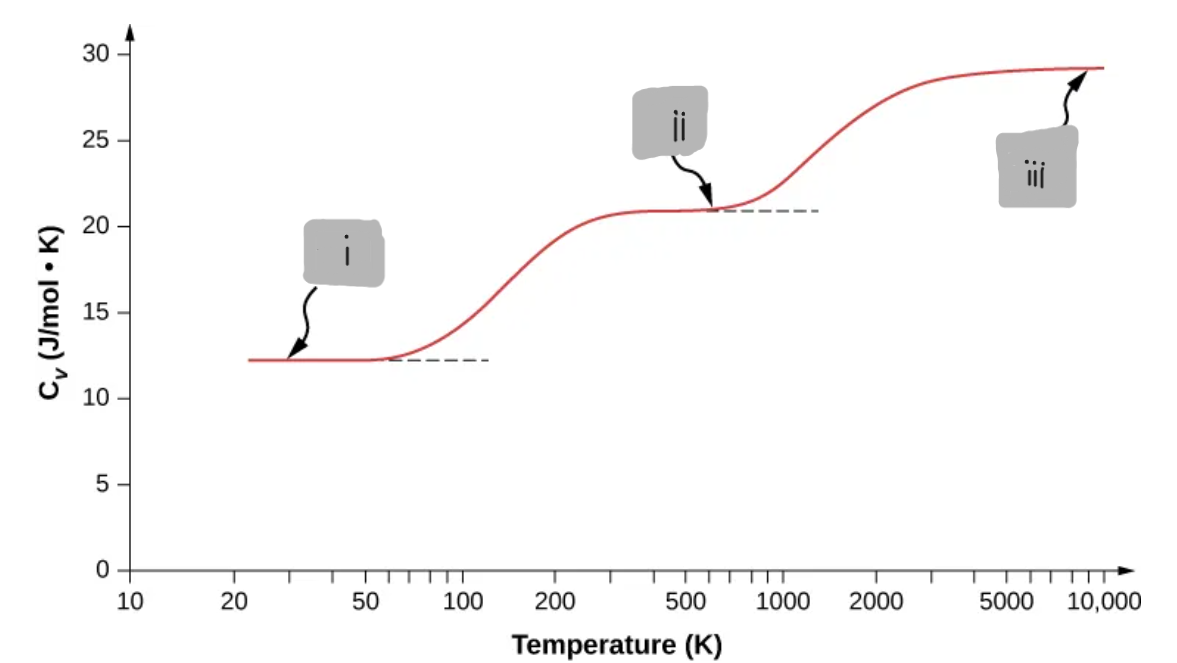
Degree of Freedom (d)

• An independent possible motion of a molecule that store energy

• e.g., translation and in x, y, z; rotation; vibration

3

A monoatomic gas has _ translational degrees of freedom (motion along x, y, z).

K̅ = (1/2)mv̅^2 = (3/2)(k_B)T

Average Translational Kinetic Energy (per molecule)

As (1/2)(k_B)T contributed by each of the 3 translational degrees of freedom

Average Translational Kinetic Energy (per molecule) can also be seen as what?

C_V = (d/2)R

Molar Heat Capacity in Terms of Degrees of Freedom for an ideal gas with d active degrees of freedom.

Equipartition Theorem

• In classical thermodynamics, at thermal equilibrium,

• energy is shared equally among all active degrees of freedom

• Each degree contributes (1/2)(k_B)T per molecule to the internal energy

• C_V = (d/2)R

• for an ideal gas

E_int = (d/2)nRT

Internal energy of an Ideal gas with d degrees of Freedom

Degrees of Freedom in a Diatomic Molecule (Classical View)

• 3 translational (x, y, z)

• 2 rotational (around axes perpendicular to bond axis)

• 2 vibrational (1 kinetic + 1 potential along the bond)

• Total classical: d = 7

Quantum Activation of Degrees of Freedom (Diatomic Gas)

Due to quantum mechanics, we know that not all degree of freedom are active at a given temperature. They “turn on” in steps as temperature increases.

Diatomic Gas at Very Low Temperatures (<~60K)

• Only translational motion is active

• d = 3

• C_V = (3/2)R

• Behaves like a monoatomic gas

Diatomic Gas at Room Temperature (≈ 300 K to ≈ 600 K)

• Translations + rotations active

• Vibrations are mostly frozen out

• d = 5

• C_V ≈ (5/2)R

Diatomic Gas at Very High Temperatures (≈ 3000 K and above)

• Translations + rotations + vibrations

• All are active

• d = 7

• C_V ≈ (7/2)R

Polyatomic (Nonlinear) Gas at a Typical Room Temperature d

• Usually has 3 translational motion + 3 rotational degrees of freedom active

• d ≈ 6

• C_V ≈ 3R

• Additional Vibrational modes become active only at higher temperatures

diatomic, polyatomic

For _________ and __________ gases, C_V depends on temperature, because different degrees of freedom become active at different temperatures (step-like behavior)

Spring Model of a Solid

Atoms in a solid can be modeled as masses connected by springs to neighboring atoms, allowing vibrations in x, y, and z.

Degree of Freedom for an Atom in a Solid

Each atom has:

• 3 kinetic (vibrations along x, y, z)

• 3 potential (spring potential in x, y, z)

• Total: d = 6

C_V = (d/2)R = (6/2)R = 3R

Predicted Molar Heat Capacity of a Solid (Equipartition) using d = 6

Law of Dulong and Petit

• Empirical rule stating that many solid elements have

• Molar Heat capacities close to C_V ≈ 3R

• at ordinary temperatures,

• Consistent with the 6 degrees of freedom per atom in the spring model

Limitations of Dulong-Petit Law

It fails at low temperatures and for some light elements (like Be and C) also it fails for some heavier metals, because quantum effects reduce the number of active degrees of freedom.