Proofs: Theorems, Postulates, Vocab

Trichotomy Law

For every real number, x,y only one is true

x > y, y > x, y=x

RAT

Right angle theorem: If two angles are right angle, then they are congruent

AAP

Angle Addition Postulate: Two angles that share a vertex are equal to their sum

Adjacent Angles

Two angles that share the same vertex and a common side

Complementary Angles DFN

Two angles whose sum is 90 degrees. Each angle is the complement of the other

Supplementary Angles DFN

Two angles whose sum is 180. Each angle is the supplement of the other

Linear Pair DFN

Two adjacent angles that form a straight angle/line

Vertical Angles DFN

Two angles formed by two sets of opposite rays (pair of lines)

VAT

Vertical Angles Theorem: Vertical Angles are Congruent

Supplement Theorem

If angles are supplementary to same angles or congruent angles, then they are congruent

Complement Theorem

If angles are complementary to same angles or congruent angles, then they are congruent

Linear Pair Theorem

A linear pair is supplementary

SAP

Segment Addition Postulate: : Two segments that are colinear are equal to their sum

Angle Bisector DFN

A ray, segment, or line that divides an angle into two congruent angles

Angle trisector DFN

Two rays, segments, or lines that divide an angle into three congruent angles

Midpoint DFN

A point that divides a segment into two congruent segments bisects the segment

SSS

Side-Side-Side Posulate

Radii Therom

All radii are equal

Circle DFN

A set of points that are equidistant from a fixed point(the center)

CPCTC

Corresponding parts of congruent triangles are congruent

SAS

Side-Angle-Side Postulate

ASA

Angle-Side-Angle

Median Definition

A line segment drawn from any vertex of the triangle to the midpoint of the opposite side.

Altitude of a Triangle Definition

A line segment drawn from any vertex of the triangle perpendicular to the opposite side. (height)

Auxiliary Lines

Lines, rays, or segments that are drawn on a figure to be able to solve the problem

Line Postulate

Two points determine a line (ray or segment)

Scalene Triangle DFN

Triangle with no congruent sides

Isosceles Triangle DFN

Triangle with at least two congruent sides

Equilateral Triangle DFN

Triangle with three congruent sides

AAS

Angle-Angle-Side Postulate: If two angles and the non-included angle of one triangle are congruent to the corresponding angles and side of another triangle, then the triangles are congruent

HL

Hypotenuse-Leg Postulate: If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and leg of another right triangle, then the triangles are congruent

ITT

Isosceles Triangle Theorem: If two sides of a triangle are congruent, then angles opposite the sides are congruent

CITT

Converse of Isosceles Triangle Theorem: If two angles of a triangle are congruent, then the side opposite the angles are congruent

Midpoint Formula

(x1 + x2)/2, (y1 + y2)/2

PBT

Perpendicular Bisector Theorem: If a point is on the perpendicular bisector of a segment, then it is equidistant from the end points of the segment.

PBTC

Perpendicular Bisector Theorem Corollary: If two points are each equidistant from the endpoint of a segment, then the two points determine the perpendicular bisector of that segment.

SCAR

Supplementary Congruent Angles are right

Side Splitter Therom

If a line is parallel to one side of a triangle and it intersects the other two sides, it divides those two sides proportionally

Parallel Lines Proportional Parts Therom

If three or mores parallel lines intersect two transversals, then they cut the transversals proportionally

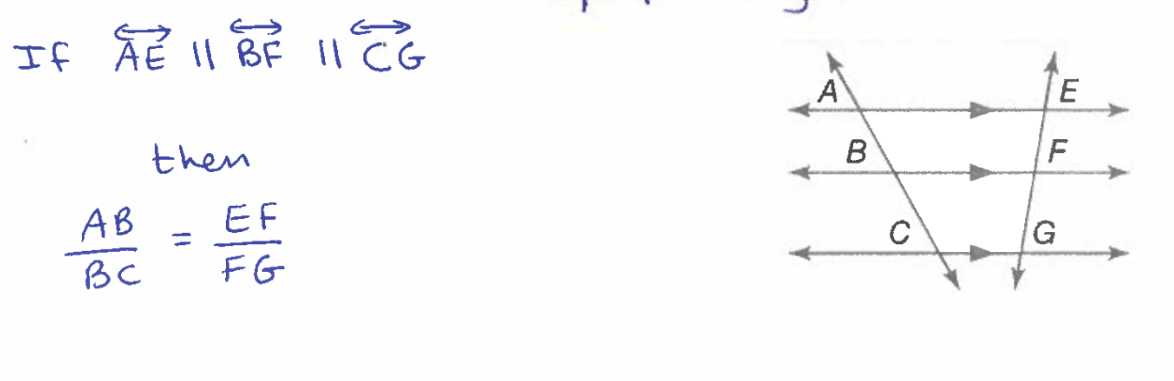
Median of a Trapeziod Definition

A line that connects opposite midpoints and is parallel to the bases

Angle Bisector Therom

If a ray (or segment) bisects an angle of a triangle, it divides the opposite side into segments taht are proportional to adjacent sides

CSSTP

Corresspondng Sides of Simliar Triangles are Proportional

Similar Figures Theorem

If two figures are similar, than the ratio of their areas equals the ratio of corresponding segments (scale factor)