9 - differentiation

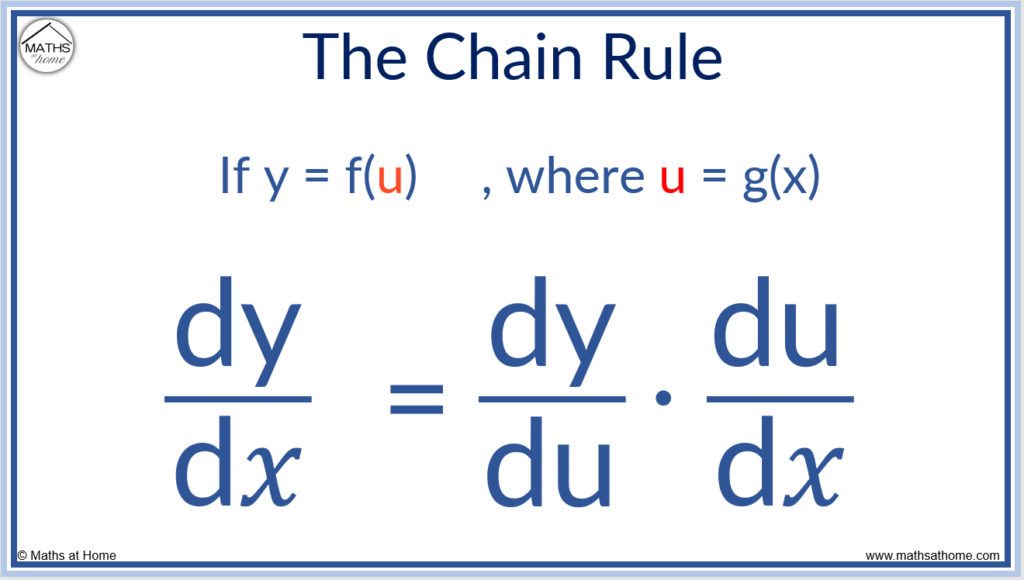
what is the chain rule

dy/dx = dy/du x du/dx

where y is a function of u
and u is a function of x

example of the chain rule: differentiate y = (2x + 4)³

1. define u and y

let u = 2x + 4
let y = u³

2. differentiate both

du/dx = 2
dy/du = 3u²

3. use the chain rule - multiply them

dy/dx = 6u²

4. replace u so its all in terms of x

dy/dx = 6(2x+ 4)²

easier way of thinking of the chain rule

differentiate the bracket then times it by the derivative of what’s in the bracket

(2x + 4)³ —> 2 × 3(2x + 4)² —> 6(2x + 4)²

what’s the quotient rule

works when y = f/g

works when f and g are functions of x

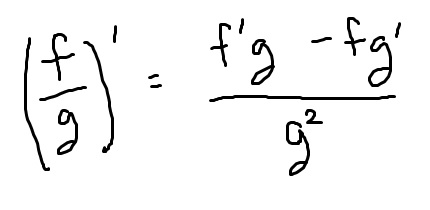
what’s the product rule

when y = fg

when f and g are functions of x

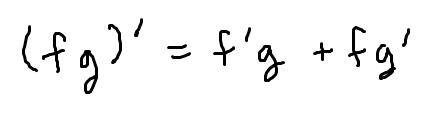
when you are differentiating angles and trigonometry, what do you HAVE to do

use RADIANS

differentiate y = sinx

dy/dx = cosx

differentiate sinx from first principles

1. write it out in first principles equation (swap ‘f’ for ‘sin’)

2. use addition formula to rewrite ‘sin(x+h)’

3. group the terms involving sin x and cos x (factorise)

4. set the limit for h as going to 0

5. use small angles to rewrite ‘sinh’ and ‘cosh' (just learn them don’t bother with why)

6. evaluate it with the new ‘0’ and ‘1’ you got from step 5

how do you differentiate y = sinf(x) or y = f(sinx)

use the chain rule!

differentiate y = cosx

dy/dx = -sinx

(the negative is VERY important)

differentiate cosx from first principles

1. write it out in first principles equation (swap ‘f’ for ‘cos’)

2. use addition formula to rewrite ‘cos(x+h)’

3. group the terms involving cos x (factorise)

4. set the limit for h as going to 0

5. use small angles to rewrite ‘sinh’ and ‘cosh' (just learn them don’t bother with why)

6. evaluate it with the new ‘0’ and ‘1’ you got from step 5

how to differentiate y = cosf(x) or y = f(cosx)

use the chain rule!!

differentiate y = tanx

dy/dx = sec²x

proof for differentiating tanx

1. rewrite tanx as sinx/cosx

2. use the quotient rule

3. use trig identities to make the numerator 1

4. 1/cos² = sec² as req.

how to differentiate y = tanf(x) or y = f(tanx)

use the chain rule

differentiate y = e^f(x)

dy/dx = f’(x)e^f(x)

similar vibes to the chain rule

reciprocal rule

dy/dx = 1/dx/dy

use when you have to differentiate something in terms of y

differentiate y = lnx

dy/dx = 1/x

differentiate y = ln[f(x)]

dy/dx = f’(x)/f(x)

(derivative over original function)

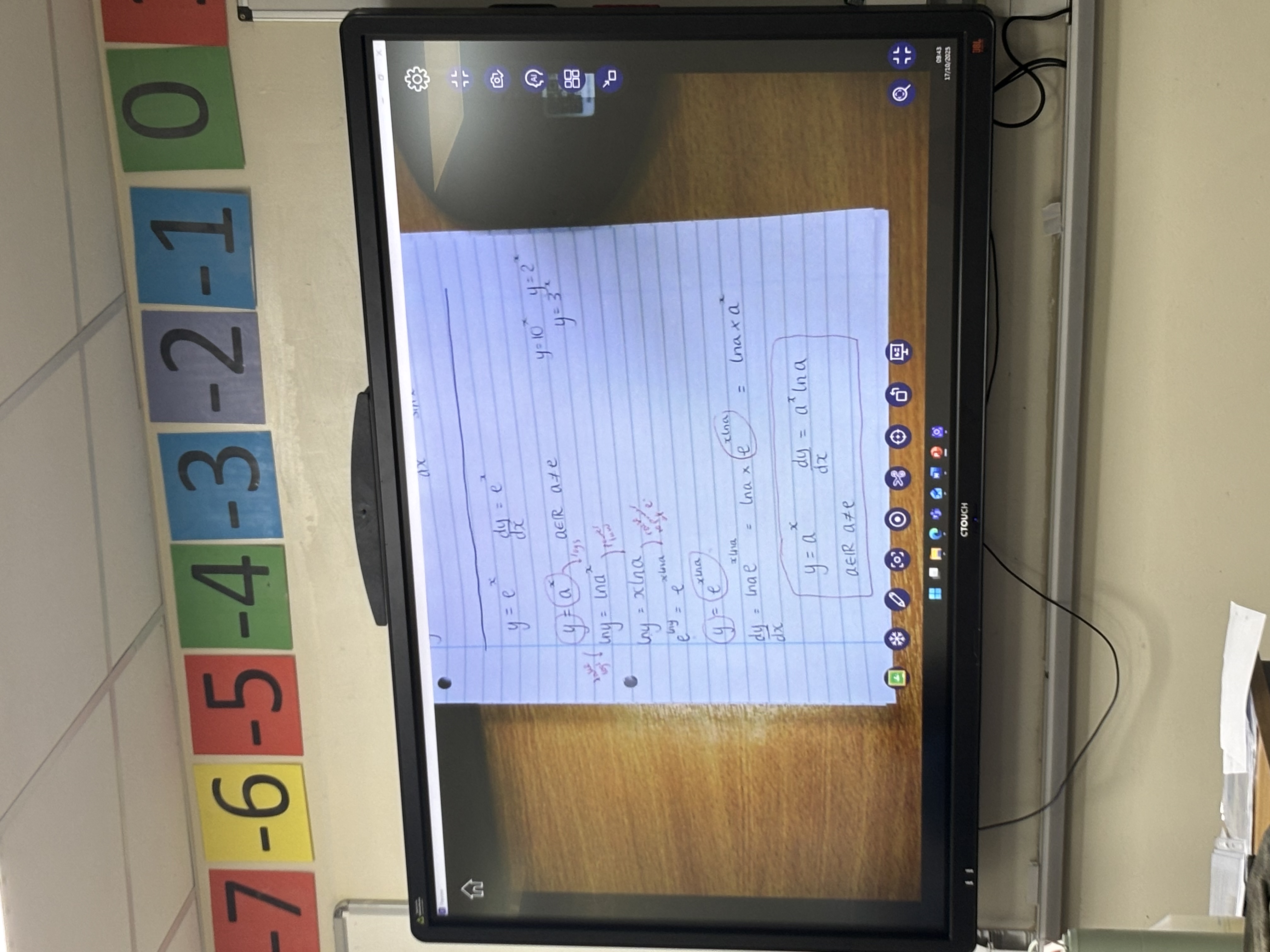
how to differentiate exponentials with no e

the rule is as follows (in the picture)

so if y = a^x 
then dy/dx = a^xlna

differentiate cosec x

-cotxcosecx

proof for differentiating cosec x

1. rewrite as 1/sinx

2. rewrite as (sinx)^-1

3. differentiate using the chain rule

   1. rewrite to get the answer we have

differentiate cotx

cosec²x

differentiate secx

secxtanx

proof for differentiating cot and sec

same concept as cosec

differentiate arcsinx

.

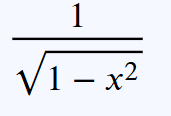
differentiate arccosx

.

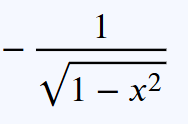
differentiate arctanx

.

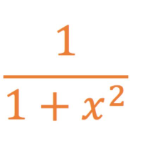
where can you find the derivatives of arcsin, arccos, and arctan

the FM section of your booklet

how to differentiate a function of y with respect to x

differentiate as normal

then multiply by ‘dy/dx’

eg. y² —> 2y(dy/dx)

how can derivatives be connected

like fractions

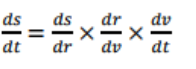
where and what is a point of inflection

what: where the function goes from concave to convex or vice versa

where: when y’’ = 0 

what to be careful with with POIs

y’’=0 is not always a poi so check 0.01 to either side of it to check if there is a change in concavity or not

what can we use the chain rule for also

parametric differentiation

how does parametric differentiation work

dy/dx = dy/dt x dt/dx

so if u differentiate both of the equations in the parametric, then flip one around, you’ll have your dy/dt and dt/dx so you can find dy/dx (it would be in terms of t)

do u always have to parametrically differentiate parametric eq.s

no if its easier to do the cartesian version then u can

but both are valid options just do the easiest