CSE 4830 - Computer Vision

computer vision is an ____ field whos goal is to enable machines to automatically ____ and ____ visual information

multidisciplinary, interpret, understand

Computer vision focuses on visual information from the _____ world.

real

Computer vision aims to help computers _____ visual data rather than just ____ it.

interpret, display

In computer vision, understanding is NOT just seeing _____.

____ _____ in images is a key part of visual understanding.

Understanding how things move involves interpreting _____.

pixels, recognizing objects, motion

Interpreting the overall environment of an image is called ____ _____.

scene understanding

Computer vision systems can make decisions based on ____ ____

visual input

Extracting physical information from images often involves _____ and ____ .

geometry, motion

Determining where an object is over time is called ____ _____.

object tracking

Estimating how fast and in what direction an object is moving is called _____ _____.

motion estimation

Determining how far away objects are is called _____ _____.

depth estimation

Computer vision attempts to infer _____ structure from _____ images.

3d, 2d

Identifying whether something is a person, dog, or chair is an example of ____ _____.

object recognition

Recognition uses _____ and _____ to interpret images.

algorithms, representations

Mining visual data involves working with large image or video _____.

datasets

Vision is considered an _____ problem.

inverse

In an inverse problem, we try to infer the _____ from the ____ ____.

cause, observed result

What are the steps in the computer vision pipeline?

image acquisition, preprocessing & enhancement, feature extraction, object recognition, interpretation & decision making

We can think of a greyscale image as a function:

f: {R}² → {R}

• input= ___ ___ ___

• output = ____

spatial location (x,y), intensity

A digital image is a ____ version of the continuous image where..

image plane = a ____

each entry = ____ ____

discrete, matrix, pixel intensity

pixel values:

0 is ___ and 255 is ___

black, white

a scalar is just a ____

number

how do you denote a scalar?

lowercase, italics

a vector is a ____ ____ of numbers

1d array

how do you denote a vector?

lowercase, italics, bold

a matrix is a ___ ___ of numbers

2d array

how do you denote a matrix?

uppercase, italics, bold

a 0D tensor is a ____. a 1D tensor is a ____, a 2D tensor is a ____, a 3D+ tensor is a ____

scalar, vector, matrix, tensor

a grayscale image is a ____ tensor

2d

a RGB image is a ____ tensor

3d

whats the transpose of a scalar?

itself

a transpose swaps ___ and ___

rows, columns

matrix addition (element wise) the matrices must be the ___ ___

same size

what do you do when you multiply a MATRIX by a SCALAR?

scale all entries

what do you do when you add a SCALAR to a MATRIC

shift all entries

matrix times a matrix: row of ___ times the column of ___ AND ___ ____ ___

1st, 2nd, dimensions must align

the result of the inner product (dot product) of two vectors is a….

scalar

the outer product of two vectors is a….

matrix

norms are functions that measure how __ a __ is

large, vector

norms are the distance from the ___ ___ to the ___

zero vector, vector

positive definiteness: the unit vector with size 0 is the __ ___, and NO OTHER VECTOR can have ___ ___

zero vector, zero length

absolute scalability: scaling a vector scales its length by the __ __ of a scalar, _ doesnt matter only _

absolute value, direction, magnitude

unit vector: vector with a norm equal to _

1

unit vector represents _ only, not _

direction, magnitude

orthogonal vectors: two vectors whose __ ___ is __

dot product, zero

orthogonal vectors: vectors are _

perpendicular

symmetric matrix: a matrix equal to its _

transpose

symmetric matrices are only possible for __ matrices

square

orthogonal matrix: the __ of a square matrix equals its _

transpose, inverse

orthogonal matrix: columns and rows are _

orthonormal

diagonal matrix: all __ ___ entries are __

off diagonal, zero

diagonal matrix: diagonal entries cant be _

zero

eigendecomposition is a way to break a matrix into:

• __ it acts along (eigenvectors)

• __ ___ it acts along each __ (eigenvalues)

directions, how strongly, direction

A non-zero vector v is an eigenvector of matrix A if:

___

Av = lambda v

The scalar λ\lambdaλ represents the __________ factor applied to the eigenvector.

scaling

Multiplying a matrix by its eigenvector does not change the ___, only the ___

direction, magnitude

Geometric Meaning

• eigenvectors are __ that stay the same after transformation

• eigenvalues tell how much — or —- occurs

directions, stretching, compressing

eigenvectors must be __

eigenvalues are __

non-zero, scalars

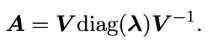
A ___ matrix can be written as.

• V = matrix of __________

• Λ\LambdaΛ = diagonal matrix of __________

diagonalizable, eigenvectors, eigenvalues

Real Symmetric Matrix:

A = A^T

• Eigenvalues are __

• Eigenvectors can be __

real, orthonormal

SVD works for —- — matrices

any size

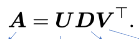
SVD equation:

U = output __

V = input __

D = __ values

directions, directions, singular

pseudoinverse is used when the normal inverse — — —

does not exist

trace is a — of — —

sum, diagonal elements

trace equals sum of —

eigenvalues

determinant = product of —

measure — —

eigenvalues, volume scaling

If det(A) ≠ 0 → matrix is __________
If det(A) = 0 → matrix is __________

invertible, not invertible

orthonormal vectors are — to eachother and — —

perpendicular, unit length

unit length is a length of —

1

probability theory allows us to — in the presence of —

reason, uncertainty

information theory allows us to — the amount of —

quantify, uncertainty

There are - interpretations of uncertainty

two

frequentist interpretation (of probability)

probability is defined as a - - -

P(a) is the - of an - a in the limit

Example: coin toss, probability based on how often heads appears over many trials

long run frequency, frequency, event

subjective interpretation (Bayesian, of probability)

probability represents a - - -

P(a) reflects how strongly we - a will occur

Example: - -

degree of belief, believe, doctors diagnosis

a probability space describes a - - or - and consists of 3 components

1. Sample space

• Ω is the set of - - -

2. Set of events (S)

• an event is a subset of the - -

• An event may include: 0 to - outcomes

3. Probability Distribution(D)

• P is a function that assigns - to - or -

• Probabilities are real numbers between - and -

• The probability of an event is the sum of the probabilities of its -

random process, event, all possible outcomes, sample space, N, probabilities, outcomes, events, 0, 1, outcomes

what are the 3 components of a probability space?

sample space, set of events, probability distribution

what are the two types of probability space

discrete probability space, continuous probability space

types of probability space:

discrete:

• Ω is -

• analysis involves -

continuous:

• Ω is -

• analysis involves -

finite, summation, infinite, integrals

Ω is the number/set of all - -

possible outcomes

A random variable - is a function that assigns a - value to each - of a random process

X, numerical, outcome w

how many types of random variables?

two

types of random variables:

categorical (discrete): takes values from a - -

continuous (real-valued): takes values from a - -

countable set, continuous range

a probability distribution describes how - each possible - of a - - is

likely, outcome, random process

PROPERTIES OF A PROBABILITY DISTRIBUTION

1. probabilities cant be -

2. normalization means that something must -

3. additivity: if two events cant both happen, — their —

negative, happen, add, probabilities

a probability mass function is used when outcomes are -

countable

the PMF is written as:

P(X=x)

PMF assigns a probability to each - - of a - - -

possible value, discrete random variable

PMF:

• must be between - and -

  • the sum must equal -

0, 1, 1

a probability density function is used when outcomes are -

continuous

PDF is defined as:

p(x)

PDF

• must be - than -

• integral must equal -

• does NOT have to be - - or equal to -

greater, 0, 1, less than, 1

for continuous variables. probability is computed as the - under the -

area, curve

a PMF assigns probability to - values, while a PDF assigns density to - values

discrete, continuous

multivariate probability distributions are used when more than one - - are involved

random variable

X = car model type

y = manufacturer

- - tells us how likely each combination is

joint probability

marginal probability asks: “What is the probability of - - of what - is?”

X regardless, Y

marginal probability: discrete case:

• fix -

• add up - over all - -

x, probabilities, possible y

to compute a marginal probability we - the other variable

ignore

marginal probability removes the - of other -

effect, variables

conditional probability answers: “What is the probability of -, - that - has already -?”

Y, given, X, happened

relationship between marginal & conditional probability:

• marginal uses the - -

• conditional uses - by a -

sum rule, division, marginal