Kin 483-Ch.8: The T-Test & Chi Square: Comparing Means From 2 Data Sets

Inferential Statistics

• Inferential: take a sample from a larger population and make a generalization about the population from it

  • researchers gather data on a sample and then desire to generalize to a population.

    • ex: local news:

      • “There they are again! The most terrifying five words in television.”

        “According to a NEW study…”

• Population: parameter

• Sample: statistics

Variable Classification

• Independent Variables: related to the dependent variable often used as a predictor

• Dependent Variables: the variable you are trying to predict (criterion variable

• Example: We want to predict the number of pull ups the class can do based on body weight

  • independent variable = body weight

  • dependent variable = # of pull ups

3 Types of Hypotheses

1. Research Hypothesis

2. Null Hypothesis

3. Alternative Hypothesis

*Statistical hypotheses

Research Hypothesis

• educated guess of what will happen

  • Ex: “Imagery is better for performance than no imagery”

Null Hypothesis

• statement that there is no relationship between two variables

  • Ex: “There is no difference in performance when using different mental strategies”

• Often the opposite of the research hypothesis

Alternative Hypothesis

• statement that there is a relationship; opposite of the null—what is believed if the null hypothesis is rejected

  • Ex: “The mean for group 1 and group 2 are not equal”

• Reflects what is stated in the research hypothesis

Hypothesis Testing: General Process

1. Research hypothesis of relationship

2. Statistical null hypothesis

3. Alternative hypothesis

4. Obtain data

5. Make decision based on probability

Hypothesis Testing: Setting the Alpha Level

• Before you can reject or accept a hypothesis you must select a probability level (alpha level)

  • Alpha Level: the probability of obtaining the statistic by chance

• Typical alpha levels:

  • p=0.05

  • p=0.01

Hypothesis Testing: Type 1 Error

• probability of making an incorrect conclusion

  • When the null hypothesis is true but it’s incorrectly rejected

• Possible causes of error:

  • measurement error

  • lack of random sample

  • investigator bias

Hypothesis Testing: Type 2 Error

• concluding no relationship between variables in a population when there truly is a relationship

  • When a hypothesis not true but is incorrectly accepted

• possible causes of error:

  • measurement error

  • lack of power (participants)

  • treatment application wrong

Statistical Tests

• Help us to determine associations or differences between groups;

  • are groups different from one another?

3 Types—Determined by # and nature of IV and DV:

1. Chi-Square

2. t-Test for Two Independent Groups

3. Dependent t-test for Paired Groups

What Analysis Do I Use?

Chi-Square:

• Independent Variable: 1 nominal

• Dependent Variable: 1 nominal

T-Test:

• Independent Variable: 1 nominal (2 groups)

• Dependent Variable: 1 continuous

T-Test Assumptions

1. Normal Distribution from the sample

2. Samples are randomly selected

3. Samples have equal variance

4. Data must be interval or ratio (parametric)

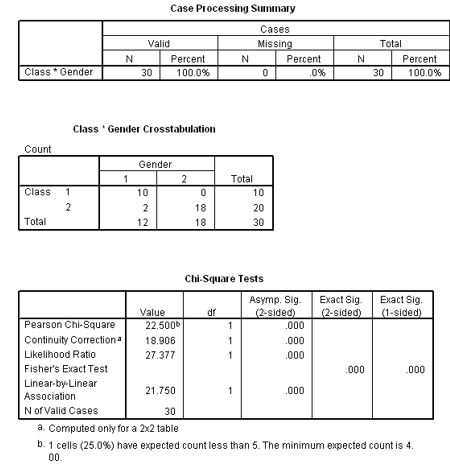
Chi Square Example

• “Gender Nominal data.xls”

• We want to find out if males and females enroll in aerobic dance and weight training classes equally

• Purpose of the Chi Square statistic – determine if there is an association between levels of one or more nominally scaled variables

Steps:

1. Import data

2. Analyze—> Descriptive Statistics —> Crosstabs

3. Rows: Class ; Columns: Gender

4. Click Chi Square—> Continue—> OK

Analysis:

• Middle Box = general summary (Class Gender Crosstabulation)

• Df=degrees of freedom

• Asymp.sig = significance

• Compare p-value with alpha level

  • in this case p< alpha

    • alpha: 0.05

    • p: 0.00

• If p < alpha, reject the null hypothesis

• if p > alpha, accept the null hypothesis

• TLDR: there are gender differences in enrollment in these classes

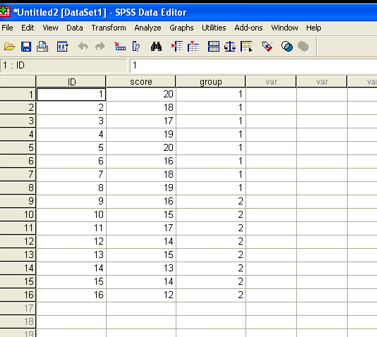
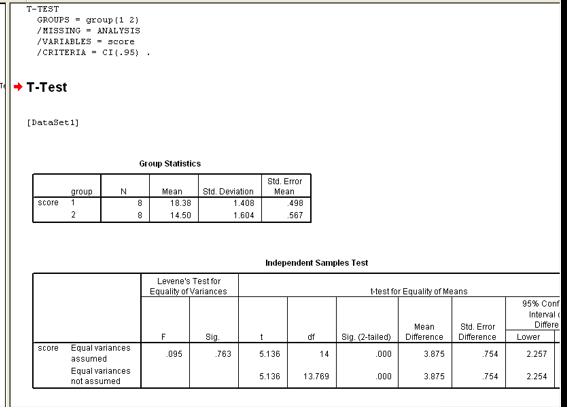
T-Test Example

• “Ch. 5 Volleyball continuous data.xls”

• We want to find out if there are serving accuracy differences between a junior varsity and varsity volleyball team

• Purpose of the t-Test for 2 independent samples – examine the difference in 1 continuous variable between 2 (only 2) independent groups (not related)

Steps:

1. Import Data

2. Analyze—> Compare Means —> Independent Samples T Test

3. Test Variable: Score

4. Define Groups: Group 1=1 (JV =1) , Group 2 = 2 (Varsity = 2 )

5. Continue —> Define Groups —OK

Analysis:

• Sig = p value

  • Large: = 0.763

• If p-value > 0.05, then Accept the null hypothesis (do not address the alternative)

• If p-value < 0.05, then Reject the null hypothesis

  • Varsity is better than JV

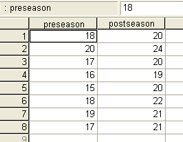
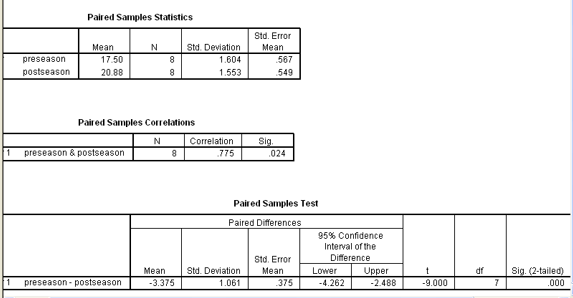
T-Test for Paired Groups Example

• “Jump data.xls”

• We want to find out if a jump training regimen is effective for basketball payers so we compare performance at the beginning and end of the season

• Purpose of the t-Test for paired groups – compare 2 related groups on 1 dependent variable; comparing siblings, comparing a team at the beginning and end of the season

Steps:

1. Import Data

2. Analyze—>compare means—> paired samples T-test

3. Paired Variables: preseason and postseason

4. OK

Analysis:

• strong correlation due to high significance (0.024)

• Sig (2-tailed) = p-value

• If p-value is < alpha, reject the null —- there is a significance