Indefinite Integration [MOSTLY COMPLETE]

study at your own risk

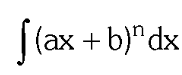
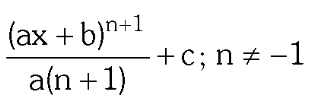
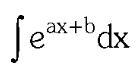
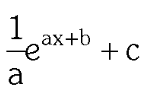
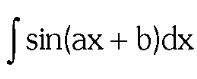
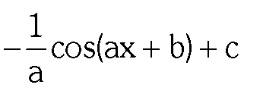
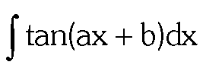
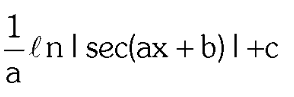
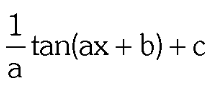
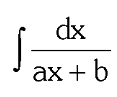
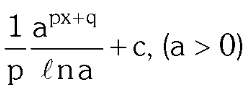
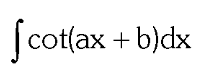
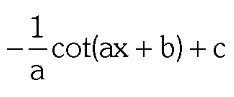
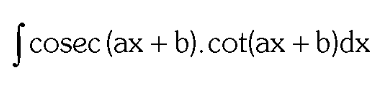
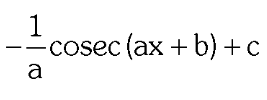
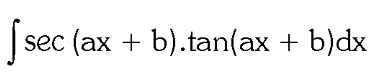
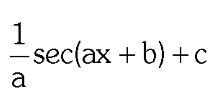
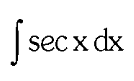
two forms

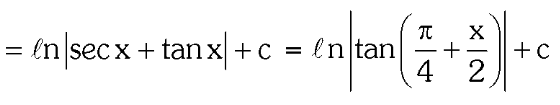
3 forms

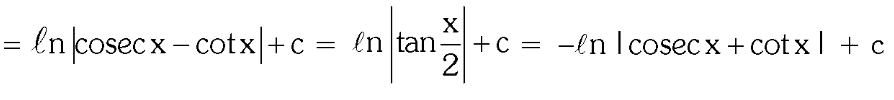
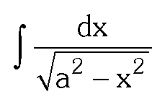
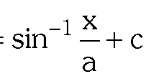
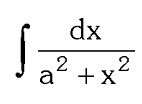
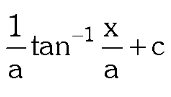
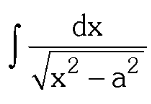
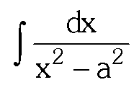
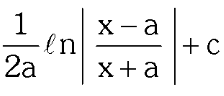
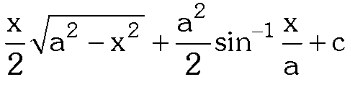
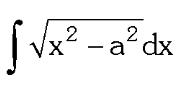
$$\int\dfrac{dx}{\sin²x \cos²x}$$

$$\tan x-\cot x +c$$

$$\int \sec²x\csc²x\ dx$$

$$=\int \sec²x+\csc²x\ dx$$

$$=\tan x - \cot x +c$$

What is the differentiation of $\int_{g(x)}^{f(x)}h(t)\ dt$?

$$h(f(x))(f’(x))-h(g(x))(g’(x))$$

$$\int\dfrac{f’(x)}{f(x)}dx$$

$$\ln|f(x)|+c$$

$\int g(x)\sqrt{f(x)}\ dx$ where $f(x)$ is a linear function

What do you take as $t$?

$$t= \sqrt{f(x)}$$

$$t²=f(x)$$

What substitution do you use for $a²+x²$?

$$x=a\tan\theta$$

What substitution do you use for $a²-x²$?

$$x=a\sin\theta$$

or

$$x=a\cos\theta$$

What substitution do you use for $x²-a²$?

$$x=a\sec\theta$$

What substitution do you use for $a+x$ or $a-x$?

$$x=a\cos2\theta$$

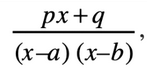
convert to partial fractions

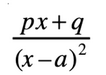
convert to partial fractions

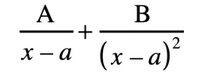
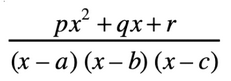
convert to partial fractions

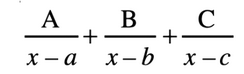
convert to partial fractions

convert to partial fractions

($x²+bx+c$ has imaginary roots)

How do you integrate a function where $\dfrac{f(x)}{g(x)}$ and the order of $f(x)$ is greater than or equal to order of $g(x)$?

Divide $f(x)$ by $g(x)$ and then separate into fractions, then use partial fractions / perfect square method

How will you factorize a 1/quadratic form where the quadratic is NOT factorisable?

turn the quadratic into a perfect square, then use substitution. Then use one of the given formulae.

How will you factorize a linear/quadratic form where the quadratic is NOT factorisable?

Differentiation method

Use $N=\lambda((D)’)+\mu$ to split the numerator into two.

for $\dfrac{\lambda((D)’)}{D}$ use substitution $t=D$ and for $\dfrac{\mu}{D}$ use perfect square method

How do you integrate a linear function $L$ that is wholly under square root (whether in numerator or denominator)?

Use substitution $L=t²$

How do you integrate a Quadratic function $\dfrac{1}{\sqrt{Q}}$ ?

do perfect square method

How do you integrate a Linear by Quadratic function $\dfrac{L}{\sqrt{Q}}$ ?

Use differentiation method then perfect square

How would you integrate a quadratic under square root $\sqrt{Q}$?

Use perfect square, then a given formula

How would you integrate a quadratic under square root multiplied by a linear or quadratic function $L\sqrt{Q}$ or $Q\sqrt{Q}$?

Use differentiation method, and then for the first one use substitution and for the second term use perfect square and formula

$$Q_1=\lambda(Q_2)+\mu((Q_2)’)+\sigma$$

How would you integrate a quadratic over root quadratic $\dfrac{Q}{\sqrt{Q}}$?

Use differentiation method, and then for the first one use substitution and for the second term use perfect square and formula

$$Q_1=\lambda(Q_2)+\mu((Q_2)’)+\sigma$$

How do you integrate a trigonometric function that is raised to an even power?

Use double-angle formula for square, convert others into powers of the square

How do you integrate a trigonometric function that is raised to an odd power?

separate one term out to make (trig function)^{even power} x (trig function), convert to 1-(trig function)² type, then use that new one as substitution sorry i can’t explain

If two trigonometric functions are multiplied together and both have some power $\neq$ 1, how do you integrate?

1. If both have odd powers, take any one of them out and solve

2. If only one of them has odd powers, take that one out and solve

3. If both of them have even powers, you’re unlucky. Convert to double-angles, multiply through.

How to integrate function where trigonometric ratios are multiplied together and have fractional powers?

try to make fractional powers whole number powers by multiplying and dividing with the right amount

sec²x and cosec²x desire to be dt carnally. got it?

yea

What’s the first step in integrating $\int \dfrac{\sin2x}{\sin^4x+\cos^4x}dx$?

convert $\sin2x$ to $2\sin x \cos x$

How would you integrate $\int \sec³x\ dx$?

$$=\int \sec²x\cdot \sec x\ dx$$

= $\int \sec²x\cdot \sqrt{1+\tan²x}\ dt$

How will you integrate forms like $\dfrac{1}{a\sin²x+b\cos²x+c\sin x\cos x+d}$?

divide through by $\cos²x$ and simplify. $sec²x$ will be $dt$.

How will you integrate when there is a trigonometric function with other constant term in denominator?

convert to half-angle form of tan. $\sec²x$ will be $dt$.

How will you integrate when there is form $\dfrac{1}{a\sin x+b\cos x}$?

convert into $\sin(A+B)$ and solve. final will be $\frac12 \int\csc(A+B) dx$.

How will you integrate when there is form $\dfrac{1}{a\sin x+b\cos x + c}$?

Convert them all into half angles like

$$\dfrac{1}{2a\tfrac{\tan\frac{x}{2}}{\sec²\frac{x}{2}} + b\tfrac{1-\tan²\frac{x}{2}}{sec²\frac{x}{2}} + c\tfrac{\sec²\frac{x}{2}}{\sec²\frac{x}{2}}}$$

How will you integrate $\dfrac{p\sin x+q\cos x+r}{a\sin x + b\cos x+c}$ form?

differentiation method

$N=\lambda(D)+\mu((D)’)+\sigma$ then it’s easy

how do you solve integrals that are in the form $\int \dfrac{trig\ x}{trig\ (x-a)}dx$?

let $(x-a)=t$ then substitute to make

$$\int\dfrac{trig\ (t+a)}{trig\ t}dt$$

Then expand the compound angle and cancel

How will you integrate $\dfrac{ae^x+be^{-x}}{ce^x+de^{-x}}$ form?

$$N=\lambda(D)+\mu((D)’)+\sigma$$

How will you integrate $\dfrac{1}{trig_1(x-a)\ trig_2(x-b)}$ form?

1. if $trig_1=trig_2$ then multiply and divide by $\sin(a-b)$ or $\sin(b-a)$ depending on options, take denominator outside of integral, and expand numerator ($\sin(a-b)=\sin((x-b)-(x-a)$) and cancel

2. If $trig_1\neq trig_2$ then multiply and divide by $\cos(a-b)$ or $\cos(b-a)$ depending on options, take denominator outside of integral, and expand numerator ($\cos(a-b)=\cos((x-b)-(x-a)$) and cancel

when you see $\int\dfrac{dx}{x^4+kx²+1}$ or $\int\dfrac{x²\ dx}{x^4+kx²+1}$ then what form are you gonna convert it into to solve?

algebraic twins form

You have $\int\dfrac{x²\pm 1\ dx}{x^4+kx²+1}$, algebraic twins. What do you divide by next, then what substitutions do you take?

1. divide numerator and denominator by $x²$.

2. use substitution $x\mp \dfrac1x=t$

3. square that thang for denominator

4. differentiate that thang for numerator

How do you convert $\int\dfrac{dx}{ax^4+kx²+a}$ or $\int\dfrac{x²\ dx}{ax^4+kx²+a}$ into algebraic twins?

1. multiply and divide by 2

2. for $x²$, use $x²+1+x²-1$

3. for $1$, use $x²+1-x²+1$

4. separate

How would you integrate $\int\dfrac{x\ dx}{ax^4+kx²+a}$ ?

use substitution $x²=t \implies x\ dx=dt/2$

substitute, turn the denominator into a quadratic, solve easily

How would you integrate $\int\dfrac{x³\ dx}{ax^4+kx²+a}$ ?

use substitution $x²=t \implies x\ dx=dt/2$

substitute, turn the denominator into a quadratic, solve easily

how do you solve $\int\sqrt{\tan x}\ dx$?

use substitution $\sqrt{\tan x}=t$ then square both sides then differentiate to get

$$\sec²x\ dx=2tdt$$

then do $1+tan²x\ dx=2tdt$, resubstitute $t²$ in that then get $dx=\dfrac{2tdt}{1+t^4}$

substitute in integral

$\int\dfrac{t\cdot 2tdt}{1+t^4}$ then solve using algebraic twins

How would you solve forms like $\int\dfrac{dx}{(x-\alpha)^m(x-\beta)^n}$, where $m+n=2$?

multiply and divide the denominator by the smaller of $m$ and $n$, group, take whatever is left in fractional powers as $t$, differentiate substitution, substitute, blah

Integration By Parts formula 🗣

$$\int I\cdot II\ dx=I\int II\ dx - \int (\tfrac{dI}{dx}\int II\ dx)dx$$

What is the priority order for Integration By Parts 🗣

Also what does it mean

I → inverse functions

L → log

A → algebraic functions

T → trigonometric functions

E → exponential

It means the more easily-differentiable function should be $I$ (that is the list) (WHAT ARE WORDS)

What is $\int \ln x \ dx$?

$$\int \ln x\ dx = x\ln x-x+c$$

How would you solve $\int \sin^{-1}x\ dx$?

integration by parts 🗣

How would you solve $\int \tan^{-1}x\ dx$?

use substitution $\tan^{-1}x=t \implies x=\tan t \implies dx=\sec²t\ dt$

substitute, then solve using integration by parts

What is $\int e^x\big( f(x)+f’(x)\big) dx$?

$$e^xf(x)+c$$

If you see $\int e^x g(x)dx$ anything, what’s the first thing you do?

see if you can convert $g(x)$ into some form of $f(x)+f’(x)$.

How do you differentiate $\dfrac{(f(x))²}{2}$?

$$=f’(x)\big( f(x)\big)$$

chain rule

when you’re integrating something and there’s $1+x²$ in the denominator, what’s a safe bet to consider as $t$?

$$\tan^{-1}x=t$$

ok

check page 9 of notes

ok