STAT 164 - 3RD LE - CHAPTER 6.1

CORRELATION ANALYSIS

It is a statistical technique used to determine the strength of the relationship between two variables, X and Y.

CORRELATION ANALYSIS

it provides a measure of strength of the linear relationship between two variables measured in at least interval scale.

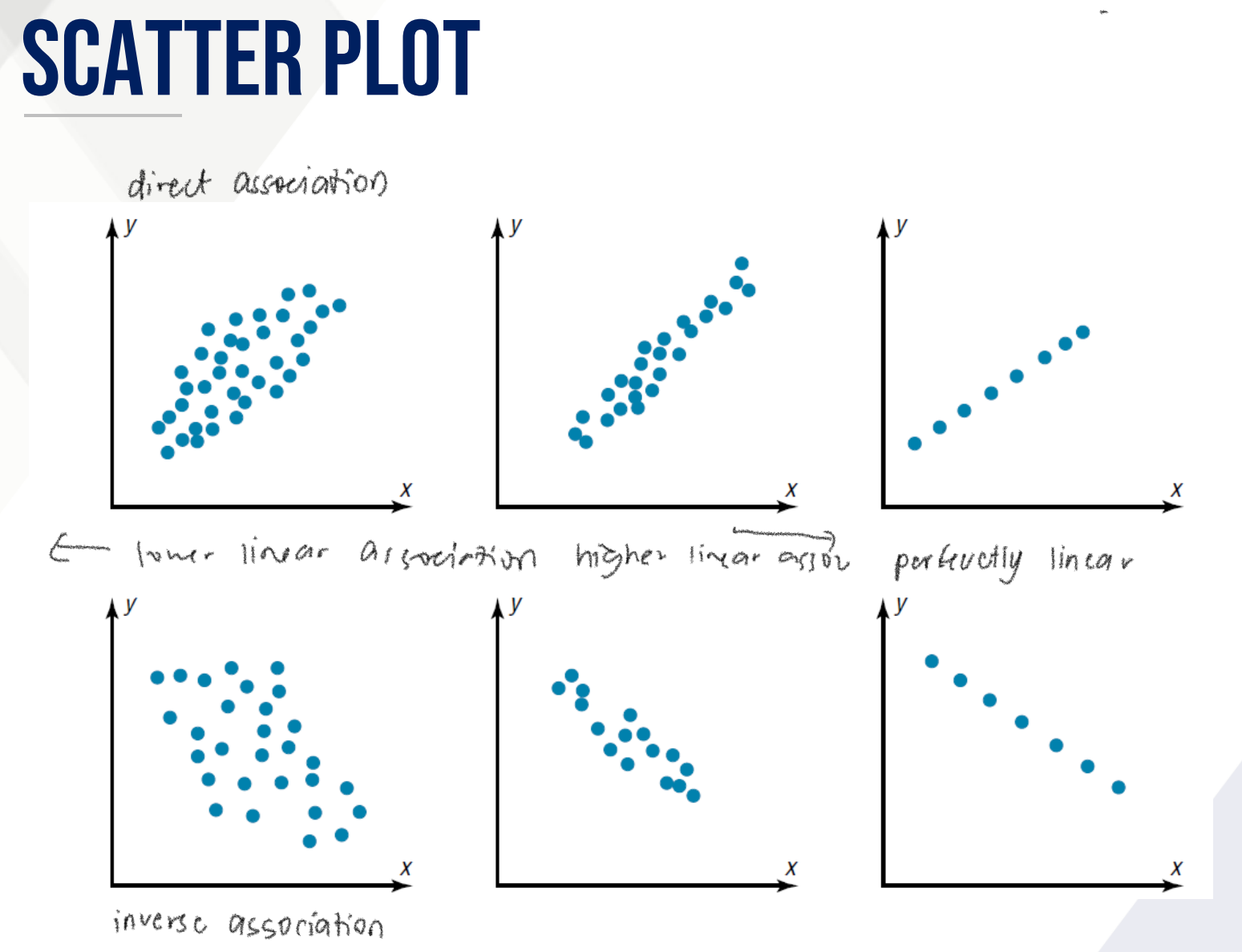
SCATTER PLOT

• a graph of the ordered pairs of numbers consisting of variables X and Y

• a visual way to describe the nature of the relationship between two quantitative variables

Correlation Coefficient

• It is a quantitative measure of the closeness or degree of relationship between two variables

• It can be computed using a particular formula depending on the characteristic of the variable of interest

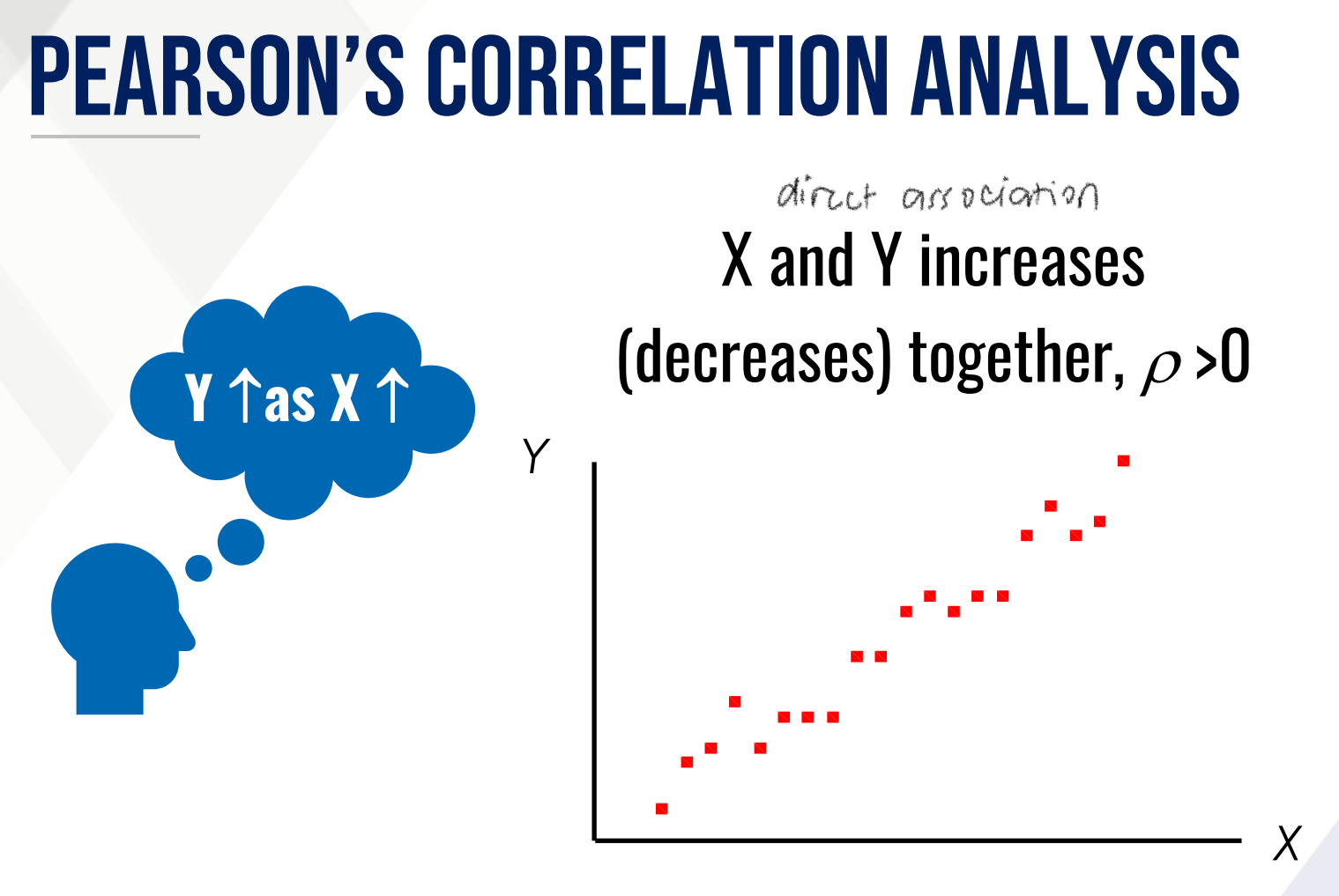
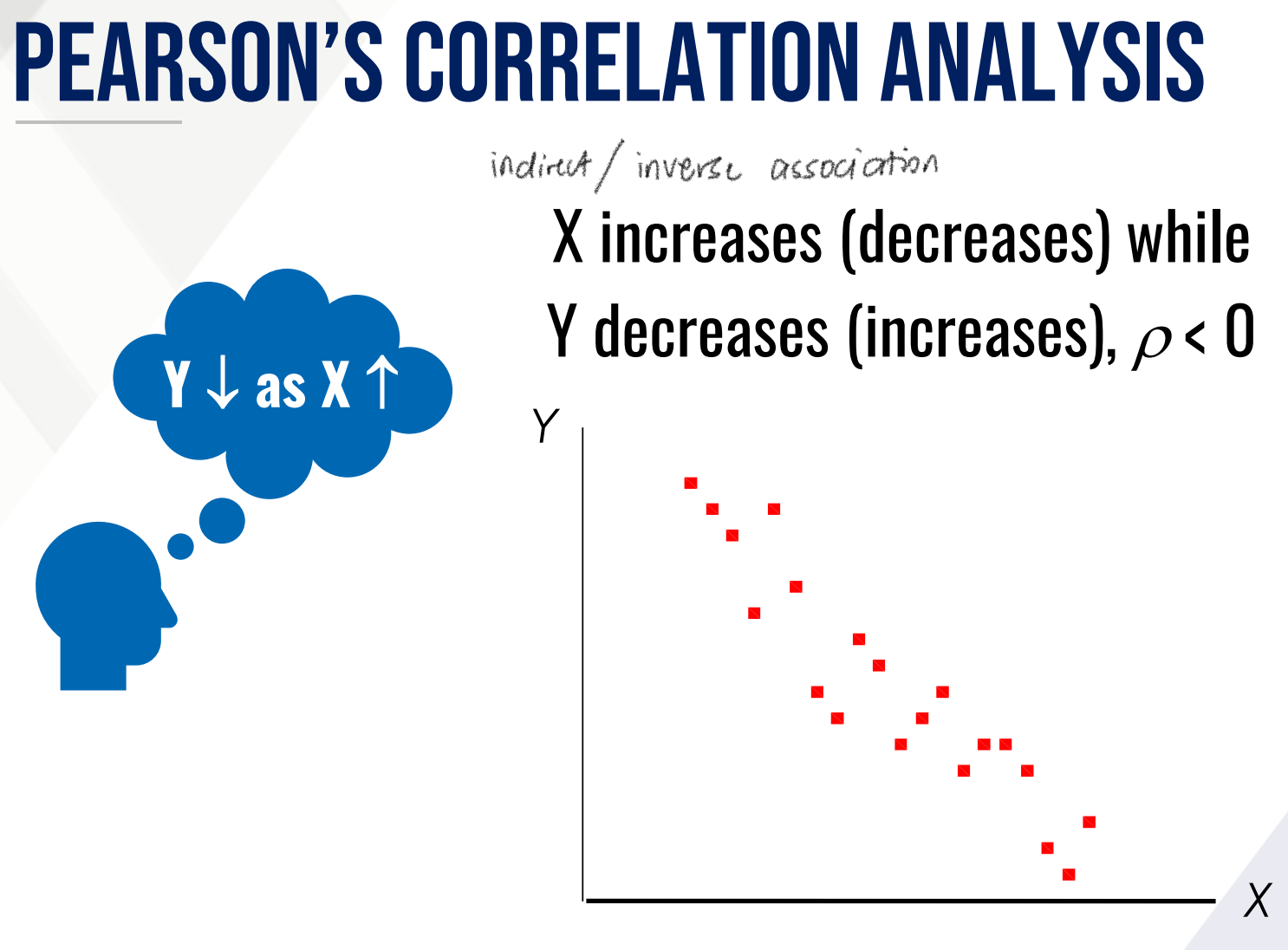
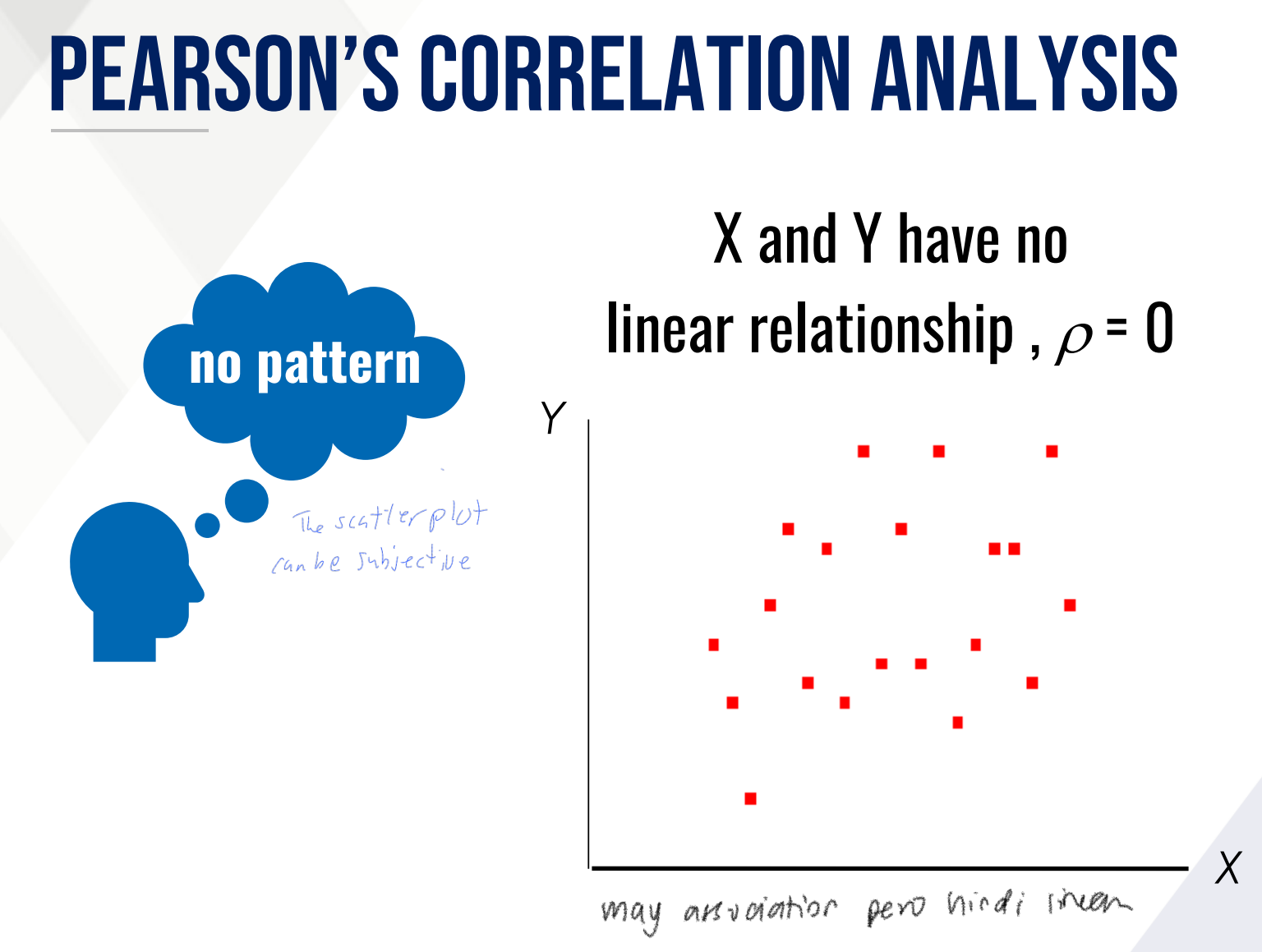
What do the following ρ ranges mean?

• ρ > 0

• ρ < 0

• ρ = 0

How about the Strength of Linear Relationship?

• Provide range and then interpretation for each.

If its ordinal we automatically cant use Pearson’s

What are the assumptions for PEARSON’S CORRELATION ANALYSIS?

1. Both variables must follow the _______________.

   • What test?

     • Ho (in words):

     • Ha (in words):

2. The variables must be measured at least in the ______________ or must be ______________.

What is the Test of Hypothesis for PEARSON’SCORRELATION ANALYSIS?

• Ho (in words):

• Ha (in words):

  • or Ha (in words): >

  • or Ha (in words): <

There is a positive (direct) strong linear association between PCV and hemoglobin level among women with anemia.

Test on Bivariate Normality, provide the following:

DH test p-value: 0.5451

• Ho (in words):

• Ha (in words):

• Decision:

• Conclusion:

Test of Hypothesis, provide the following:
p-value = 0.0011

• Ho (in words):

• Ha (in words):

• Conclusion:

SPEARMAN’S RANK ORDER CORRELATION ANALYSIS

• Uses the ranks X and Y

• measures the degree of correspondence between rankings

SPEARMAN’S RANK ORDER CORRELATION ANALYSIS

• measures how well one variable is monotonically associatd on the other variable

• variable are at least ordinal in scale

• the statistic r_s is used to estimate the true correlation, p

SPEARMAN’S RANK ORDER CORRELATION ANALYSIS

Its coefficient, ρ_s, measures the strength and direction of monotonic association between two ranked variables.

• Assumption: X and Y are at least ordinal in scale.

What is the Test of Hypothesis for SPEARMAN’S RANK ORDER CORRELATION ANALYSIS?

• Ho (in words):

• Ha (in words):

  • or Ha (in words): >

  • or Ha (in words): <

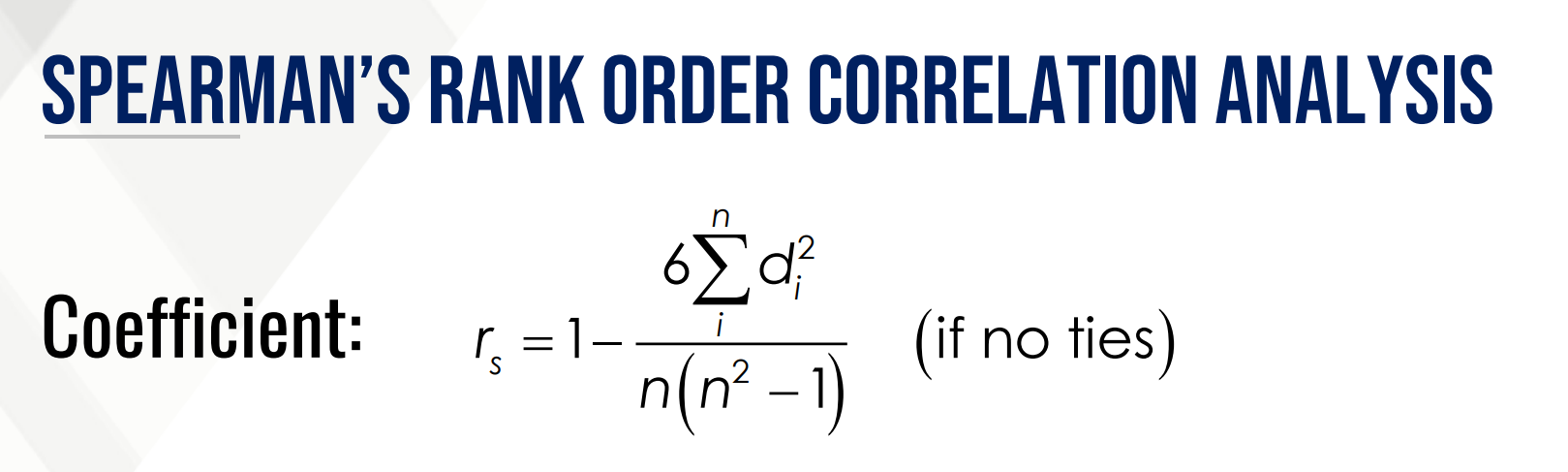
SPEARMAN’S RANK ORDER CORRELATION ANALYSIS Coefficient formula?

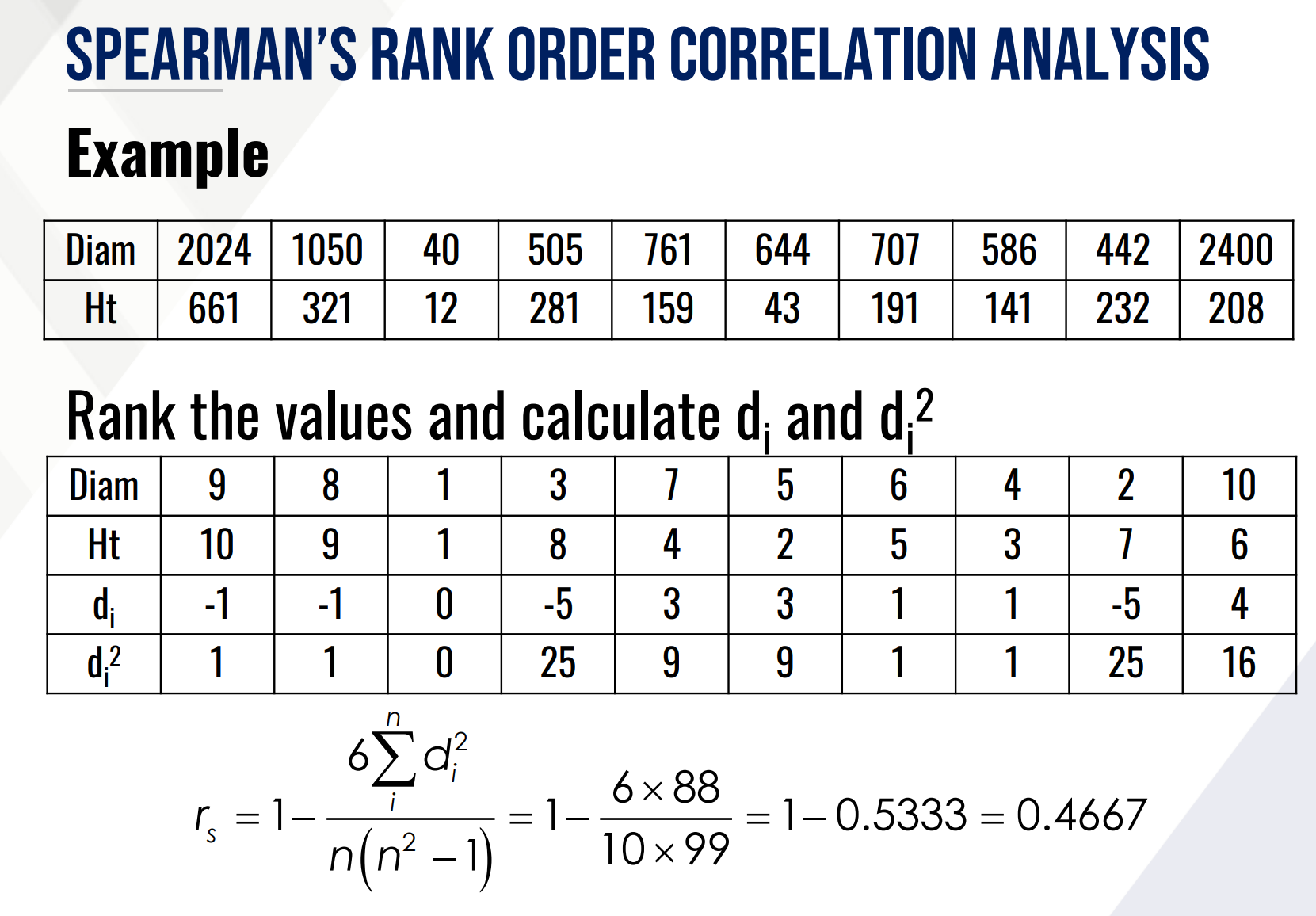
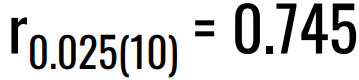
SPEARMAN’S RANK ORDER CORRELATION ANALYSIS, provide the following:

• Test statistic:

• Ho (in words):

• Ha (in words):

• Decision:

• Conclusion:

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 - Quantitative

• Variable 2 - Quantitative

• Condition - Bivariate Normality - Yes

• Measure of Association - Pearson’s Correlation Coefficient

• Corresponding Test Procedure - t-Test for Correlattion Coefficient (Pearson’s Correlation)

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 - Quantitative

• Variable 2 - Quantitative

• Condition - Bivariate Normality - Yes
  

• Measure of Association - ____________________

• Corresponding Test Procedure - ____________________

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 -

• Variable 2 -

• Condition - Bivariate Normality - No

• Measure of Association - Spearman’s Rank Order Correlation Coefficient

• Corresponding Test Procedure - Spearman’s Rank Order Correlation Analysis

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 -

• Variable 2 -

• Condition - Bivariate Normality - No
  

• Measure of Association - ____________________

• Corresponding Test Procedure - ____________________

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 - Categorical

• Variable 2 - Categorical

• Measure of Association - Phi Coefficient (2×2 continegncy table), Contingency Coefficient, Cramer’s V

• Corresponding Test Procedure - Chi-Square Test, G-Test, Fisher’s Exact Test (2×2)

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 - Categorical

• Variable 2 - Categorical
  

• Measure of Association - ____________________

• Corresponding Test Procedure - ____________________

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 - Ordinal

• Variable 2 - Quatitative

• Measure of Association - Pearson’s Correlation Coefficient

• Corresponding Test Procedure - t-Test for Correlattion Coefficient (Pearson’s Correlation)

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 - Ordinal

• Variable 2 - Quatitative
  

• Measure of Association - ____________________

• Corresponding Test Procedure - ____________________

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 - Ordinal

• Variable 2 - Ordinal

• Measure of Association - Kendall’s Rank Correlation Coefficient

• Corresponding Test Procedure - Kendall’s Rank Correlation Test

Given the variables 1 and 2, provide the measure of association and the corresponding test procedure:

• Variable 1 - Ordinal

• Variable 2 - Ordinal
  

• Measure of Association - ____________________

• Corresponding Test Procedure - ____________________

REGRESSION ANALYSIS

It is a statistical technique used to study the functional relationship between variables which allows predicting the value of one variable, say Y (dependent, outcome, or response variable), given the value of another variable, say X (independent or explanatory variable).

REGRESSION ANALYSIS

It is assumed in this technique that a change in X will lead directly to a change in Y.

LINEAR REGRESSION MODEL

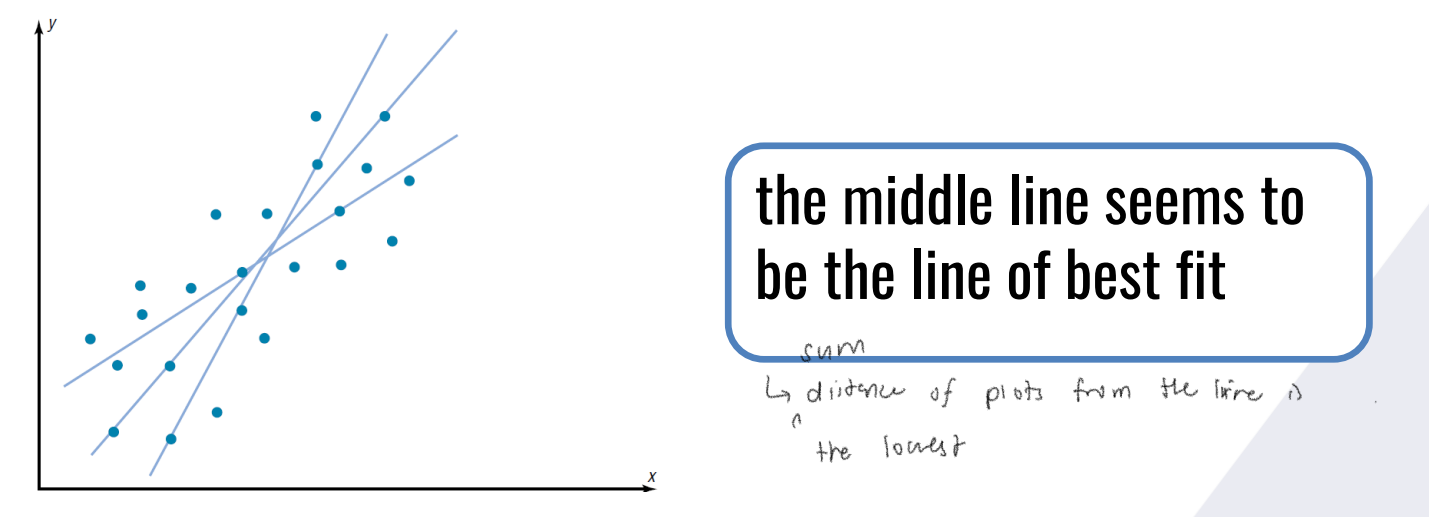
provides a linear equation representing the best fitted regression line between a quantitative Y and a set of X.

LINEAR REGRESSION MODEL

used to see the trend of association and make predictions or estimates of Y based on the data

1. error

2. independent

3. normally distributed

4. homoscedastic

LINEAR REGRESSION MODEL ASSUMPTIONS

1. The values of X are measured without ________.

2. The values of Y are statistically ______________.

3. For each value of X, there is a subpopulation of Y values that is _____________.

4. The variances of the subpopulations of Y are _____________.

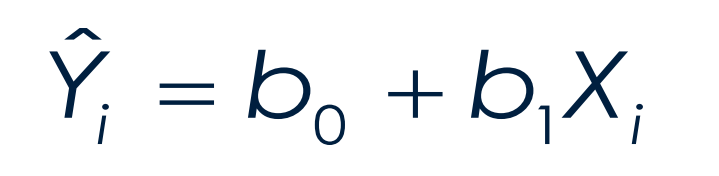
What is the formula to solve for the value of the dependent variable in a SIMPLE LINEAR REGRESSION MODEL?

• Also what is the formula for the estimated regression model?

Coefficient of Determination (R²)

• This estimates model adequacy

• proportion of the total variation in Y that is explained by X, usually expressed in %

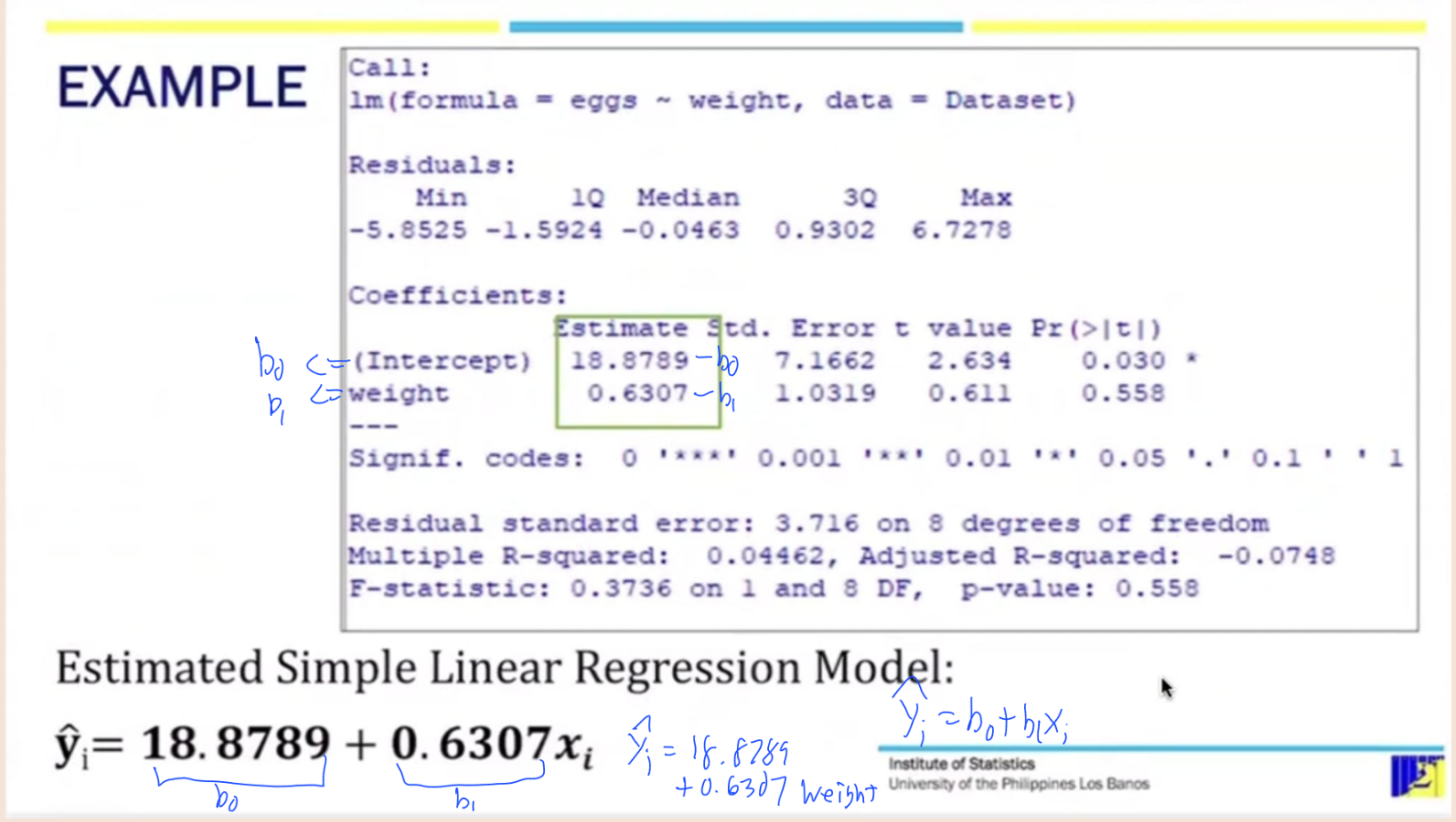
SIMPLE LINEAR REGRESSION MODEL

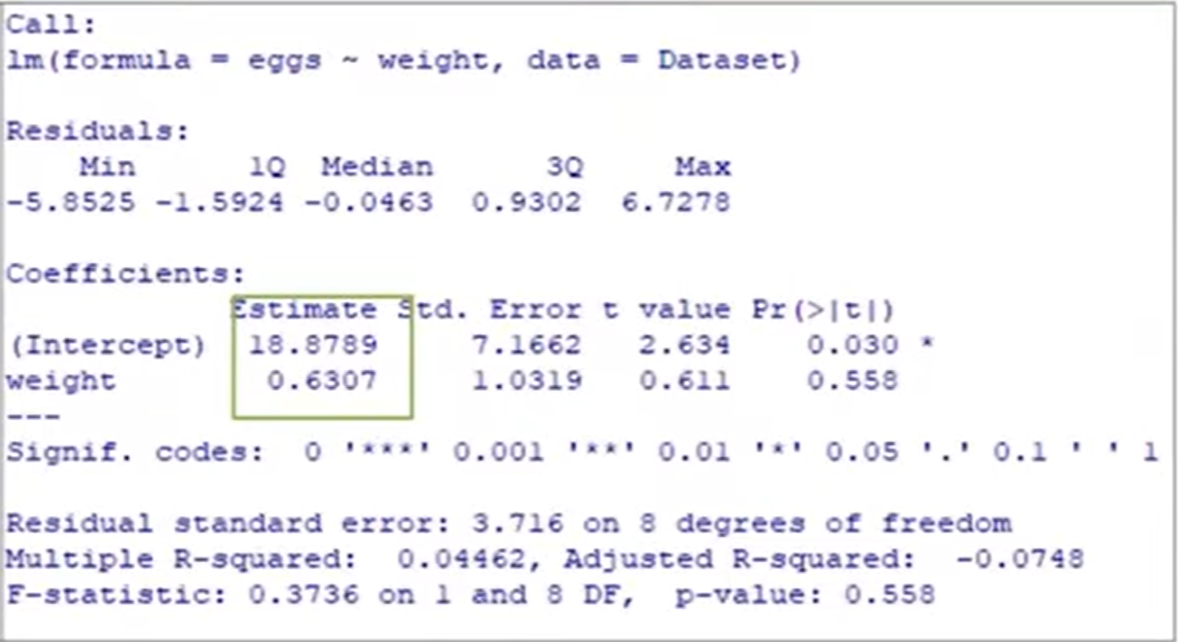
Provide the following:

• Estimated Simple Linear Regression Model:

• Interpretation of each Regression coefficient

• R²

• Interpretation of R²

What is the estimated MULTIPLE LINEAR REGRESSION MODEL formula?

Provide the following:

• Estimated Linear Regression Model

• Interpretation of the Regression Coefficients

• Interpretation of the Regression Constant

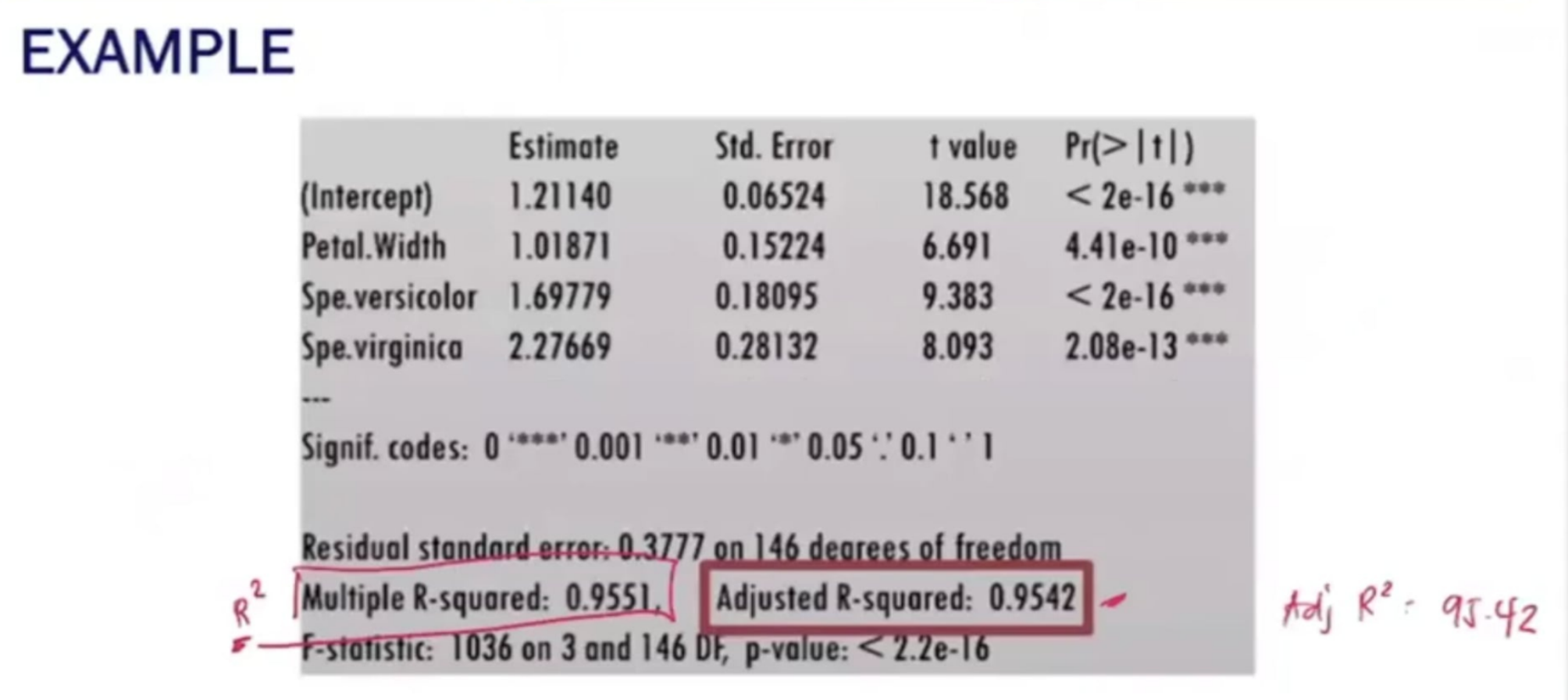
To assess the fit of the multiple linear regression model constructed, we use the Adjusted R2 instead of the R2.

MULTIPLE LINEAR REGRESSION MODEL

Provide the following:

• Ho (in words):

• Ha (in words):

• Test Procedure: F-test

• Decision Rule:

MULTIPLE LINEAR REGRESSION MODEL

What is the conclusion for each predictor? Overall?