Trigonometry formulae

Sin(a+b)

sin(a)cos(b) + cos(a)sin(b).

Sin(a-b)

sin(a)cos(b) - cos(a)sin(b)

Cos(A+B)

cos(a)cos(b) - sin(a)sin(b)

Cos(A-B)

cos(a)cos(b) + sin(a)sin(b)

Tan(A+B)

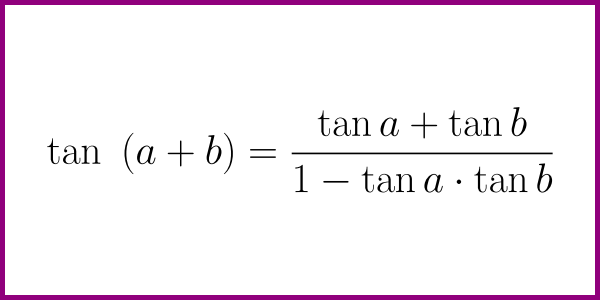
Tan(A-B)

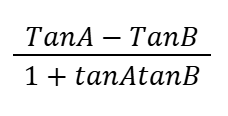
Range of sinx and cosx

-1 to 1

Range of tanx

all real numbers

180°

π radian

Sin(-x)

-sinx

Cos(-x)

Cosx

Tan(-x)

-tanx

Sin15°=Cos75°=

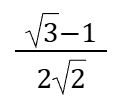
Cos15°=Sin75°=

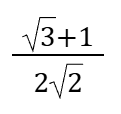
Tan15°=Cot75°=

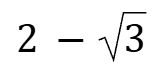
Cot 15°=Tan75°=

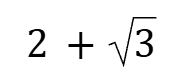
Sin18°=Cos72°=

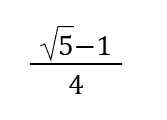
Cos54°=Sin36°=

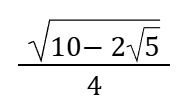
Sin54°=Cos36°=

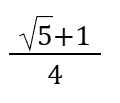
Sin72°=Cos18°=

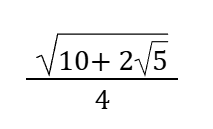
Sin22.5°=

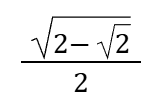
Cos22.5°

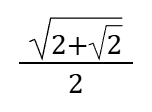
Tan22.5°

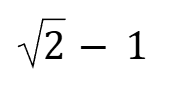
Cot22.5°

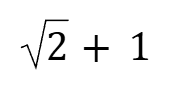
Tan(45+x)

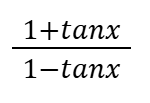
Tan(45-x)

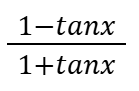
Sin(A+B) × Sin(A-B)

Sin²A - Sin²B

Cos(A+B) × Cos(A-B)

Cos²A - Sin²B

If a=b+c,

TanA × TanB × TanC = TanA - TanB - TanC

Sin2A

2SinACosA

Tan2A

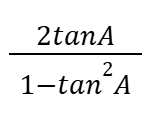
Cos2A (in terms of cos and sin)

Cos²A - Sin²A

Cos2A (in terms of sin only)

1 - 2sin²A

Cos2A (in terms of cos only)

2Cos²A - 1

1 - Cos2A

2Sin²A

1 + Cos2A

2Cos²A

1 + Sin2A

(CosA + SinA)²

1 - Sin2A

(CosA - SinA)²

SinA (in terms of 2A)

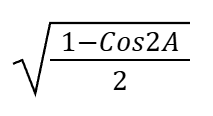
CosA (in terms of 2A)

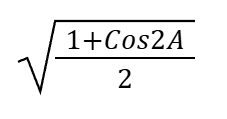
TanA (in terms of 2A)

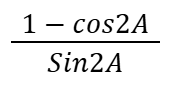
Sin2A (in terms of tanA)

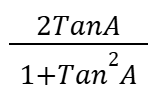
Cos2A

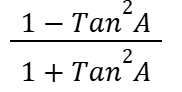
Tan²A

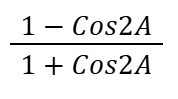
If a range of a quadratic is required, we need to find:

f(-1), f(1), f(-b/2a)

Range of SinⁿA + CosⁿA

f(0), f(45)

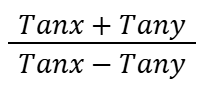
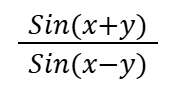
CotA - TanA

2Cot2A

Sin3A

3SinA - 4Sin³A

Cos3A

4Cos³A - 3CosA

Tan3A

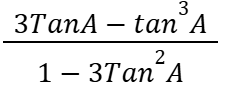
SinA Sin(60-A) Sin(60+A)

¼ Sin3A

CosA Cos(60-A) Cos(60+A)

¼ Cos3A

CosA Cos2A Cos2²A…Cos2^n-1A (n=no. of terms)

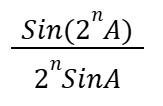
Range of asinA + bCosa

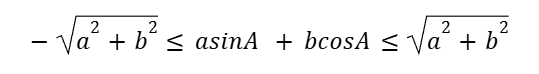
SinC+SinD

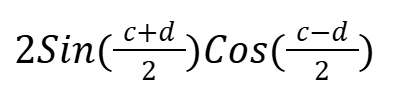
SinC - SinD

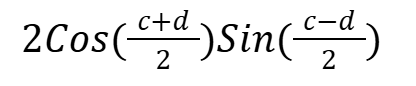
CosC + CosD

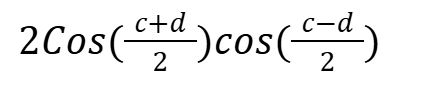
CosC - CosD

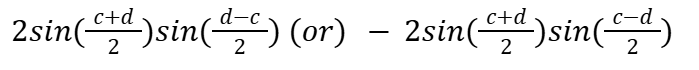
2SinACosB

Sin(A+B) + Sin(A-B)

2CosASinB

Sin(A+B) - Sin(A-B)

2CosACosB

Cos(A+B) + Cos(A-B)

2SinASinB

Cos(A-B) - Cos(A+B)

sina + sin(a+d) + sin(a+2d) +…+ sin(a+(n-1)D)

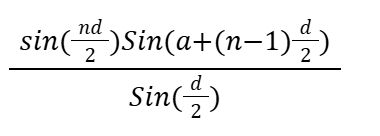
cosa + cos(a+d) + cos(a+2d) +…+ cos(a+(n-1)d)

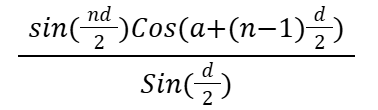
if sinx = sinα

x=nπ + (-1)ⁿα (α = (-π/2, π/2))

If cosx = cosα

x= 2nπ +- α (α = (0, π))

tanx = tanα

x= nπ + α (α = (-π/2, π/2))

sin²x = sin²α, cos²x = cos²α, tan²x = tan²α

x = nπ +- α