Chi-squared Analysis

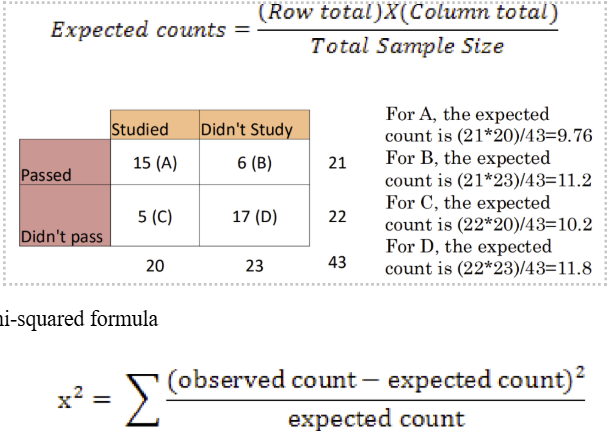
What is contingency table

Examines the question of whether 2 categories of classification are independent of each other 

• If they are independent, what frequency would we expect in each of the cells 

What is a chi-squared test

evaluates relationships between two nominal or ordinal variables (similar to a correlation analysis) 

• Compares tallies/counts of categorical responses between 2 (or more) independent groups 

• Can only be used on actual numbers and NOT %%, proportions, or means 

• Significant results tells you the data is “contingent” on the category in the margin 

• Looks at how different the observed frequencies are from the expected frequencies (p-value) 

What is a Fisher exact test

Alternative Chi-square test to use when there are few counts 

• If the frequencies/counts are less than 5 

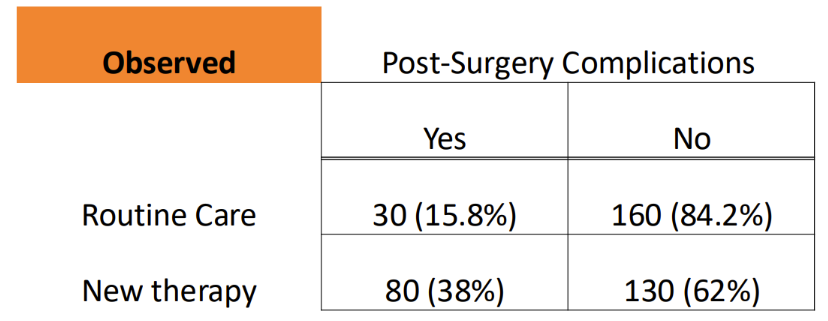
How do you calculate the expected frequencies of a contingency table

If the null is true (expected) = 

• You add the total of the column, and divide it by the total collected sample => to get the expected frequencies 

110/400 = 27.5%

(160+130)/400 = 72.5%

If the null is true, we expect 27.5% (110/400 patients – 400 patients total from both groups) of the routine and new therapy group patients.  

• 190*(0.275) = 52 patients with complications from routine care

  • 190 = 30+160 (row of routine care)

• 210*(0.275) = 58 patients with complications from new therapy

  • 210 = 80+30 (row of new therapy)

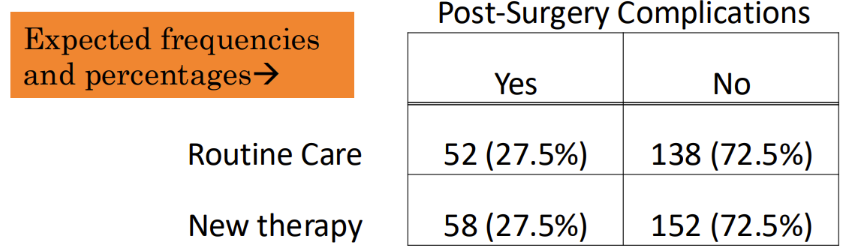
How does Chi-squared compare the observed frequencies to the expected frequencies

Compare Chi-squared statistic to a critical value to determine the p-value (will NOT be given a p-value when calculating it by hand – only a critical value) 

• Significant p-value = difference is NOT due to chance 

X^2 > critical value => SIGNIFICANT DIFFERENCE  

• P < 0.05 

therefore 

Reject the null  

* doesn’t tell you HOW strong the relationship is, only that there is one 

X^2 < critical value => no significant difference 

• P > 0.05  

Therefore 

Fail to reject the null 

How is Chi-squared interpreted for statistical significance

Null = there is no relationship between variable A (studying) and variable B (passing) 

Alternative = there is a relationship between variable A and variable B 

CORRELATION DOES NOT imply causation 

X^2 > critical value => SIGNIFICANT DIFFERENCE  

• P < 0.05 

therefore 

Reject the null  

* doesn’t tell you HOW strong the relationship is, only that there is one 

X^2 < critical value => no significant difference 

• P > 0.05  

Therefore 

Fail to reject the null 

How do you calculate Chi-squared by hand?

Steps:

1. Calculate expected counts (the frequency/number of subjects in given category if there was NO relationship between variables) 

2. Use the Chi-squared formula 

   • For each cell (A-D), calculate the difference between expected and observed 

   • Square it  

   • Divide by expected count for the given cell (A-D) 

3. Add all the values (A-D) together and get the Chi-square statistic 

4. Compare Chi-squared to the critical value