Scholarship Probability Concepts and Distributions

Scholarship Statistics Study!

poisson distribution fits data if…

• events occur ________

• occurence of each event is ________

• probability of observing a single event over a small interval is ________ to the size of the interval

• events cannot occur ________

acronym is ________

randomly, independent, proportional, simultaneously, RIPS’

the number of calls at a help desk fits a ________ distribution

poisson

for poisson distribution, lambda, λ, is the ________ number of occurrences of the event over a time ________, or the ________

mean, interval, rate

we can assume ________ when making calculations using a poisson distribution

independence

for ________ poisson, we must calculate P(X = __) to work back to find the ________, λ

P(X = 0) = e^(^-λ) so λ = -ln P(X = 0)

inverse, 0, rate

binomial distribution fits data if…

• there is n number of ________ trials

• there are __ possible outcomes: s________ and f________

independent, 2, success, failure

for binomial distribution, probability of success is given by __

p

for binomial distribution, probability of failure is given by __

q

does binomial distribution require replacement, or no replacement?

replacement

the number of possible ________ is found using the nCr button

OPTN —> PROB —> nCr

combinations

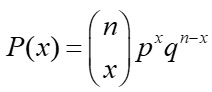
this formula is used for ________ distribution, where:

• n is the total ________ of ________

• x (or r) is the ________ of ________ outcomes

• p is the ________ of ________

• q is the ________ of ________

binomial, number, trials, number, successful, probability, success, probability, failure

for binomial distribution, p + q = __

1

the number of combinations for 1 success or 1 failure is __, while the number of combinations for all outcomes being successes/failures __

n, 1

rectangular distribution is used for c________, r________ variables which are ________ ________

continuous, random, equally likely

total area of a graph for rectangular or triangular distribution = __

1

the probability at a specific value for rectangular and triangular distributions is __ as the variable must be ________

0, continuous

a triangular distribution is used for c________, r________ variables with a ________ distribution

continuous, random, skewed

for a triangular distribution, the ________, __, is the most likely outcome

mode, c

to work out ________ of a triangular distribution, using A = ½xy, must first work out the ________, or y value, which is calculated using ________ equations for a ≤ x ≤ c and c ≤ x ≤ b

area, height, separate

for ________ distribution, h = 1 ÷ (b – a)

rectangular

for ________ distribution, h = 2 ÷ (b – a)

triangular

the ________ ________, or E(X), is the ________ value, which has the symbol x̄ or μ

expected value, mean

to find E(X) from a probability table, you must…

1. take the 1st __ value

2. multiply x by its ________

3. ________ for each x value

4. ________ all to find E(X)

x, probability, repeat, add

variance and standard deviation are a measure of the ________ of the data

spread

________ = √________

standard deviation, variance

to calculate standard deviation, you must first calculate ________

variance

to calculate variance of a ________ from a probability table (using the condensed version), you must…

1. ________ the first x value

2. ________ x by its ________

3. ________ for each x value

4. ________ all to find E(X²)

5. calculate and square the ________ (E(X) or μ) to find (E(X))² or μ²

6. calculate E(X²) – μ² = ________

population, square, multiply, probability, repeat, add, mean, variance

Var(X) = ________

variance

SD(X) = ________

standard deviation

σ is the symbol for ________ of a ________

standard deviation, population

s is the symbol for ________ of a ________

standard deviation, sample

σ² is the symbol for ________ of a ________

variance, population

s² is the symbol for ________ of a ________

variance, sample

to calculate variance from a recorded set of values…

1. find the ________ of each x value from the mean, μ

2. ________ each of these values

3. ________ all

4. divide the sum by…

   i. the total number of values, n, for the ________ (σ²)

   ii. n – 1, for the ________ (s²)

difference, square, add, population, sample

if finding the mean of x multiplied by a constant, a, E(aX) = __ x E(X)

a

if finding the standard deviation of x multiplied by a constant, a, SD(aX) = __ x SD(X)

|a|

if finding the variance of x multiplied by a constant, a, Var(aX) = __ x Var(X)

a²

if finding the mean of the sum of x and a constant, b, E(X+b) = E(X) + __

b

if finding the standard deviation of the sum of two random variables, x and y, you must first find the ________, then take the ________

variance, square root

if finding the standard deviation of the sum of x and a random variable, b, SD(X+b) = ________

SD(X)

if finding the variance of the sum of x and a random variable, b, Var(X+b) = ________

Var(X)

SD(X) and Var(X) do not change when ________ a random variable to/with x

adding

if finding the expected value to the sum of two random variables, X and Y, E(X±Y) = E(X) __ E(Y)

±

if finding the variance of the sum of two random variables, X and Y, Var(X±Y) = Var(X) __ Var(Y)

+

when calculating the expected value and variance of the difference of two random variables, X - Y, are the individual expected values or variances for each of X and Y added (rather than subtracted)?

variances

when finding values for the sum of two random variables, X and Y, they must be ________

independent

if a value from an expectation algebra calculation does not match up with given statistics for a distribution, then the variables X and Y must be ________ probabilities, rather than ________

conditional, independent

when graphing, the ________ is the central point of the dataset

mean

a normal distribution has a ________ curve

bell-shaped

for normal distribution, either side of the mean should fall within __ x SD(X)

3

if finding values either side of the middle 95% of data for a normal distribution, the ________ function must be used, setting the area to ____

InvN, 0.95

should ncd or npd be used when finding the probability over an interval?

ncd

should ncd or npd be used when finding the height of a probability function at a specific value for X?

npd