MO 8. Przybliżenia różnicowe dla f'(x), błędy obcięcia przybliżeń T.

Problem wyznaczenia przybliżenia różnicowego pochodnych funkcji

Postawienie problemu :

Jak obliczyć przybliżone wartości pochodnych funkcji y = f(x), mając jedynie zadane wartości funkcji w punktach x₀, x₁... x_n ?

Jest to trudny problem, bo nie mamy informacji o zachowaniu funkcji pomiędzy punktami x_i.

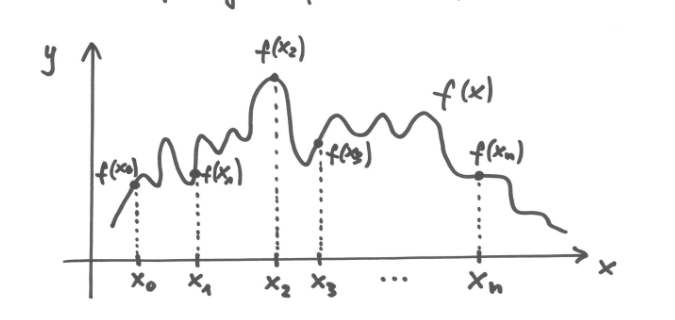
Punkty x₀, x₁... x_n

Węzły siatki dyskretnej.

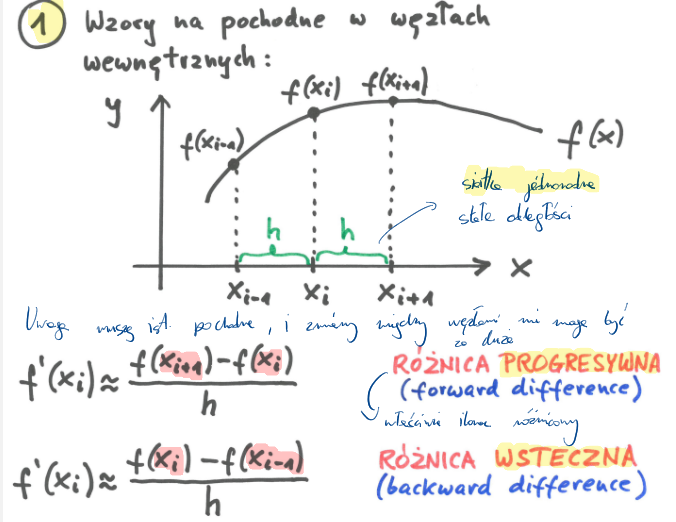
Wzory na przybliżenia pochodnych dwupunktowych w węzłach wewnętrznych.

Różnica wsteczna,
Różnica progresywna.

Uwaga muszą ist. przybliżane wart. pochodnych - zmiany między węzłami nie mogą być za duże.

Przybliżenia pochodnych trzypunktowych

Różnica centralna

Przybliżenia pochodnych trzypunktowych dla 2 pochodnej

Różnica centralna dla 2 pochodnej

Rozwinięcie funkcji w szereg Taylora i analiza błędu obcięcia (dyskretyzacji)

Uwaga:

• zakładamy istnienie n-tej pochodnej

• rozwijamy funkcję wokół punktu x_i a liczymy dla np. x_i+1 lub x_i-1

• O(h) - błąd obcięcia - pewna niewielka wartość proporcjonalna do h

Błąd obcięcia dla różnic centralnych

Ogólny wzór obcięcia dla przybliżeń różnicowych

p - rząd dokładności przybliżenia

A - współczynnik wyrazu dominującego

A, B, C,.. - współczynniki zależne od wyższych pochodnych f(x)

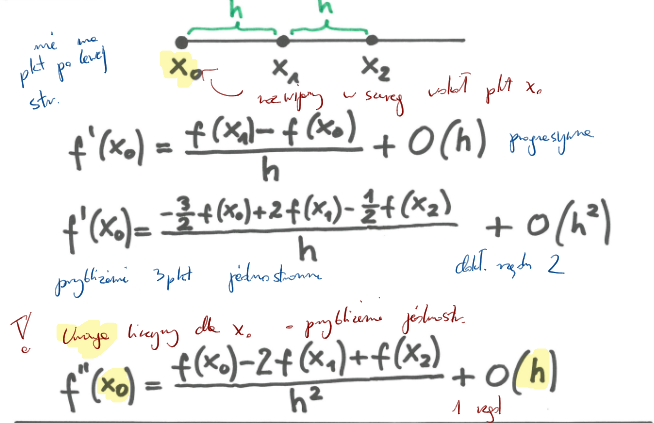
Wzory dwu - trzypunktowe dla pochodnych w węzłach końcowych siatki (prawostronne)

Rozwinięcie wokół x₀

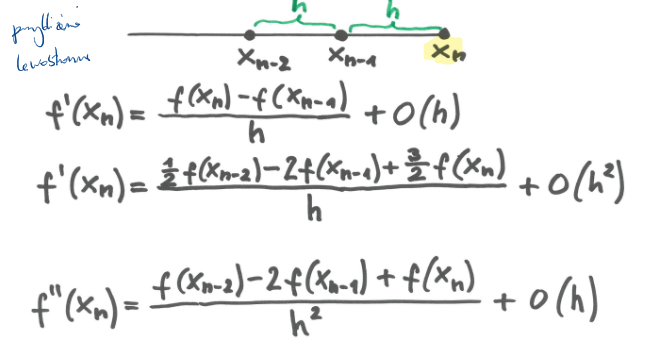
Wzory dwu - trzypunktowe dla pochodnych w węzłach końcowych siatki (lewostronne)

Analiza błędów z uwzględnieniem wpływu błędów maszynowych

e - błąd reprezentacji liczbowej

δ_O - błąd arytmetyczny odejmowania

δ_D - błąd arytmetyczny dzielenia

• pomijamy błąd reprezentacji h

• pomijamy błędy działań arytmetycznych δ

• liczymy bewzgl. wart. z błędu przybliżenia |f’_przyb(x_i) - f_przyb(x_i)|

• wyznaczamy błąd maszynowy i obcięcia

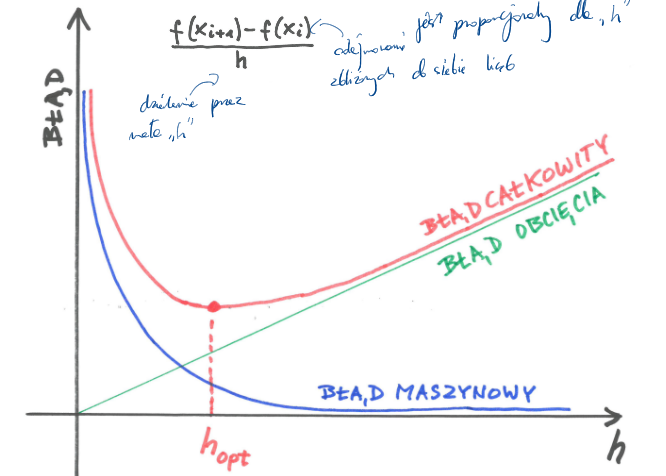
• Błąd maszynowy jest odwrotnie proporcjonalny do h

• A błąd obcięcia jest wprost proporcjonalny do h

Zależności między błędami

Teoretycznie najlepszym wyborem jest h_opt - odpowiada najmniejszemu błędowi całkowitemu.

Natomiast w praktyce należy wybierać h » h_opt, bo mamy większą kontrolę nad błędem obcięcia.

Wyprowadzanie wzorów na pochodne

w ogólnym przypadku siatek niejednorodnych

Dwie alternatywne metody:

1) Rozwinięcia w szereg + warunki zgodności 2 pochodną + minimalizacja błędu obcięcia.
2) Różniczkowanie analityczne wzorów interpolacyjnych Lagrange’a

Metoda wyprowadzenia wzoru trzypunktowego na pierwszą pochodną w wewnętrznym węźle siatki niejednorodnej

1. Rozwinięcie f(x_i+1) i f(x_i-1) wokół x_i

2. Mnożymy współczynniki do wyznaczenia (a,b,c) przez rozwinięcia funkcji. Otrzymujemy pochodną + T (błąd obcięcia)

3. Grupujemy wyrazy zgodnie z kolejnymi pochodnymi

4. Minimalizujemy T rozwiązując układ równiań

5. Gotowy wzór na f’(x_i)