Teoria

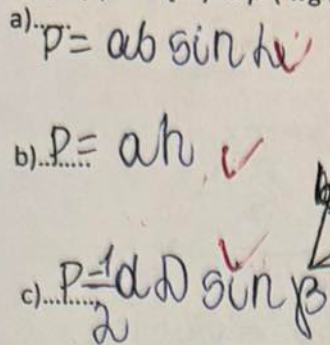
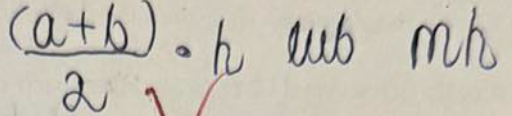
Przekątne w rombie mają następujące własności:

Przekątne w prostokącie mają następujące własności:

Przekątne w równoległoboku mają następujące własności:

Przekątne w kwadracie mają następujące własności:

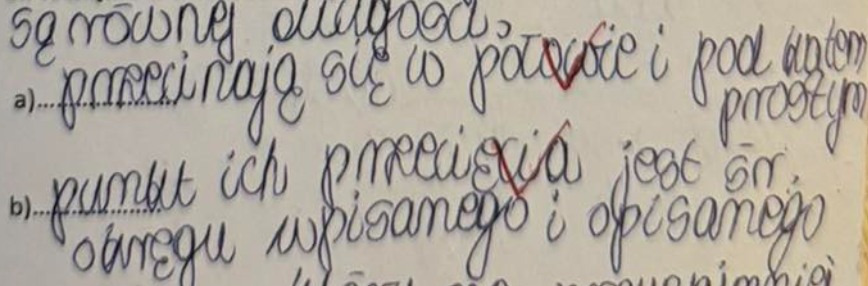
Trapez to czworokąt

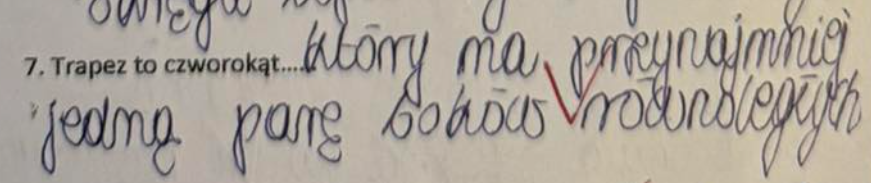
Trapezoid to czworokąt, który

nie ma żadnych boków równoległych

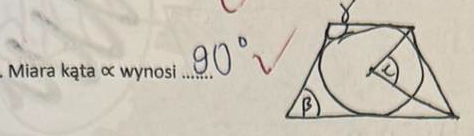
Twierdzenie Ptolemeusza

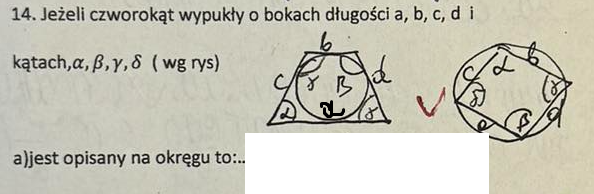
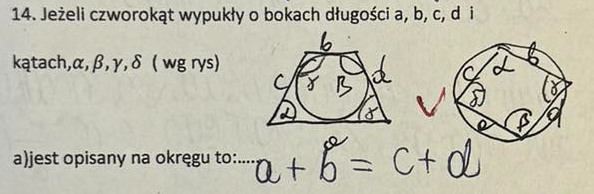
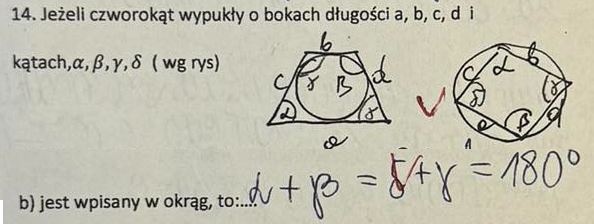
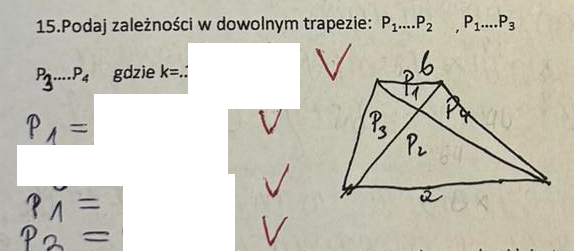
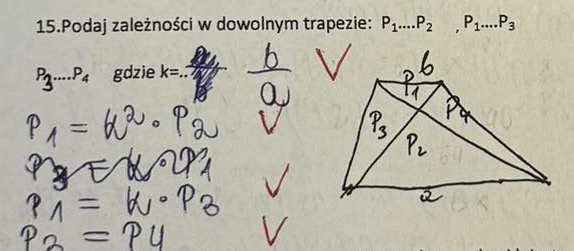
Deltoid to czworokąt, którego:

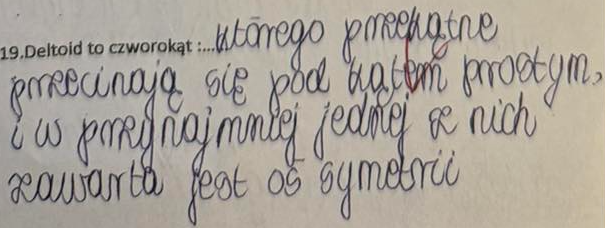
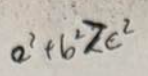
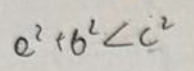
Kąt wewnętrzny n-kąta foremnego wynosi:

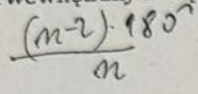
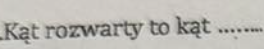
Okręgi o (S₁,r₁) i o(S₂,r₂) są rozłączne zewnętrznie. gdy

|S₁S₂| > r₁+r₂

Okręgi o (S₁,r₁) i o(S₂,r₂) są styczne zewnętrznie, gdy

|S₁S₂| = r₁+r₂

Okręgi o (S₁,r₁) i o(S₂,r₂) mają 2 punkty wspólne, jeżeli

|r₁-r₂| < |S₁S₂| < r₁+r₂

Okręgi o (S₁,r₁) i o(S₂,r₂) są styczne wewnętrznie

|r₁-r₂| = |S₁S₂|

Okręgi o (S₁,r₁) i o(S₂,r₂) są rozłączne wewnętrznie, gdy

|r₁-r₂| > |S₁S₂|

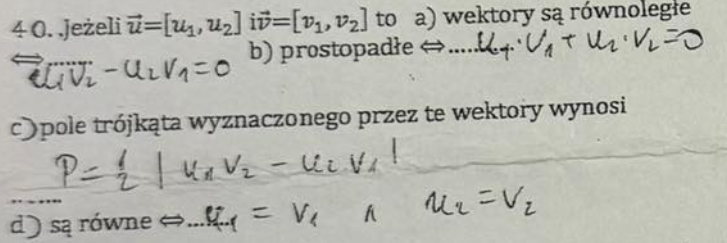
Z trzech odcinków o długościach a, b, c można zbudować trójkąt ⇔

(a+b>c) i (b+c>a) i (a+c>b)

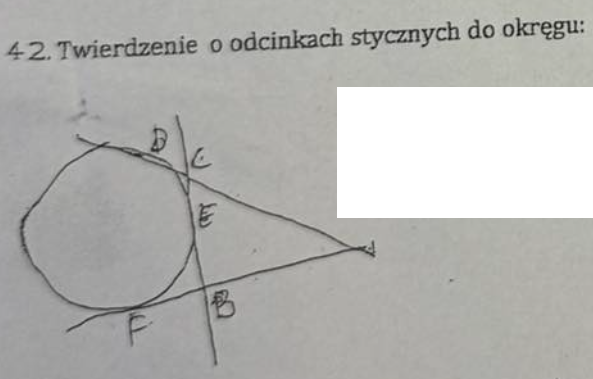
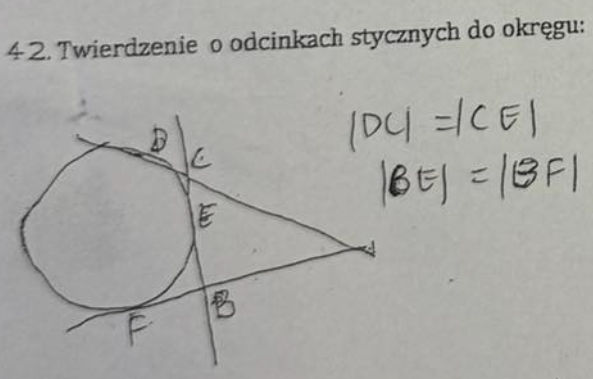
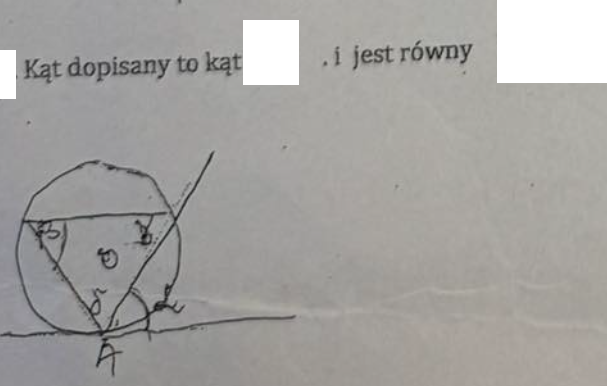
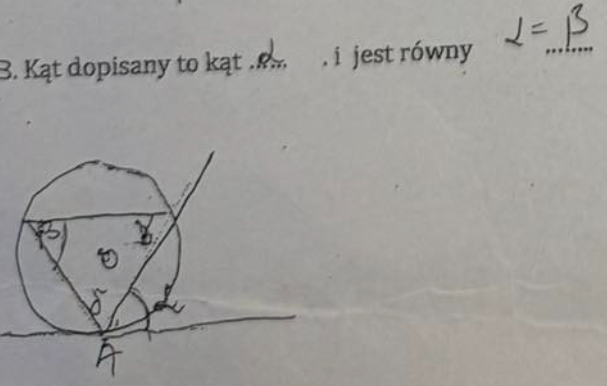
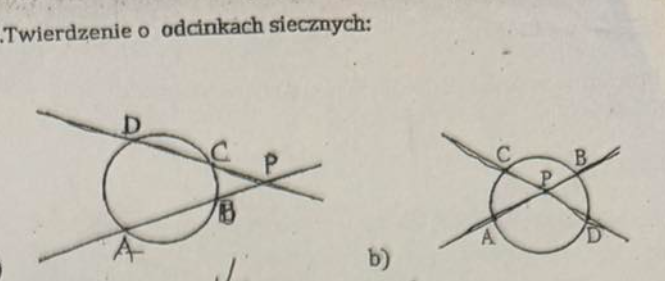
|PA| × |PB| = |PC| × |PD|

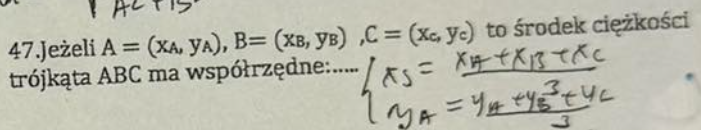
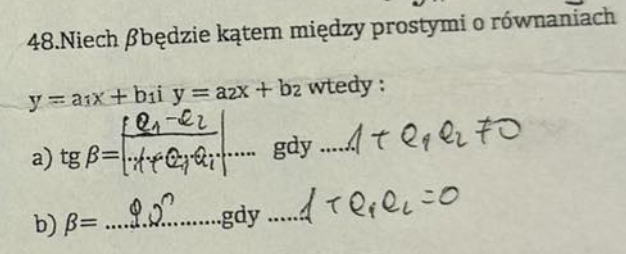
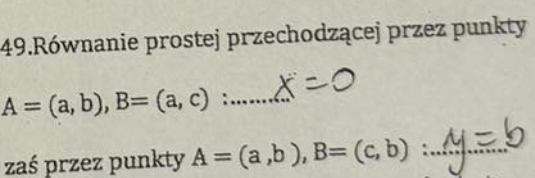
Trapez to czworokąt, który ma:

co najmniej jedną parę boków równoległych

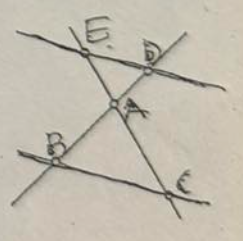
Twierdzenie Talesa

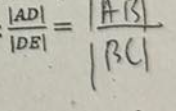
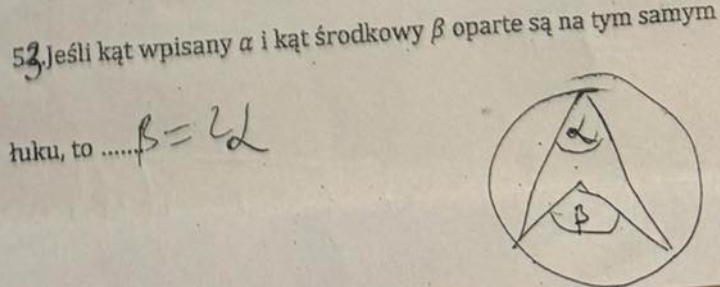
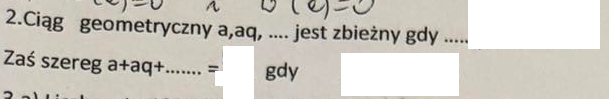
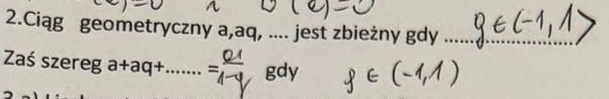
Liczba y to 120% liczby x. Czyli y=

1,2x

O ile % liczba 8 jest większa od liczby 5

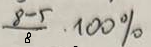
O ile % liczba 5 jest mniejsza od liczby 8

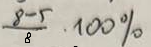
Liczba y jest o 20% mniejsza od liczby x. Czyli x=

0,8x

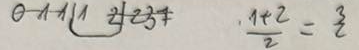
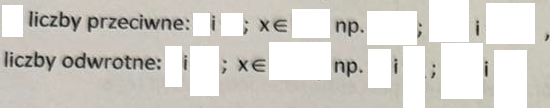
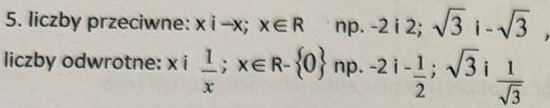
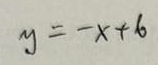
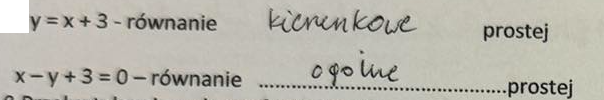
Przekształć wykres funkcji y=f(x) względem symetrii względem osi OX

y=-f(x)

Przekształć wykres funkcji y=f(x) względem symetrii względem punktu O

y=-f(-x)

Przekształć wykres funkcji y=f(x) względem symetrii względem osi OY

y=f(-x)

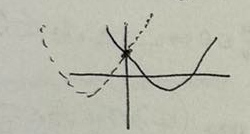
Przekształć wykres funkcji y=f(x) tak, że |f(x)|

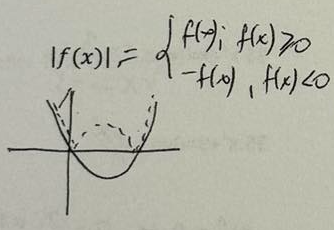
Przekształć wykres funkcji y=f(x) tak, że f(|x|)

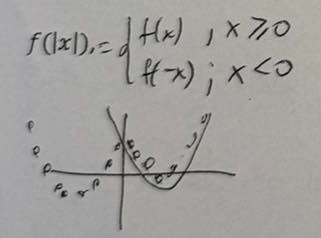
Przekształć wykres funkcji y=f(x) tak, że 2f(x)

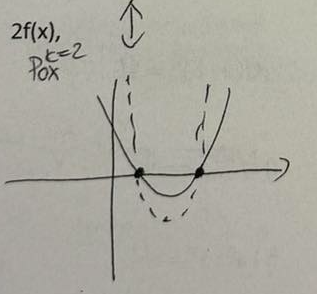
Przekształć wykres funkcji y=f(x) tak, że f(2x)

Pole boczne stożka (2 wzory)

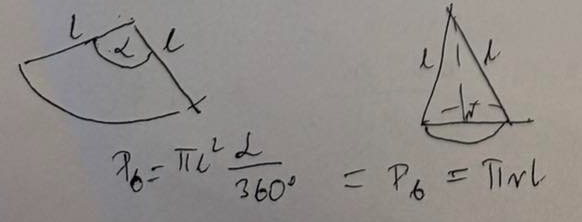
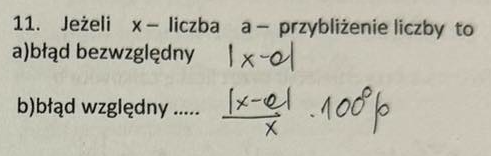
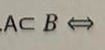
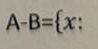
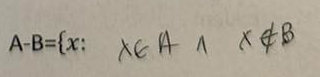
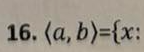
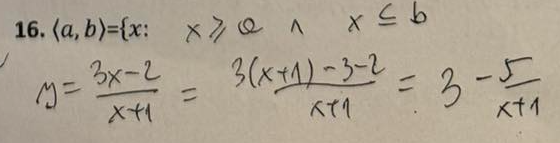
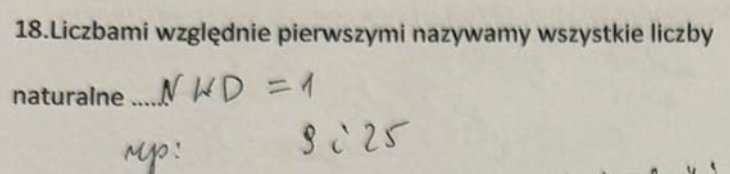
Liczby pierwsze to liczby naturalne, które

a×b≠0 ⇔

a≠0 i b≠0

Liczby złożone to liczby naturalne, które

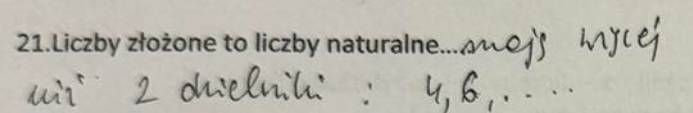
Liczba całkowita a przy dzieleniu przez liczbę całkowitą b daje resztę r ⇔

Liczba całkowita a przy dzieleniu przez liczbę całkowitą 3 daje resztę 1 to ma postać …… lub ……

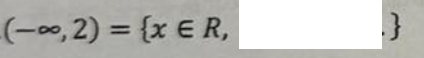
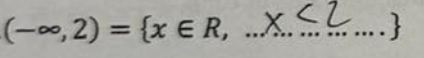
a×b>0 ⇔

(a>0 i b>0) lub (a<0 i b<0)

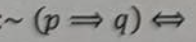
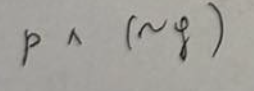
Liczba wymierna to liczba, którą……………………… i jej rozwinięcie dziesiętne jest ułamkiem………………………….

Liczba jest podzielna przez 4, jeżeli

2 ostatnie cyfry tworzą liczbę podzielną przez 4

Liczba jest podzielna przez 6, jeżeli

jest podzielna zarówno przez 2 i przez 3

Liczba jest podzielna przez 9, jeżeli

suma cyfr tej liczby jest podzielna przez 9

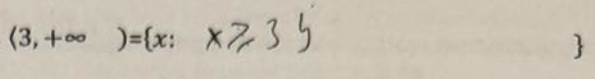
a×b=0 ⇔

a=0 lub b=0

a×b<0 ⇔

(a>0 i b<0) lub (a<0 i b>0)

|a|=

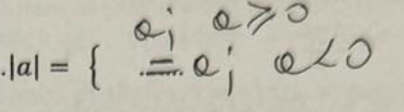
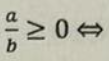
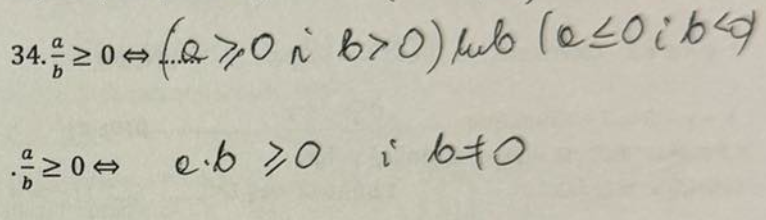
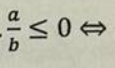
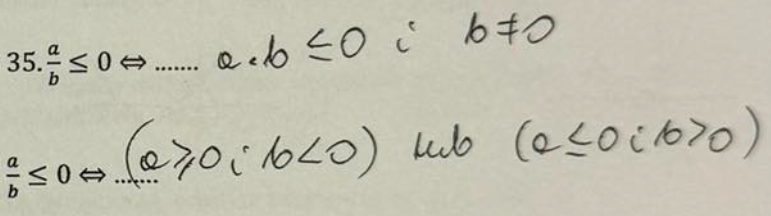
x²-9=0⇔

x=3 lub x=-3

x²-9x=0⇔

x=0 lub x=9

x²+9=0⇔

∅

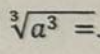
a

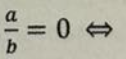
a=0 i b≠0

(aⁿ)^m=

a^nxm

(a×b)ⁿ=

aⁿ×bⁿ

a⁰=

a=1 dla a≠0

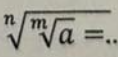
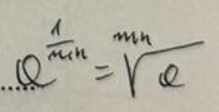
a^-1=

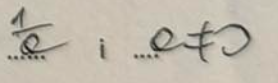
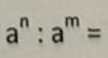
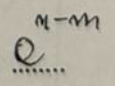
|a|+|b|=0⇔

a=0 i b=0