Further Maths Pure Core Formulae

3x3 matrix for a rotation of θ degrees anticlockwise about the y axis

Rotation of θ degrees anticlockwise about the x axis

Rotation of θ degrees anticlockwise about the z axis

α + β

-b / a

αβ

c / a

α + β + γ

-b / a

αβγ

-d / a

αβ + γβ + αγ

c / a

Σα

α + β + γ

Σαβ

αβ + γβ + αγ

3x3 matrix of a reflection in x = 0 (the y-z plane)

3x3 matrix of a reflection in y = 0 (the x-z plane)

3x3 matrix of a reflection in z = 0 (the x-y plane)

α + β + γ + σ

-b / a

αβγσ

e / a

αβ + αγ + ασ +βγ + βσ + γσ

c / a

αβγ + αβσ + αγσ + βασ

-d / a

The formula for the perpendicular distance from the point (α,β,γ) to a plane

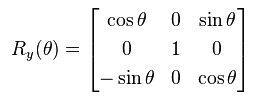
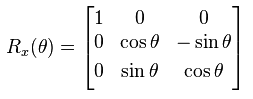
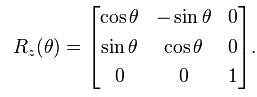
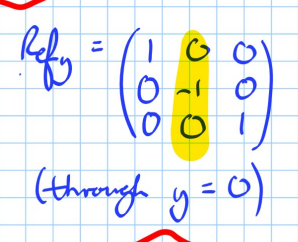
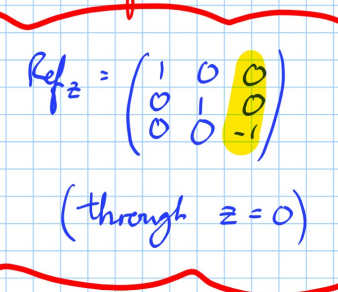
if f(x) = c, what would the substitution for the particular integral be?

a

if f(x) = bx+c, what would the substitution for the particular integral be?

ax + b

if f(x) = ax² + bx +c , what would the substitution for the particular integral be?

ax² + bc + c

if f(x) = Pe^(px), what would the substitution for the particular integral be?

Qe^(px)

OR Qxe^(px)

OR Qx²e^(px)

if f(x) = rcos(wx) + s sin(wx), what would the substitution for the particular integral be?

pcos(wx) + qsin(wx)

If an object is moving with simple harmonic motion…

the only force on it is proportional to the displacement, but in the opposite direction

i.e. F=-kx

the force increases as you get further from the starting position

So F=ma…

-kx = m a = mx:

which means x: = -k/m (x)

WHICH IS OFTEN WRITTEN AS x: = -w²x

When is simple harmonic motion simple?

when it assumes there’s no resistive force (e.g. friction)

What is damping?

the act of stopping the oscillations

then more realistic

resistance can be modelled as being proportional to the velocity, acting in the direction opposite to motion

i.e. -r dx/dt

THUS HAS THE 3 TYPES OF DAMPING (underdamped, critically damped and overdamped)

m² + rm + x = 0

What’s the difference between free vibrations and forced vibrations?

Free - they’re set in motion and then just left to it

m² + rm + x = 0

Forced - if you add an external force

m² + rm + x = f(t)

What is the general solution to x: = -w²x ?

x = Acoswt + Bsinwt