Linear Algebra Def.

The Pivot of a row in a matrix is…

The leftmost nonzero entry in that row.

A matrix is in row echelon form if…

(1) all rows consisting only of zero are at the bottom

(2) the pivot of each nonzero row is in the column to the right of the pivot in the row above it

A matrix is in reduced row echelon form if

(1) the matrix is in echelon form

(2) the pivot in each nonzero row is 1

(3) each pivot is the only nonzero entry in the column

A system of linear equations is called consistent if it has at least one solution.

If the system has no solutions, it is called

Inconsistent

Let C be the coecient matrix for a consistent system of linear equations in

variables x₁, . . . , x_n.

(1) We say that x_i is a basic variable for the system if. . .

(2) We say that x_i is a free variable for the system if. . .

(1) We say that x_i is a basic variable for the system if the ith column of rref(C)

has a pivot.

(2) We say that x_i is a free variable of the system if the ith column of rref(C)

does not have a pivot.

A linear combination of vectors v₁, v₂ … , v_n in R^m is the vector of the form

…

where c₁, c₂, … c_n are scalars called coefficients of the linear combination

vector w = c₁v₁ + c₂v₂ + … + c_nv_n

The span of vectos v₁, v₂, … ,v_n in R^m is the set

…

That is span(v₁, v₂, …, v_n) is the set of all linear combinations of vectors v₁, v₂,… , v_n

span(v₁, … ,v_n) = {c₁v₁ + c₂v₂ + … + c_nv_n | c₁, c₂, …, c_n element of R }

A set of vectors {v₁,v₂,…,v_n} in R^m is linearly dependent if

…

otherwise the vectors are called linearly independent

if atleast one of the vectors is a linear combination of the others. That is, for at least…

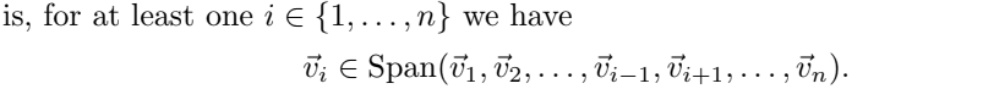
A vector space (over real numbers) in any set of vectors in R^n that satisfies all of the following properties

(1) v is non empty

(2) v is closed under addition

(3) v is closed under scalar multiplication

Let V be a vector subspace of Rⁿ. A spanning set (also known as a generating set) for V is…

any subset B of V so that v = span(B)

A subset B of a vector space V is called a basis if…

(1) B is a spanning set for V

(2) B is linearly independent

Let V be a nonzero vector subspace of R^n. Then, the dimension of V, denoted as dim(V) is…

equal to the size of any basis for V

The standard basis of Rⁿ is the set e := {e₁, e₂,…, e_n} where e_i is…

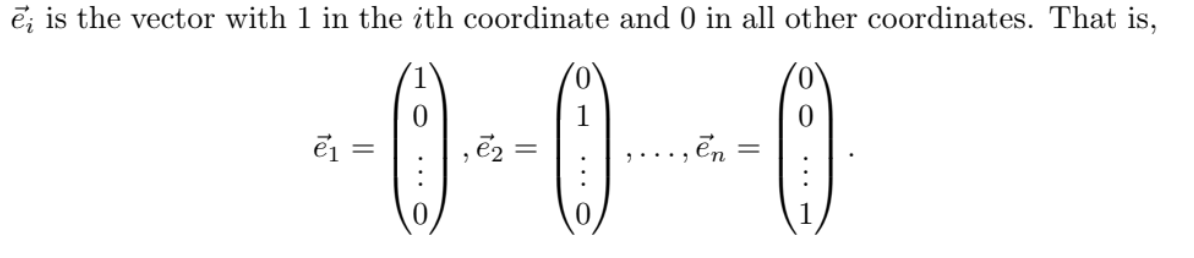
Let A be an mxn matrix with column vectors A = (v₁,v₂,…,v_n). Then for a vector x in Rⁿ , the matrix-vector product of A and x is the vector in R^m defined by…

Ax := x₁v₁ + x₂v₂ + … + x_nv_n

Let A be an mxn matrix. Then, the matrix transformation associated to A is the function…

A function F: Rⁿ → R^m is called Linear if it satisfies the following two properties for all vectors v,w element of Rⁿ and scalars c element R

(1) F(U + V) = F(U) + F(V)

(2) F(cU) = cF(U)

Let F: Rⁿ → R^m be a linear transformation. Then, the defining matrix of F is the m x n matrix M satisfying…

F(x) = Mx

A function f: X → Y is called one - to - one (or injective) if the following property holds…

for every y ∈ Y , there is at most one input x ∈ X so that f(x) = y. We often use the arrow f : X ,→ Y to indicate when a function is injective.

A function f : X → Y is called onto (or surjective) if the following property holds:

for every y ∈ Y , there is at least one input x ∈ X so that f(x) = y. We often use the arrow

f : X → Y to indicate when a function is surjective.

A function f : X → Y is called bijective if. . .

it is both injective and surjective

Let V be a subspace of Rⁿ and W a subspace of R^m. An isomorphism between V and W is

. . .

If an isomorphism exists between two vector spaces, we say these spaces are isomorphic, and we write V ~= W.

any linear bijective map F : V → W.

Let F: Rⁿ → R^m be a linear transformation

(1) The kernel F is the subset ker(F ) (= R^n defined by…

(2) The image of F is the subset im(F) (= R^m defined by …

Let F: Rⁿ → R^m be a linear tranformation.

(1) The rank of F is…

(2) The nullity of F is…

(1) The rank of F is the dimension of im(F)

(2) The nullity of F is the dimension of ker(F)

Let A be an mxn matrix with column vectors A = (v₁,v₂,…v_n).

(1) The column space of A is the subspace of R^m given by…

(2) The null space of A is the subspace of Rⁿ given by…

Let A be a matrix.

(1) The nullity of A is…

(2) The rank of A is…

(1) The nullity of A is the dimension of nul(A) and is denoted by nullity(A)

(2) The rank of A is dimension of col(A) and is denoted by rank(A)

A system of linear equations is called homogenous if…

the constant coefficients are all equal to zero

Let A = (v₁,v₂,…,v_n) and B = (w₁,w₂,…,w_n) be m x n matrices and c element of R be a scalar.

(1) The sum of A and B is the mxn matrix given by…

(2) The scalar product of A with c is the mxn matrix given by…

(1) The sum of A and B is the mxn matrix given by A + B := (v₁+w₁,v₂+w₂,…,v_n+w_n)

(2) The scalar product of A with c is the mxn matrix given by cA := (c₁v₁,…,c_nv_n)

Let A be an m x k matrix and B = (b₁,b₂,…,b_n) be a k x m matrix. Then the matrix product of A and B is the m x n matrix…

B = (Ab₁, …, Ab_n)

The identity matrix In is…

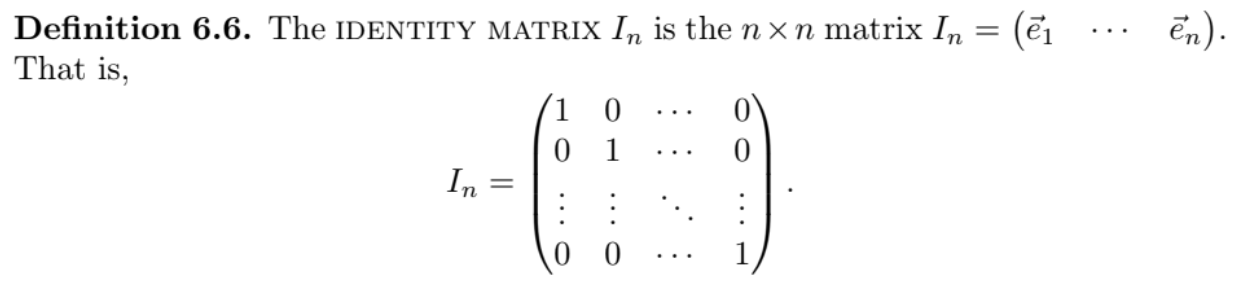
Let A be an n x n matrix. Then the inverse of A, if it exists is

is the matrix B so that AB = BA = In. In this case, we write B = A^-1

An n x n matrix is called elementary if…

it can be obtained by performing exactly one row operation to the identity matrix.

The unit square is the subset of R² given by…

S := {α₁e₁ + α₂e₂ : 0 ≤α₁,α₂ ≤1}.

An ordered basis {b₁, b₂} for R² is called positively oriented if…

we can rotate b₁ counterclockwise to reach b₂ without crossing line spanned by b₂

Let F: R² → R² be a linear transformation. Then, the determinant of F, denoted by det(F), is…

If A is a 2×2 matrix, the determinant of A, denoted by det(A) is…

The unit cube is the subset of R³ given by…

C := {α₁e₁ + α₂e₂ + α₃e₃ : 0 ≤ α₁,α₂,α₃ ≤1}.

For an n x n matrix A = (A_ij), the ij-minor of A is…

the (n-1) x (n-1) matrix A_ij with the ith row and jth column deleted

Let A be the n x n matrix with ij-entry equal to a_ij. We define the determinant of A by the following cofactor expansion formula:

det(A) := a₁₁ det(A₁₁)−a₁₂ det(A₁₂) +···+ (−1)ⁿ⁺¹a_1n det(A_1n).

Let A be an n x n matrix. A non-zero vector v is an eigenvector of A if

…

The scalar λ is called an eigenvalue

there is a real number scalar lambda such that Av = λV

Let A be an n × n matrix with eigenvalue λ.

(1) The λ-eigenspace of A is the vector subspace of Rⁿ defined by…

(2) The geometric multiplicity of λ is…

(1) E_λ := Nul(A - λI_n)

(2) the dimension of the λ-eigenspace E_λ

For an n x n A, the characteristic polynomial of A is…

X_a(x) = det(A-XI_n)

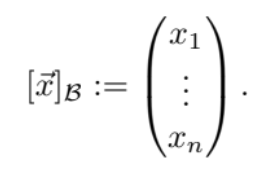
Let C and B be bases for a vector space V. Then, the change of basis matrix

M_C←B is the matrix satisfying

…

for every vector x in V

M_C←B[x]_B = [x]_C

Let F : Rⁿ → Rⁿ be a linear transformation, and B be any basis for Rⁿ. Then,

the defining matrix of F with respect to the basis B is the matrix M so that

…

We use the notation M = M_F,B

[F(x)]_B = M[x]_B

Two n x n matrices B and C are called similar if they represent the same function, but in possibly different bases. That is…

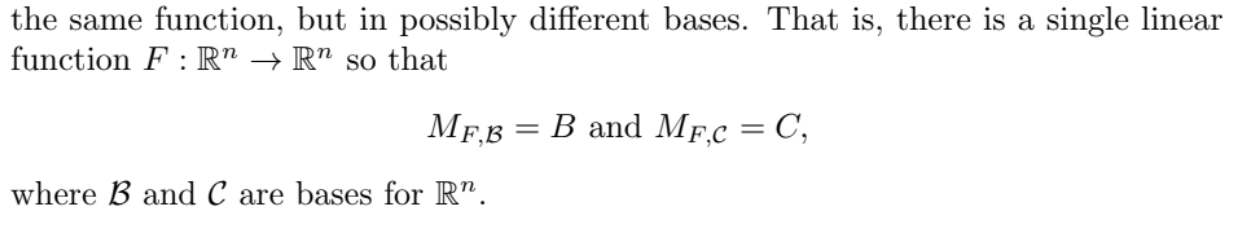
An n x n matrix D is called diagonal if

…

in this case we write D = diag(d₁,d₂,…,d_n)

the only nonzero entries in the matrix appear on the diagonal.

An n x n matrix is called diagonalizable if…

it is similar to a diagonal matrix.

Suppose that A is an n x n diagonalizable matrix with eigenvalues λ₁,…,λ_n and corresponding linearly independent eigenvectors v₁,v₂,…,v_n.

We call the equality. . .

the eigendecomposition of the matrix A. By diagonalization theorem, we know that…

(1) A = CDC^-1

(2) C = [v₁,v₂,…,v_n] and D = diag(λ₁,…,λ_n)

The dot product of u and v is the scalar

u * v = u₁v₁ + u₂v₂ +…+ u_nv_n

Let u and v be vectors in Rⁿ

(1) The norm of a vector u in Rⁿ is…

(2) The distance between vectors u and v is…

(3) We say that u and v are orthogonal if…

(1) ||u|| := sqrt(u * u)

(2) d(u,v) := ||u-v||

(3) u * v = 0

A basis B = {v₁,v₂,…,v_n} is orthogonal if

…

An basis B is orthonormal if it’s orthogonal and…

(1) v_i * v_j = 0 for every i not equal to j

(2) ||v_j|| = 1 for every v_j in B

We call an n x n matrix Q orthogonal if

…

Equivalently, Q is called orthogonal if Q^T = Q^-1

its column vectors form and orthonormal basis for Rⁿ

For vectors x,y in Rⁿ, the orthogonal projection of x onto y is…

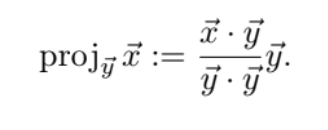
An n x n matrix A is called orthogonally diagonalizable if…

there exists an orthogonal matrix Q and a diagonal matrix D such that Q^TAQ = D

Suppose that A is an n x n symmetric matrix with eigenvalues λ₁,…,λ_n and orthonormal basis of eigenvectors {v₁,v₂,…,v_n}. We call the equality

…

a spectral decomposition of A, where…

(1) A = QDQ^T

(2) D = diag(λ₁,…,λ_n), and Q = (v₁,v₂,…,v_n)

Let A be an m x n matrix and {v₁,v₂,…,v_n} be an orthonormal basis for Rⁿ of eigenvectors for A^TA, as above. The singular values of A are…

{std}_i := ||Av_i||