module 8 rigid object rotations

s =

r∆­θ, where r is the radius, ∆θ is angular displacement, and s is the translational displacement

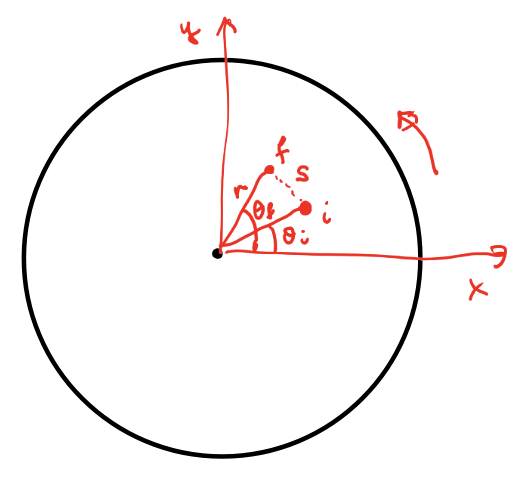
average angular speed

ω_avg = ∆θ/∆t , in units of sec^-1

angular acceleration

α , in units of sec^-2

angular velocity vector points

in direction of cross product (curl fingers in direction of rotation

x, v, and a for translational motion correspond to

theta, omega, and alpha for rotation = same kinematics equations

V_p moving along s =

rω

rotational radial acceleration =

rω²

rotational tangential acceleration =

rα

total rotational acceleration =

√(rα)² + (rω²)²

moment of inertia

I = Σ (i) (m_ir_i²) ; plays role of mass

rotational kinetic energy

½ Iω²

integral for moment of inertia

∫r²dm , where dm is usually density * dV

moment of inertia for a rigid rod about its centre

I = ML²/12

moment of inertia for a solid cylinder about its axis that makes sense

I = ½ MR²

parallel axis theorem

moment of inertia around a parallel axis = I_cm + MD² -

D is distance to the axis

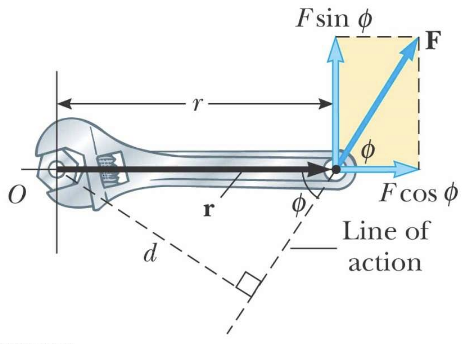
torque

τ (tau), analogue of force

τ =

rFsinφ = r x f (cross product) = Fd (d is perpendicular to the line of action)

net torque on a cylinder

T₂R₂ - T₁R₁

torque (second law application) =

Iα

rotational work =

τ • Δθ

rotational power =

rotational work/time or τ • ω

net work done by torque =

change in rotational KE

acceleration of a rolling object

Rα

kinetic energy of a rolling object

½ I_cm ω² + ½ mv_cm²

object rolling down an incline v_cm =

√2gh/1 + k ; where k is involved in I = kmR²