Linear

What is Ax = 0?

A homogeneous system where the output is zero.
- The set of all solutions forms a subspace.
- There is one solution (x = 0), which is the trivial solution. 
= Invertible 
- Finds null space

What is Ax = b?

A nonhomogeneous system. 
- Might have 0, 1, or infinitely many solutions only if b is in the column space of A. 

Rank

# of pivot columns 
- Tells you how much indpedence (linearly independent columns) the matrix has

Column Space: Col(A)

The set of all linear combinations of columns of A.
- It is a subspace of R^M (the output space).
- All vectors b for which Ax = b has a solution

Null Space: Nul(A)

It is a subspace of R^n (the input space)
- All vectors that the matrix sends to zero.

dim(Col A)

This is the rank.
- Tells you how many independent columns the matrix has. 

dimNul(A)

Tells you how many free variables there are when solving Ax = 0.

Rank-Nullity Theorem

rank(A) + nullity(A) = n
- Rank counts pivot columns
- Nullity counts free columns

Row Space: (Row(A))

The span of the rows of A
- dim(Row(A)) = rank(A)
- Row space tells you linear relationships among columns 
- Nonzero rows

m x n matrix

m = rows
n = columns

What is the range of T?

Column space of A

Invertible Matrix Theorem 

1. A is invertible
2. A has n pivots
3. Nul(A) = {0}
4. The columns of A are linearly indepdent
5. The columns of A span R^n
6. Ax = b has a unique solution for each b in R^n
7. T is invertible
8. T is one-to-one
9. T is onto
10. det(A) not equal to 0
11. 0 is not an eigenvalue of A.

Diagonalizable

The eigenvalue can show up more than once (AM > 1), but there also has to be more than one eigenvector for the same eigenvalue (GM > 1). 
- If GM < AM, then it is not diagonalizable 

Basis of a subspace

A set of vectors that satisfies two properties:
1. Linearly independent: none of the vectors are a combination of the other.
2. Spans the subspace: any vector can be written as a combination of the basis vectors. 
- Basis in R^m = finding Col(A)
- Basis in R^n = finding Nul(A)

Subspace

1. Zero vector in the subspace
2. Closed under addition
3. Closed under scalar multiplication 

Determinant

1. Row replacement does not change det(A)
2. Scaling a row multiplies the det by C.
3. Swapping two rows mutiplies the det by -1.
4. The det of matrix is equal to 1. 

Dot Product

The dot product of two vectors is a scalar.
1. Commutative: u*v = v*u
2. Distributive: u*(v+w) = u*v + u*w
3. Scalar multiplication: (cu)*v = c(u*v)
4. Self-dot gives legth squared: u*u = IIuII^2

Orthogonal Complement 

The orthogonal complement of V⊥ is the set of all vectors in R^n. 
- Orthogonal means perpendicular, so dot product = 0.

Orthogonal Projection

The orthogonal projection of a vector v onto a subspace W is the vector in W that is closest to v. 

Least Squares Solution

Solve a system of equations Ax = b that does not have an exact solution (inconsistent system). 
A^TAx = A^Tb

Counter-clockwise rotation by 90 degrees

(0 -1)
(1 0)

Reflection over the line y = x

(0 1)
(1 0)

Clockwise rotation by 90 degrees

(0 1)
(-1 0)

Reflection across the x-axis

(1 0)
(0 -1)
negate the y value

Codomain

R^m (output)
- Number of rows of A

Reflection across the y-axis

(-1 0)
(0 1)
negate the x value

One-to-One

For each y in R^n there is at most one x in R^m so that T(x) = y
- Pivot in every column

Onto

For each y in R^n there is at least one x in R^m so that T(x) = y
- Pivot in every row

(ColA)⊥ = Nul(A^T)

col(A) = Nul(A^T)⊥

Col(A^T)⊥ = Nul(A)

Col(A^T) = Nul(A)⊥

Domain

R^n (inputs)
- Number of columns of A

Linearly independent has __ solutions 

trivial

A linearly dependent system has __ solutions

nontrivial

A solution set with one free variable is a ___, two free variables is a __ 

Line, Plane

Span

All the linear combinations of a set of vectors 
- Set of solutions to Ax = 0

Linear combination of vectors

Combining vectors into one equation to produce a new vector. 

Determinant of a 2x2 formula

ad - bc

Inverse of A formula 

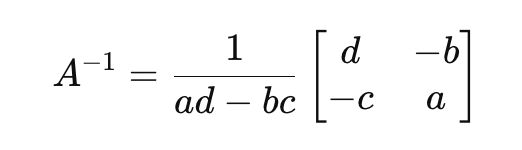
Characteristic Polynomial equation 

- Tr(A): (a+d)
- det(A): (ad - bc)

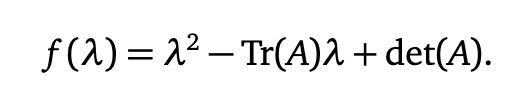
det(3AB^-1) = 1, det(A) = 2

(3^2)*2

EX) Write one vector c so that the orthogonal projection of v onto W is the zero vector

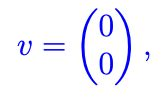
EX) Find the matrix B for orthogonal projection onto W formula. 

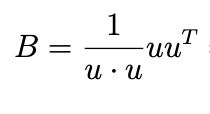
Find Xw formula. 

Xw = Bx

Find Xw⊥

X - Xw

To find dimensional subspace...

dim(colA) = pivots
dim(nulA) = free variables 
- subspace is the amount of columns 

To find W⊥ from Span...

Put in parametric vector form

Subspace

1. Zero vector in the subspace
2. Closed under addition
3. Closed under scalar multiplication 

Steady-State Vector formula

What are eigenvalues for 2×2 reflection matrix?

-1 and 1

What are eigenvalues for 2×2 projection matrix?

0 and 1