Algebra II Final Part 1: Functions

Includes domain, range, graphing functions, solving functions, function variable explanations, words problems, and definitions

Define: Function

An equation where an input (x) has a given output (y). An input can only relate to one output in a function, but different inputs can have the same output.

Define: Domain

All possible x values, or all possible inputs.
Written (lowest x)≤x≤(highest x)

Define: Range

All possible y values, or all possible outputs.
Written (lowest y)≤y≤(highest y)

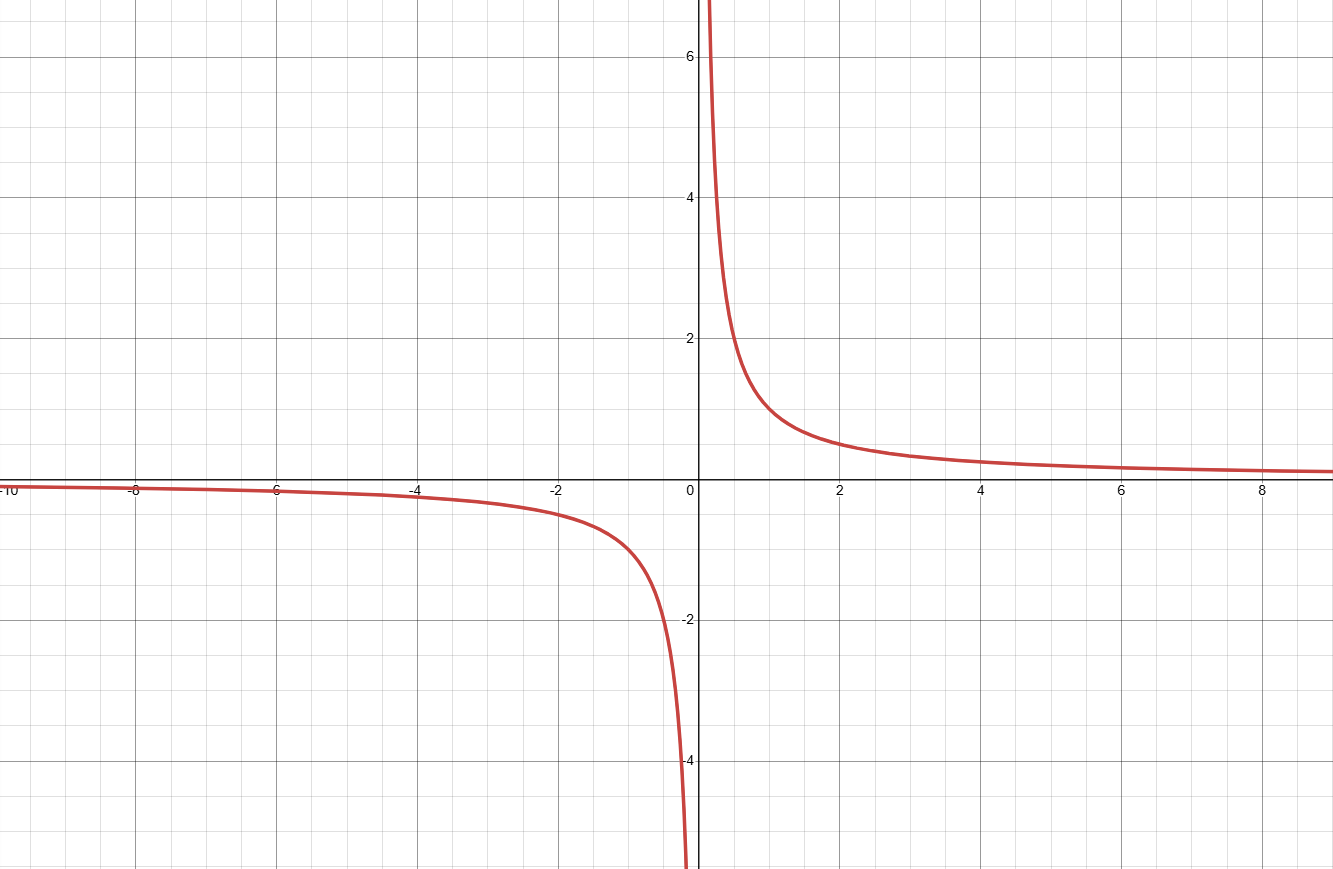
Sketch a graph: y=1/x

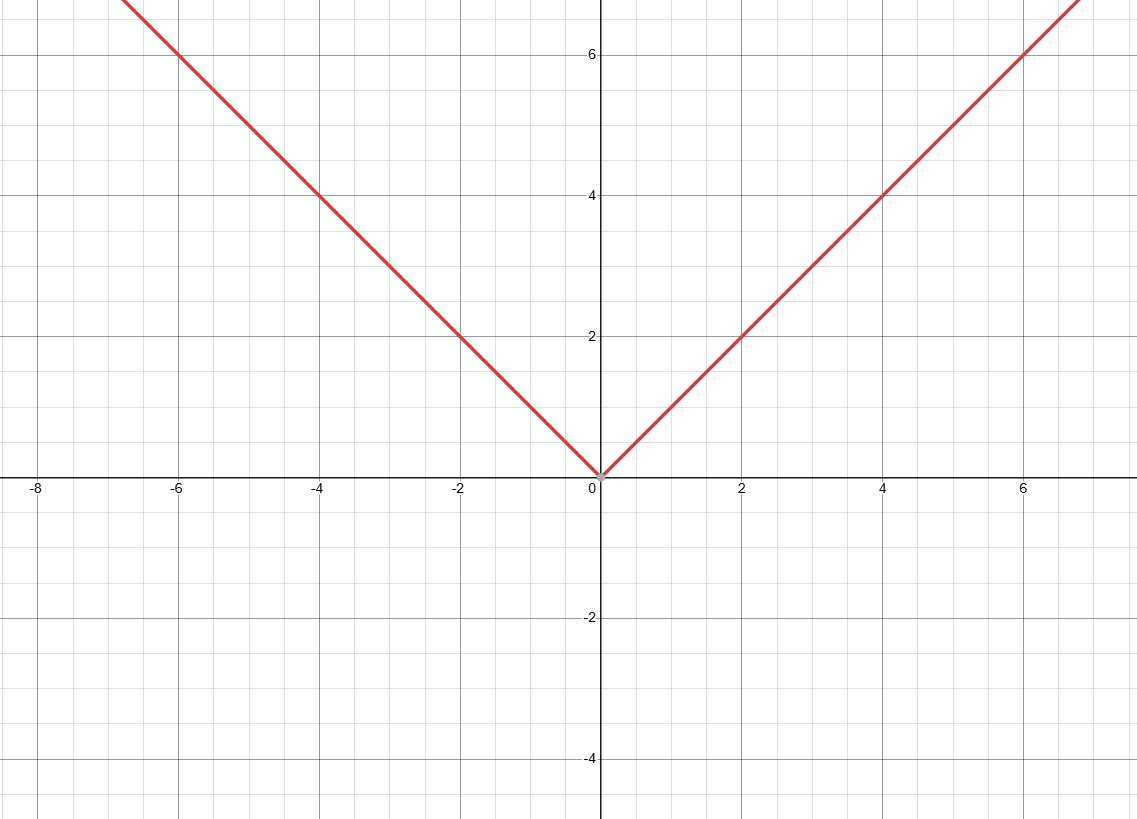
Sketch a graph: IxI

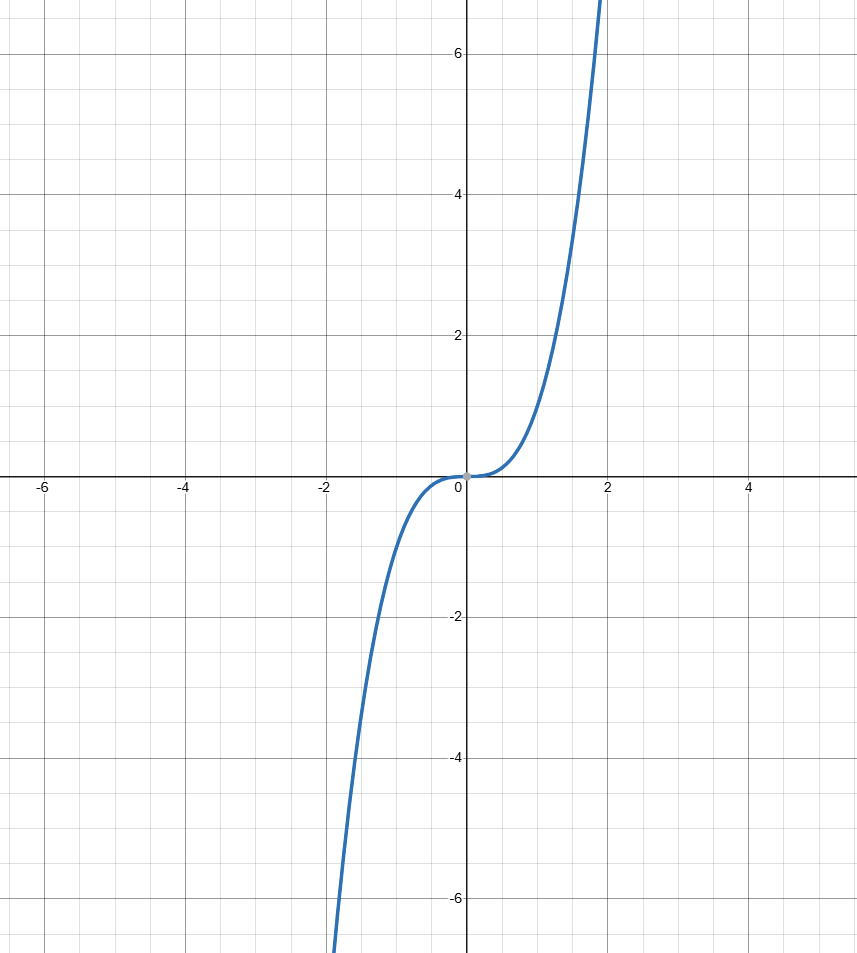
Sketch a graph: x³

Sketch a graph: with a horizontal asymptote

using y=2^x
Remember: A horizontal asymptote approaches a certain y value but never reaches it

Give the three forms of quadratic equations

Graphing/ Vertex form: y=a(x-h)²+k

X-intercept from: y=a(x-h1)(x-h2) (the numbers are subscripts)

Standard from: y=ax²+bx+c

Rewrite: y=x²+4x-3 in graphing form

y=(x+2)²-7

Rewrite: y=(x+5)²-4 in factored form

y=x²+10x-29 (I think, I can’t read y handwriting :/)

Create: An equation for a parabola in standard form

E.G: y=x²+5x+5

While watering her outdoor plants, Lettuce noticed that the water coming out of her garden hose created a parabola. She decided to model the water’s path with an equation based on some measurements she took. The highest point the water reached was 10ft, and it landed on plants 16ft away from her. The nozzle of the hose and the top of the flowers were 5ft above the ground. Create Lettuce’s equation.

y=-.078125(x-8)²+10

Step 1: sketch a graph with you points. We have the starting point of the water at (0,5), the vertex halfway at (8,10), and the top of the flowers at (16,5)

Step 2: Fill in the equation y=a(x-h)²+k with the known information, ending with 5=a(0-8)²+10.

Step 3: Simplify what you having, getting -5=64a (-5 from subtracting the 10 from the 5).

Step 4: divide -5 by 64 to get the value of a, getting -.078125

Step 5: Put together your final equation (see initial answer)

Plum and Apple are comparing their notes about graphing form. They both have similar examples, minus three differences:
-Plum’s parabola has a vertex 1 unit to the right of Apple’s

-Plum’s parabola has a vertex 2 units higher than Apple’s

-Plum’s parabola opens the opposite way.

Apple’s equation was y=3(x+3)²-5, but Plum didn’t write an equation because they are a silly billy. What was Plum’s equation?

y=-3(x+2)²-3

Marinated Beef’s parabola can be represented by mutiple equations, 2 of which are:

y=2(x+1)(x-3)

and

y=2(x-1)²-8

Which equation tells you the x-intercepts + state the intercepts

The first equation. The intercepts are (-1,0) and (3,0)

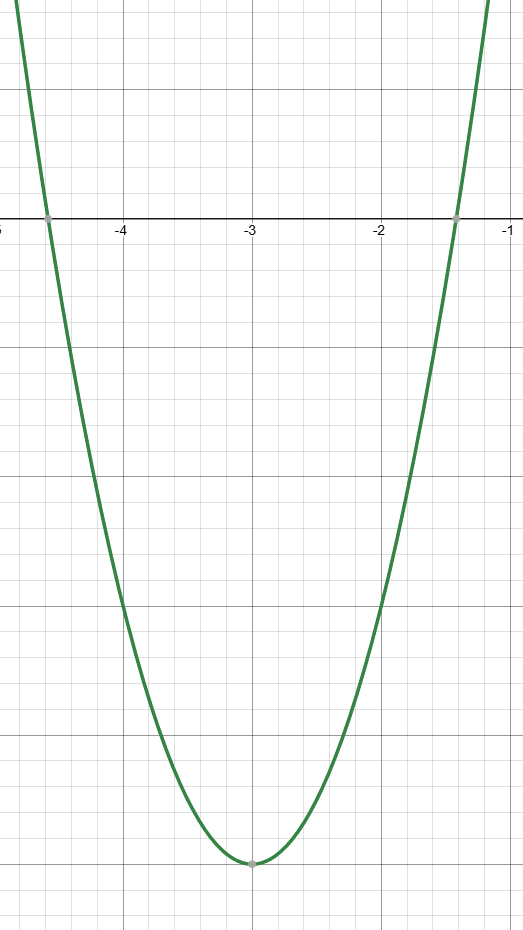
Give the equation of this graph in graphing form bc I don’t have it in the other forms

y=2(x+3)²-5