AP Pre-calculus S1 FINALS!!

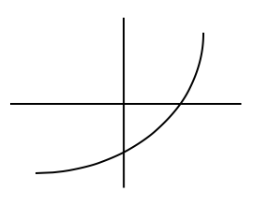
Graph of f

Graph of f is INCREASING ←→ Rate of change of f is POSITIVE

Graph of f is CONCAVE UP ←→ Rate of change of f is INCREASING

The graph of f is INCREASING at an INCREASING RATE

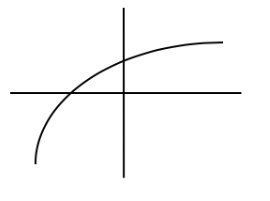
Graph of g

Graph of g is INCREASING ←→ Rate of change of g is POSITIVE

Graph of g is CONCAVE DOWN ←→ Rate of change of g is DECREASING

The graph of g is INCREASING at an DECREASING RATE

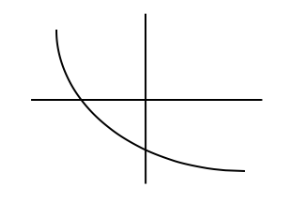
Graph of h

Graph of h is DECREASING ←→ Rate of change of h is NEGATIVE

Graph of h is CONCAVE UP ←→ Rate of change of h is INCREASING

The graph of h is DECREASING at an INCREASING RATE

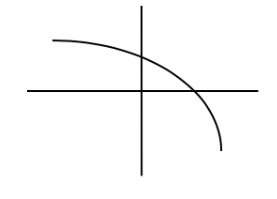
Graph of k

Graph of k is DECREASING ←→ Rate of change of k is NEGATIVE

Graph of k is CONCAVE DOWN ←→ Rate of change of k is DECREASING

The graph of k is DECREASING at an DECREASING RATE

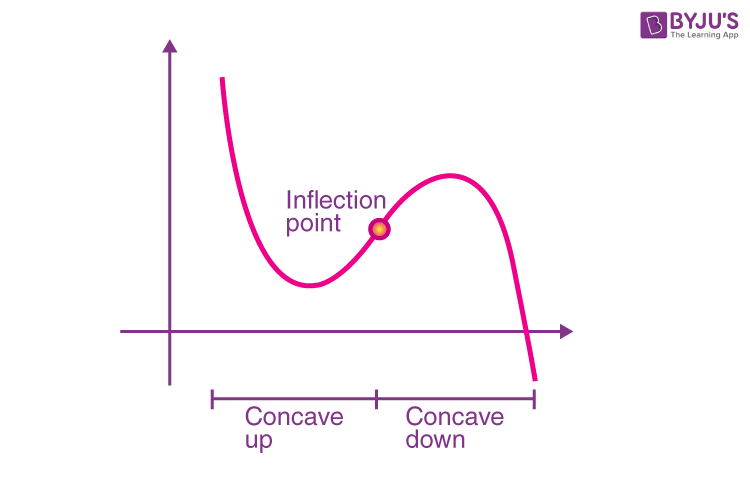
Points of inflection

Points where graph of f changes from concave up to concave down (or vice versa)

Average rate of change definition

slope between two points

The rate of change of f definition

slope of the graph at a single point

Average rate of change of a function over the interval [a,b] (a<x<b) is given by

AROC = f(b) - f(a) / (b-a)

Phrase to start a function explanation

“Over equal-length input-value intervals”

FUNCTIONS : if the differences in outputs are increasing, the function is ____

concave up

FUNCTIONS : if the differences in outputs are decreasing, the function is ____

concave down

FUNCTIONS : For a polynomial of the nth degree, the nth differences in output will be

constant

(quadratic function: 2nd differences are constant)

Complex Zeros

solutions (or roots) of polynomial equations that are complex numbers

Always comes in pairs!!!

If x=-2+4i is a zero, then so is x=-2-4i

Multiplicity

If a factor is repeated n times, it has a multiplicity of If

If a zero has an even multiplicity, the graph will bounce off the x-axis at that zero

The end behavior of a polynomial function is determined by

the leading term (highest degree)

What end behavior do you determine first?

Right and then left

Left end behavior

As x values decrease without bound, the y values of f(x)…

Even degree - goes in same direction as right

Odd degree- goes in opposite direction as right

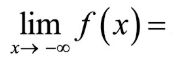
Right end behavior

As x values increase without bound, the y values of f(x)…

Leading term positive - y goes to infinity

Leading term negative - y goes to negative infinity

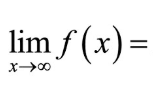
Even functions

Graphs have symmetry over y-axis

f(-x) = f(x)

Odd functions

Graphs have symmetry over the origin

f(-x) = -f(x)

Solving Polynomial Inequalities: -2(x+3)(x-1)²(x-4)<0

1. Put all terms on one side and factor

2. Create sign chart with all zeros marked

3. Check one value from each side of the zeros (far right interval usually easiest to check) for + or -

4. Each successive interval on the sign chart will alternate signs unless the zero has an even multiplicity

Zeros at = -3,1,4

Solution = (-inf, -2) u (4,inf)

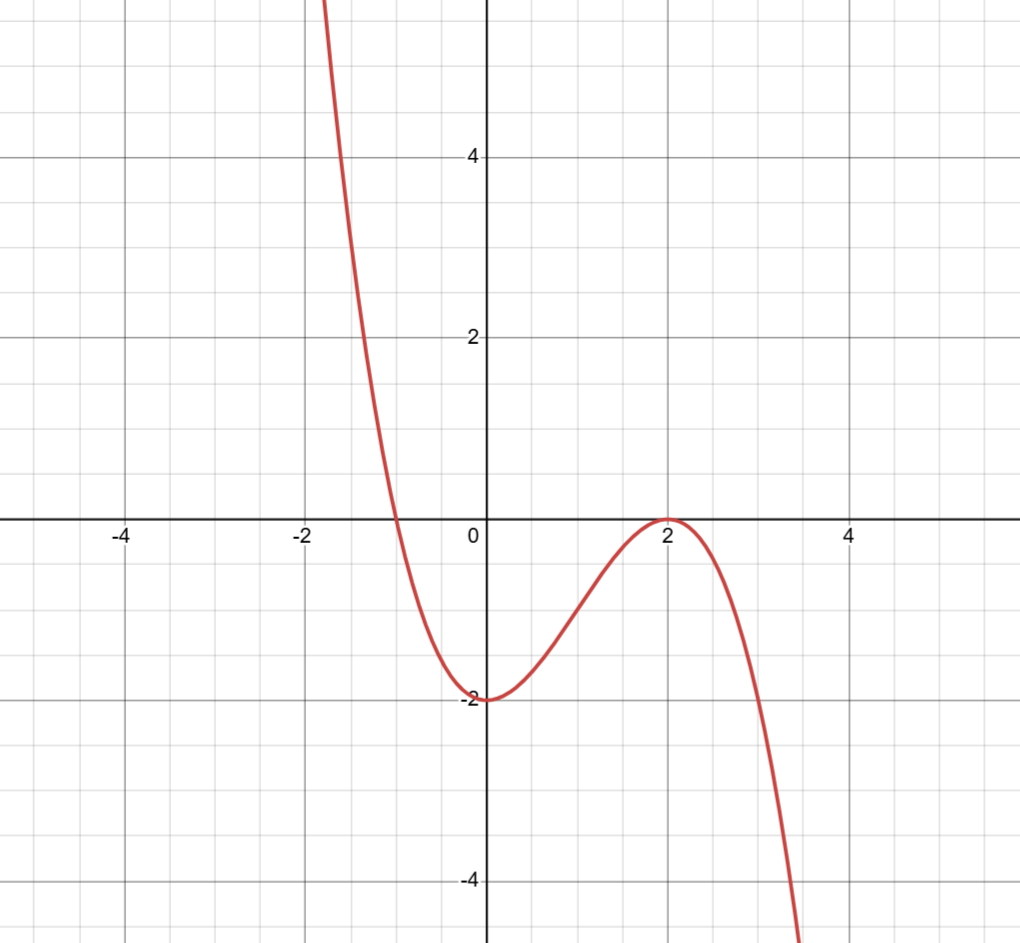
f(x) = -0.5(x+1)(x-2)²

Explain the properties of the graph and function

Zeros at x=-1 and x=2

Bounce at x=2 because (x-2)² has multiplicity of 2 which is even

Leading term = -0.5x³

Negative leading term → right side goes down

Odd degree → left opposite of right, left goes up

Left End Behavior = As x decreases without bound, the graph of f increases without bound

Right End Behavior = As x increases without bound, the graph of f decreases without bound

f\left(x\right)=\frac{x^4+x^3+5}{-2x^3-4x+1}

Find properties

N > D (Top Heavy)

No horizontal asymptotes

N = D+1 → Slant asymptote

End behavior → slanting line

y=\frac{x^4}{-2x^3}\to y=-\frac12x ← solve for slant/oblique asymptote

Left: \lim_{x\to-\infty}f\left(x\right)=\infty

Right : \lim_{x\to\infty}f\left(x\right)=-\infty

g\left(x\right)=\frac{-2x^3+3x+4}{5x^3-x+2}

Find properties

N=D (Same degree)

Horizontal asymptote

HA : y=\frac{-2x^3}{5x^3}\to y=-\frac25

End Behavior - Use horizonal asymptote

Left : \lim_{x\to-\infty}g\left(x\right)=-\frac25

“As inputs decrease without bound, the outputs become arbitarilty close to -2/5”

Right : \lim_{x\to\infty}g\left(x\right)=-\frac25

“As inputs increase without bound, the outputs become arbitrarily close to -2/5”

h\left(x\right)=\frac{2x^2+x-3}{x^4-x+2}

Find properties

N<D (Bottom Heavy)

Horizontal asymptote

HA : y=0

End Behavior - Use horizontal asymptote

Left : \lim_{x\to-\infty}h\left(x\right)=0

Right : \lim_{x\to\infty}h\left(x\right)=0

Rational Functions : Zeros

Numerator equals 0 AND denominator NOT equal 0

Rational Functions : Holes

Denominator equals 0 AND cancels out with the numerator (numerator has equal or larger multiplicity)

Rational Functions : Vertical Asymptotes

Denominator equals 0 AND does NOT cancel out with numerator (denominator has larger multiplicity)

r\left(x\right)=\frac{\left(x+5\right)\left(x+3\right)^2\left(x-1\right)\left(x-4\right)^4}{\left(x+3\right)^2\left(x-1\right)^2\left(x-4\right)^3}

Find zeroes, holes, and vertical asymptotes

Zero : x=-5

Holes : x=-3 + x=4

Vertical asymptotes : x=1

Factors in the denominator will never be a zero of the function.

Factors in the denominator always are a location of a hole or vertical asymptote

Limit Notation + In words (Verbally)

Left End Behavior

\lim_{x\to-\infty}f\left(x\right)=

The end behavior of f as x decreases without bound

Right End Behavior

\lim_{x\to\infty}f\left(x\right)=

The end behavior of f as x increases without bound

Arithmetic Sequence

Linear Functions

Sequence : a_{n}=a_{k}+d\left(n-k\right)

Geometric Sequences

Exponential Functions

Sequence : g_{n}=g_{k}r^{\left(n-k\right)}

Exponent Properties

b^{m}b^{n}

\left(b^{m}\right)^{n}

b^{-n}

b^{\left(\frac{1}{k}\right)}

b^{\left(m+n\right)}

b^{\left(mn\right)}

\frac{1}{b^{n}}

\sqrt[k]{b}

Exponential Functions are always…

increasing or always decreasing, and their graphs are always concave up or always concave down

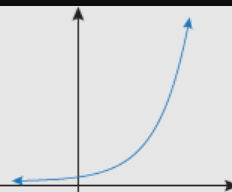
Exponential Function Property?

y=a\cdot b^{x}

a=1, b>1

Exponential Growth

Increasing at an increasing rate

\lim_{x\to\infty}ab^{x}=\infty

\lim_{x\to-\infty}ab^{x}=0

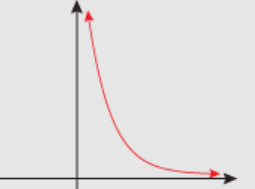
Exponential Function Property?

y=a\cdot b^{x}

a=1, 0<b<1

Exponential Decay

Decreasing at an increasing rate

\lim_{x\to\infty}ab^{x}=0

\lim_{x\to-\infty}ab^{x}=\infty

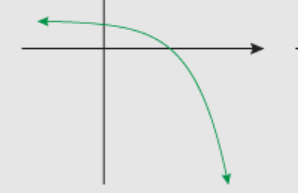
Exponential Function Property?

y=a\cdot b^{x}

a=-1, b>1

Exponential Growth

Decreasing at an decreasing rate

\lim_{x\to\infty}ab^{x}=-\infty

\lim_{x\to-\infty}ab^{x}=0

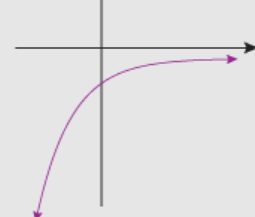
Exponential Function Property?

y=a\cdot b^{x}

a=-1, 0<b<1

Exponential Decay

Increasing at an increasing rate

\lim_{x\to\infty}ab^{x}=0

\lim_{x\to-\infty}ab^{x}=-\infty

Exponential function with natural base e is

f\left(x\right)=e^{x}

Additive and Multiplicative Transformations

g\left(x\right)=a\cdot b^{\left(cx+h\right)}+k

Vertical dilation by a factor of a units. If a<0, the graph reflects over the x-axis

Horizontal dilation by a factor of c units. If c<0, the graph reflects over the y-axis

Horizontal translation of -h units

Vertical translation of k units

Exponential Function Manipulation

f\left(x\right)=2^{x+3}

g\left(x\right)=3^{x-2}

y=9^{2x}

k\left(x\right)=9\cdot4^{x} (turn 4 →16)

f\left(x\right)=8\cdot2^{x}

g\left(x\right)=\frac19\cdot3^{x}

y=81^{x}

k\left(x\right)=9\cdot16^{\frac{x}{2}}

Every horizontal translation of an exponential function

f\left(x\right)=b^{x+h} is equivalent to

a vertical dilation of the exponential function

f\left(x\right)=ab^{x} where a=b^h

If a quantity doubles every day (d), then

f\left(d\right)=2^{d} gives the quantity after d days. An equivalent form,

f\left(d\right)=\left(2^7\right)^{\frac{d}{7}} indicates the quantity increases by a factor of 2^7 every week.

Regression Model : Residual Formula

Actual Value — predicted value

If the residual plot has no pattern,

the model is appropriate

Use a linear model when

the data reveals a relatively constant rate of change

Use a quadratic model when

the rates of change are increasing/decreasing at a relatively constant rate

Data generally follows a u shaped pattern

Use an exponential model when

the output values are roughly proportional.

Each successive output is approximately the result of repeated multiplication

What do inverse functions do?

they will “undo” a function. If you plug x into a function and then plug the output into the inverse function, we should end up with x again

Two functions are inverses only if

f\left(g\left(x\right)\right)=x and g\left(f\left(x\right)\right)=x

A continuous function will only have an inverse function if

it is strictly increasing or strictly decrasing

Log form of b^{a}=c

\log_{b}c=a

b>0, b does not equal 1

Common logarithm

Log base 10 = do not write the base

Log base e = write Ln instead

general form of logarithmic function

f\left(x\right)=a\log_{b}x

b>0, b does not equal 1, a does not equal 0

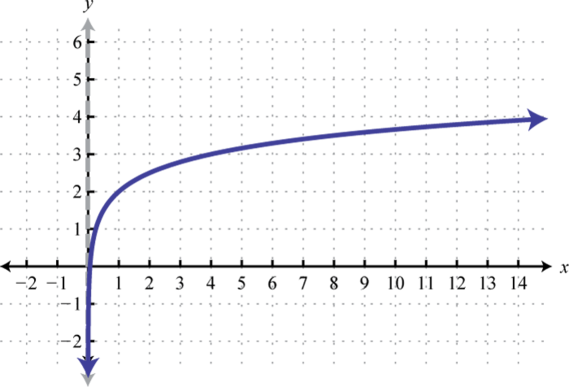
Logarithmic Property?

f\left(x\right)=a\log_{b}x

a>0, b>1

a does not equal 0, b does not equal 1, b>0

increasing at a decreasing rate

\lim_{x\to\infty}\log_{b}\left(ax\right)=\infty

\lim_{x\to0+}\log_{b}\left(ax\right)=-\infty

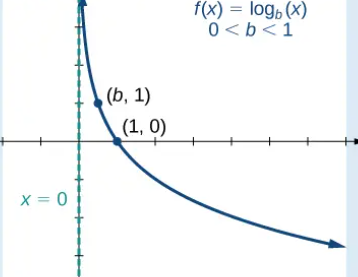
Logarithmic Property?

f\left(x\right)=a\log_{b}x

a>0, 0<b<1

a does not equal 0, b does not equal 1, b>0

decreasing at an increasing rate

\lim_{x\to\infty}\log_{b}\left(ax\right)=-\infty

\lim_{x\to0+}\log_{b}\left(ax\right)=\infty

Properties of Logarithms

\log_{b}\left(a\right)+\log_{b}\left(b\right)

n\log_{b}\left(x\right)

\frac{\log_{a}\left(x\right)}{\log_{a}\left(b\right)} where a>0 and a does not equal 1

\log_{b}\left(ab\right)

\log_{b}\left(x^{n}\right)

\log_{b}\left(x\right)