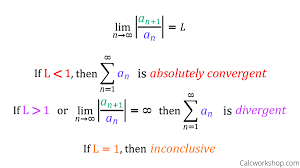Infinite Series

Improper Integral

A definite integral that has either, or both, limits infinite or an integrand that approaches infinity at one or more points; cannot be computed using the normal Riemann integral

Improper Integrals with Infinite Integration Limits

Goal: Create a limit question from the integral. Evaluate the limit after integrating

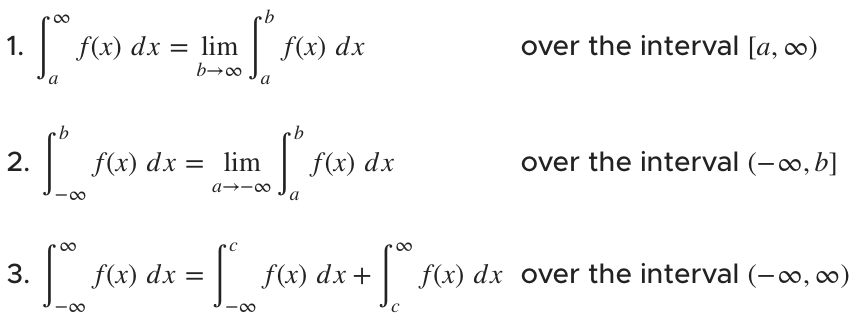
Integrals are considered CONVERGENT if

the limit exists and is a finite number (not positive or negative infinity)

Integrals are considered DIVERGENT if

the limit does not exist or is positive or negative infinity

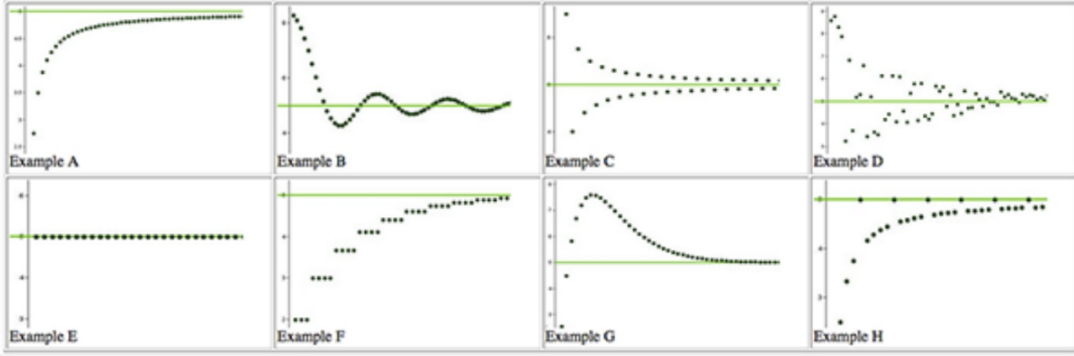
How do we determine if a Sequence Converges?

A sequence converges when it keeps getting closer and closer to a certain value

Sequences

A succession of objects or events in a specified order. In mathematics, it is used to describe an unending succession of numbers

Series

a sum of the terms of a sequence

Arithmetic Sequences

• Special type of Sequence

• Follows a pattern of adding a fixed amount(common difference) from one term to the next

Common Difference (d)

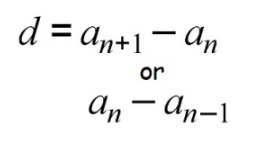
Explicit Arithmetic Sequence Formula

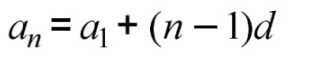
Recursive Arithmetic Sequence Formula

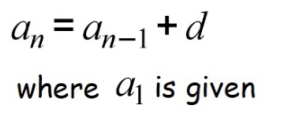
Geometric Sequences

• Special Type of Sequence

• Follows a pattern of multiplying by a fixed amount (common ratio) that’s not zero from one term to the next

common ratio r

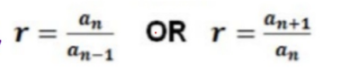
Explicit Geometric Sequence Formula

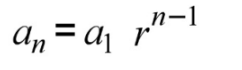
Recursive Geometric Sequence Formula

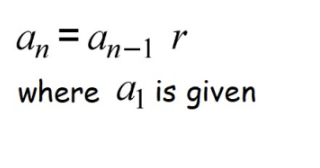
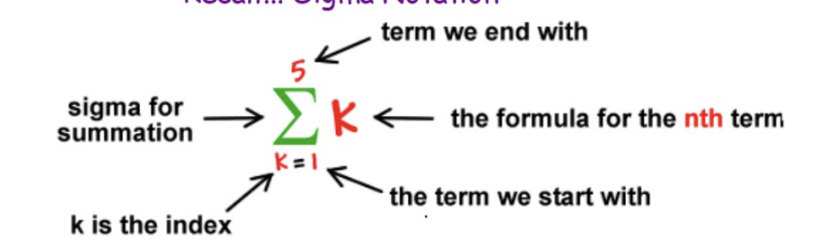
Sigma Notation

A Sequence is represented by..

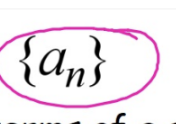
Finite Series

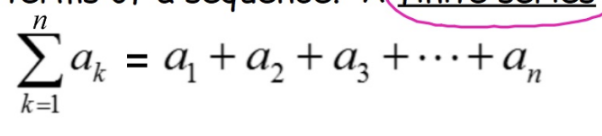
Infinite Sum

Infinite Series

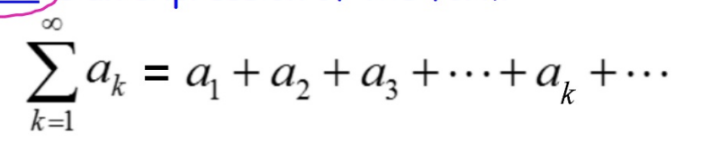
Limit of the Sequence

what to use to determine if a sequence converges or diverges, if the sequence has a limit, it converges to that value. If not, the sequence diverges

Power Series

A polynomial with an infinite # of terms

General Form of Power Series when centered at x = 0

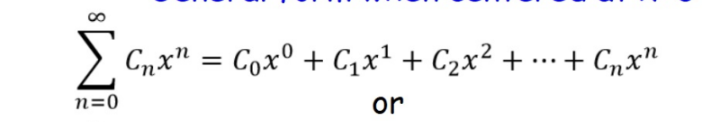
General Form of Power Series when centered at x=a (horizontal shift)

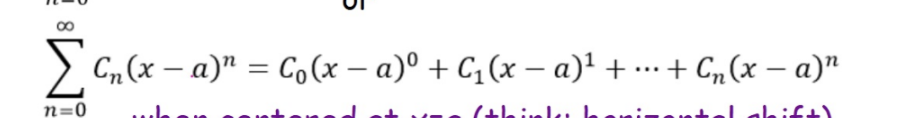
Taylor Polynomial

an expansion of a function into an infinite sum of terms, with increasing exponents of a variable like x, x²,.. and usually centered about an x value (x=a)

Maclaurin Polynomial

A special type of Taylor Polynomial where a=0

Taylor Series

Representation of Taylor Polynomial using Sigma Notation

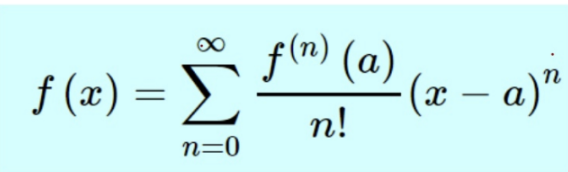
Maclaurin Series

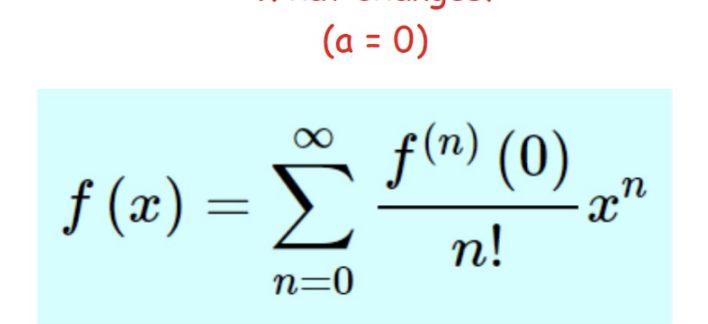
Two Key Questions about infinte series

1. Does the series converge?

2. If so, what is the limit? (In many cases we can’t answer this question)

First requirement of convergence of a infinite series

The individual terms must approach zero (they need to get smaller otherwise the sum will be infinitely large)

nth term test for divergence

Only tells if a series diverges not if it converges

Partial Sums Method

What helps us prove convergence since looking at the limit of the individual terms of a Series can only tell us if it diverges

Infinite Geometric Series

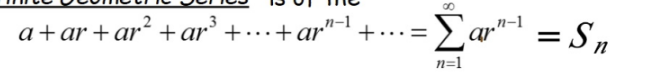
Partial sum of a geometric series

Geometric Series Test

P-Series Test

Harmonic Series

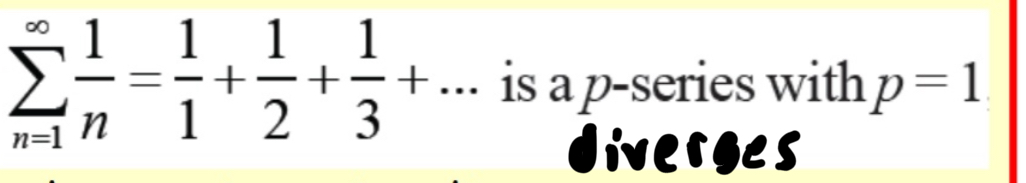
Difference between a p-series and a Geometric Series

Integral Test

Steps of Integral Test

Direct Comparison Test

Limit Comparison Test

Ratio Test