lecture 5 intraspecific population regulation

exponential growth model equation

dN/dt = (b-d)N = rN

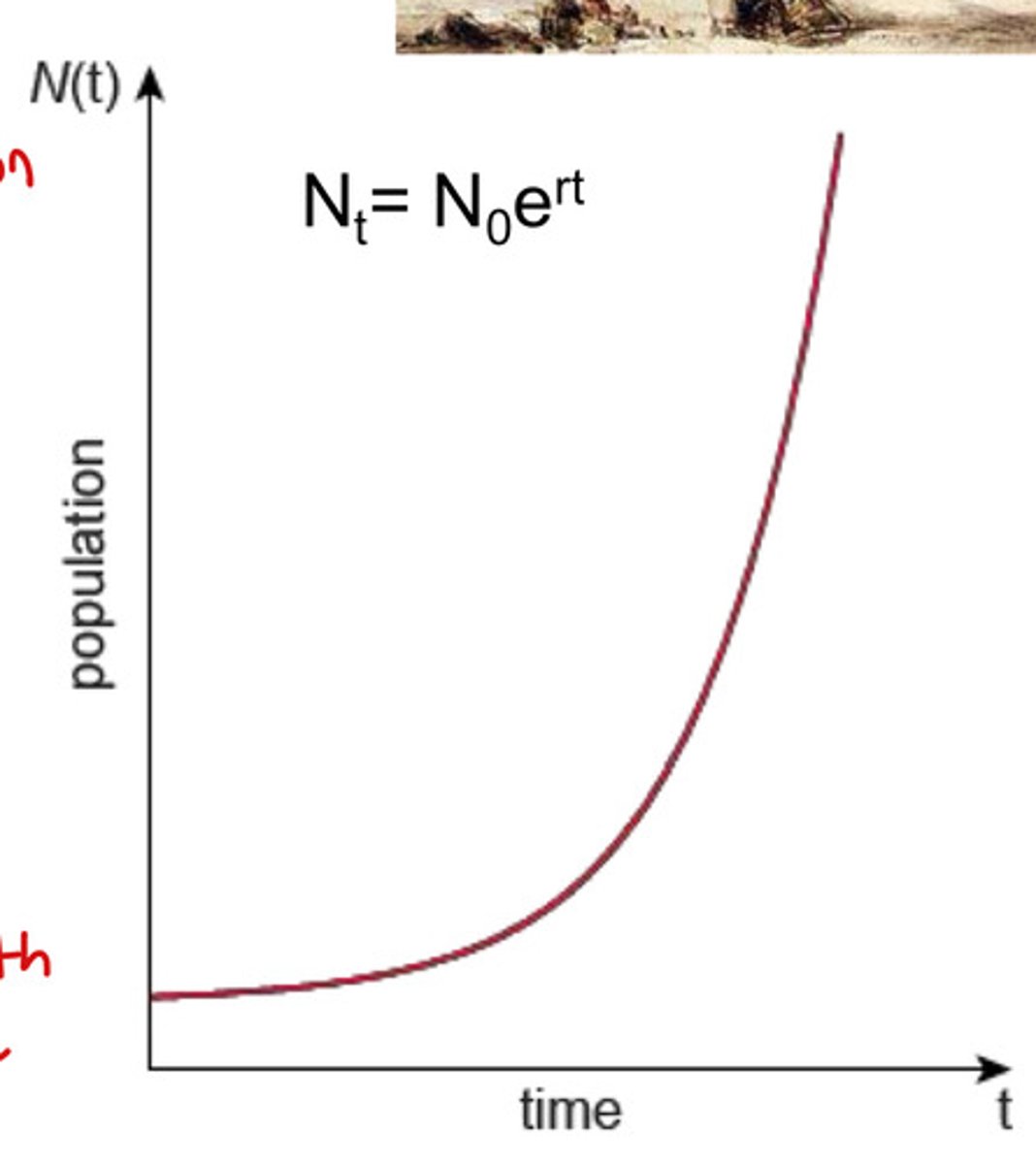
what are the assumptions of the exponential growth model?

1. infinite resources

2. constant birth and death rate

what do the terms in the exponential growth model mean?

dN/dt = (b-d)N = rN

dN/dt = instantaneous rate of change in population size ("growth rate")

r = intrinsic rate of increase

b = birth rate

d = death rate

N = population size

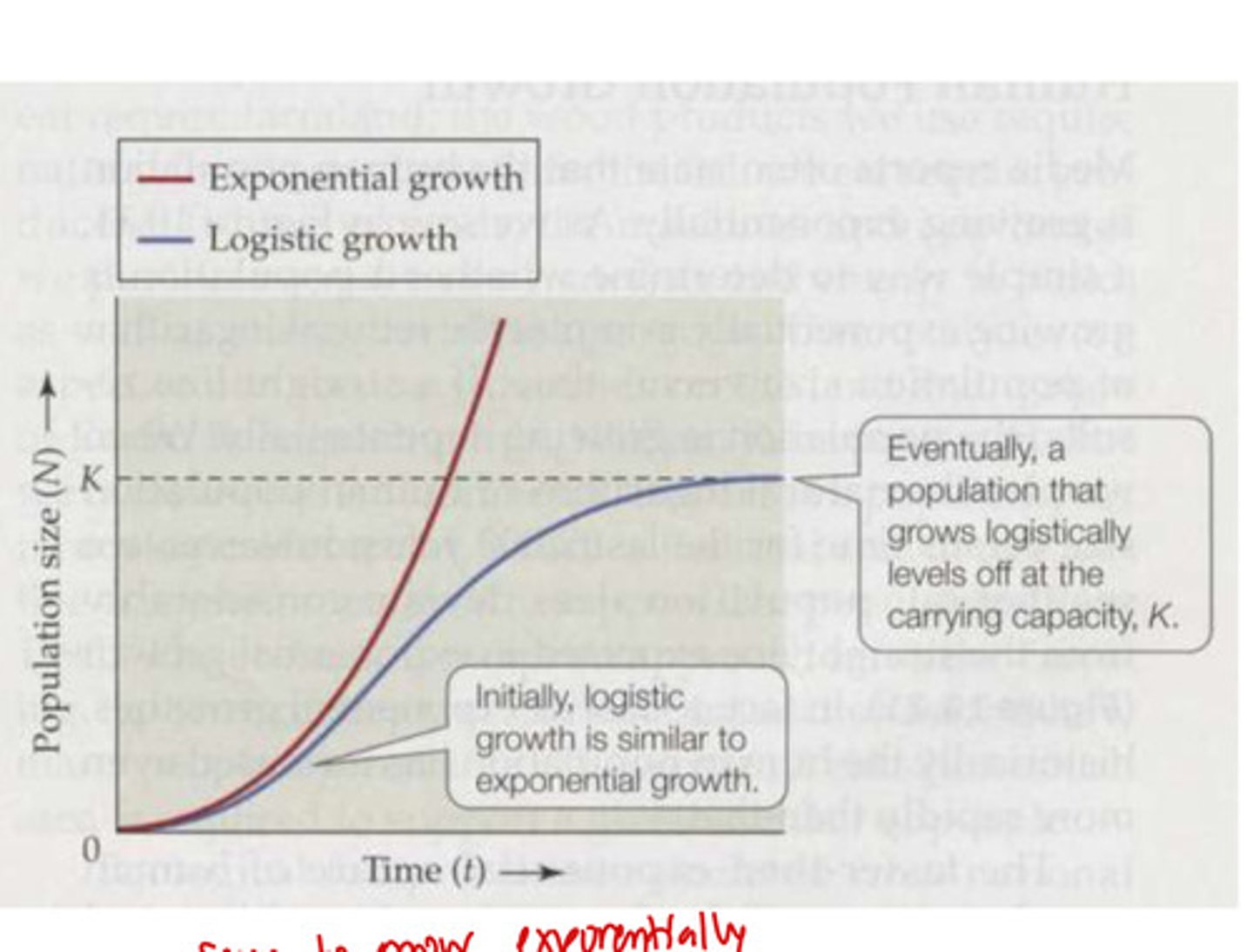
intraspecific population regulation

population growth is limited in natural populations because as population density increases, demand for limited resources increases, which increases competition

- limitations are imposed on population growth by other members of the same species (birth and death rate are not constant)

as population size (N) increases, what does the population experience?

increased mortality

decreased fecundity

actual birth rate formula

b = b0 - aN

d0 term meaning

minimum death rate

b0 term meaning

maximum birth rate under ideal conditions

when b > d what is happening to the population?

growing

when b = d what is happening to the population?

stable

when b < d what is happening to the population?

decaying

actual death rate formula

d = d0 + cN

what does slope c mean? slope a?

c = slope of death rate

a = slope of birth rate

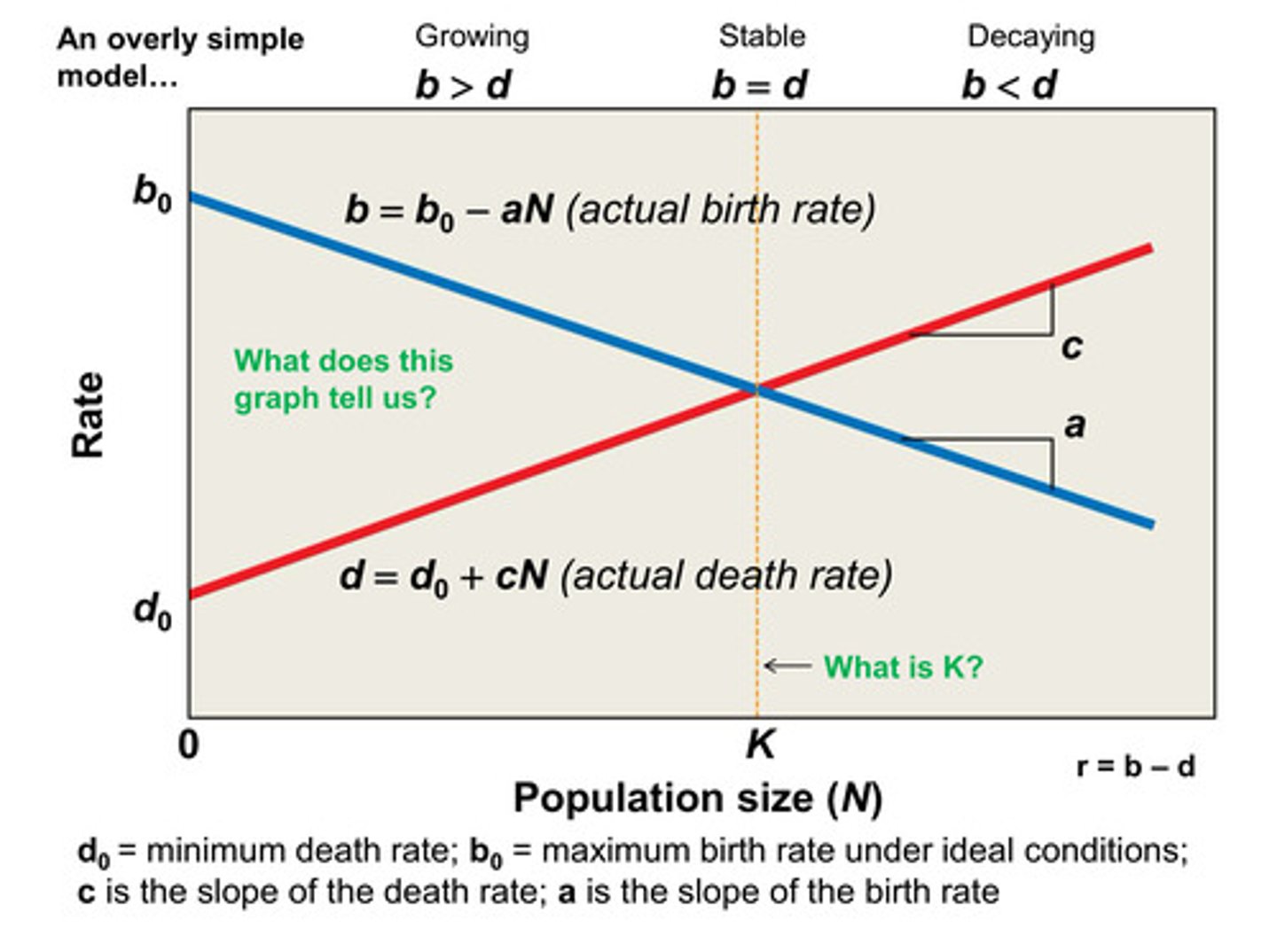
exponential population growth model including variation of birth and death rate as population changes

dN/dt = [(b0 - aN) - (d0 + cN)] x N

What happens as N increases according to this formula? dN/dt = [(b0 - aN) - (d0 + cN)] x N

as N increases, the birth rate declines and death rate increases, resulting in a slowing of population growth

K term meaning

carrying capacity

carrying capacity

the population size at which birth rate is equal to death rate is the maximum sustainable size in the current environment

maximum sustainable population size for a prevailing environment; can change

carrying capacity formula

K = (b0 - d0) / (a + c)

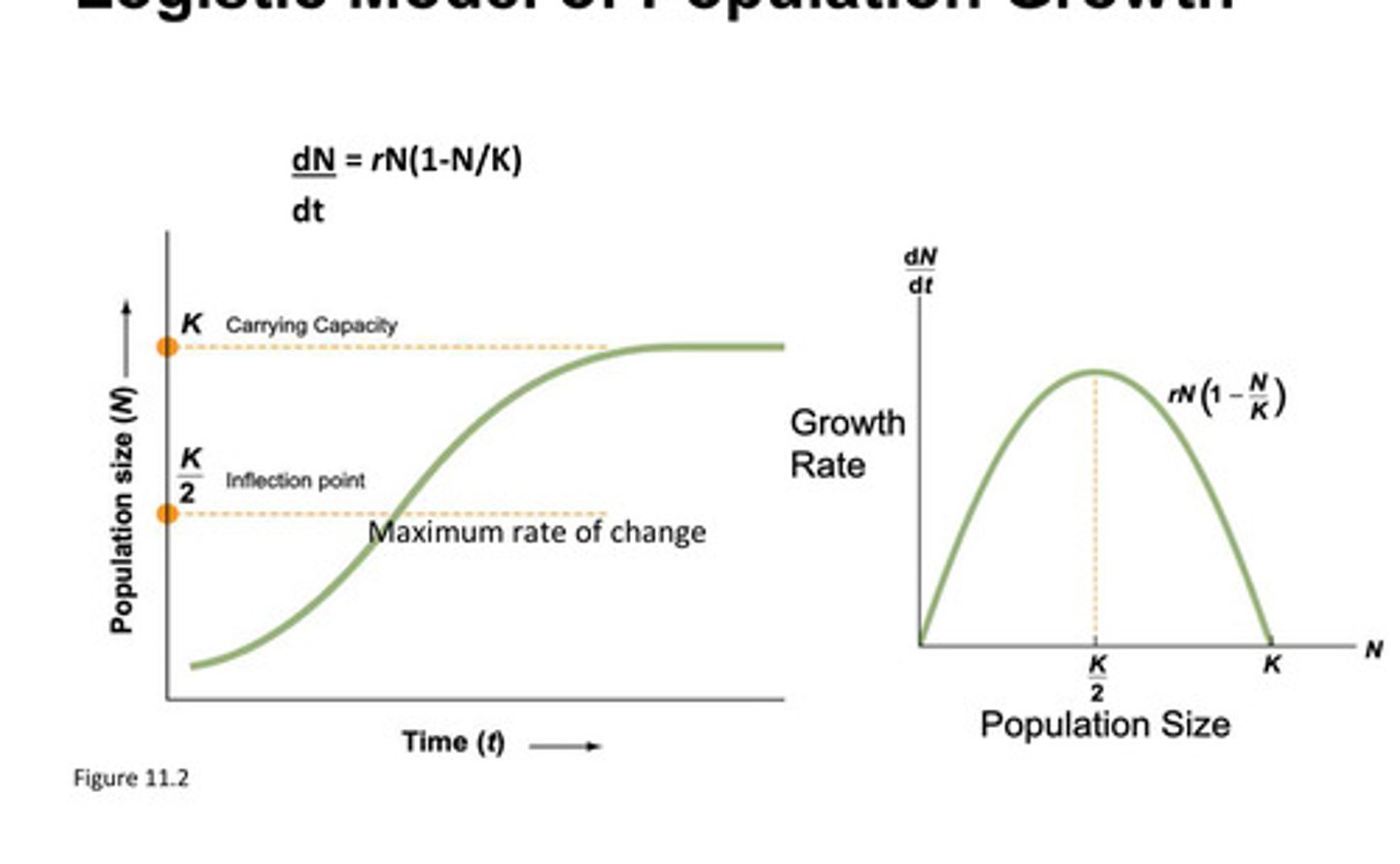
logistic model of population growth forumala

dN/dt = rN * (1 - N/K)

what does the rN term in the logistic model of population growth stand for?

exponential growth

- r is defined as a constant = b0 - d0

what does the (1 - N/K) term stand for in the logistic model of population growth?

slowing of population growth; reduction of population growth as the population approaches carrying capacity

what happens when N << K?

N/K approaches 1

close to exponential growth

what happens when N = K?

N/K is equal to 0

close to zero growth

what happens when N >> K?

N/K is negative

growth is negative

logistic growth in a population graph

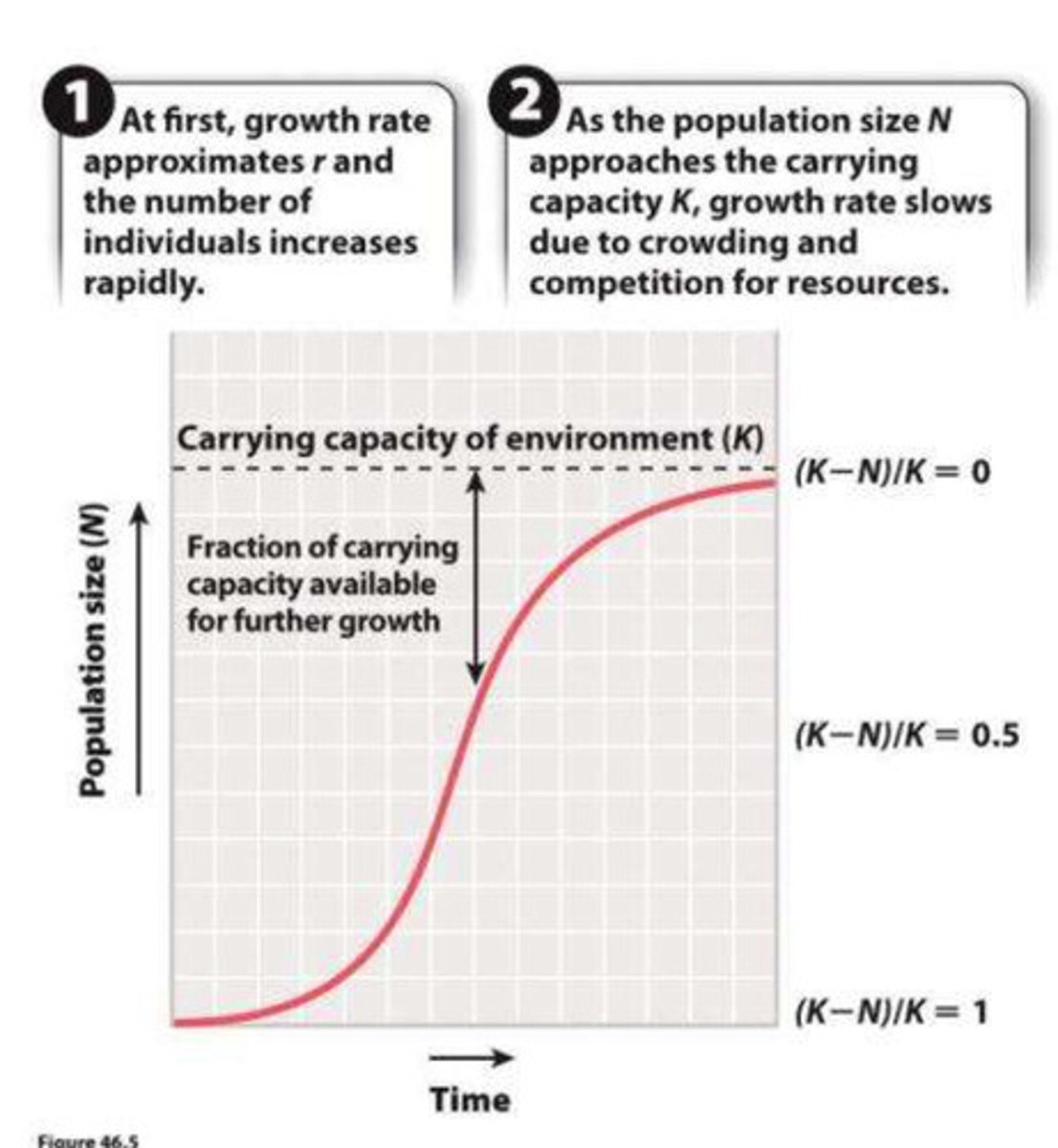
As N approaches K there is increased ______________ for limited resources

As N approaches K there is increased intraspecific competition for limited resources

labeled logistic growth in population graph

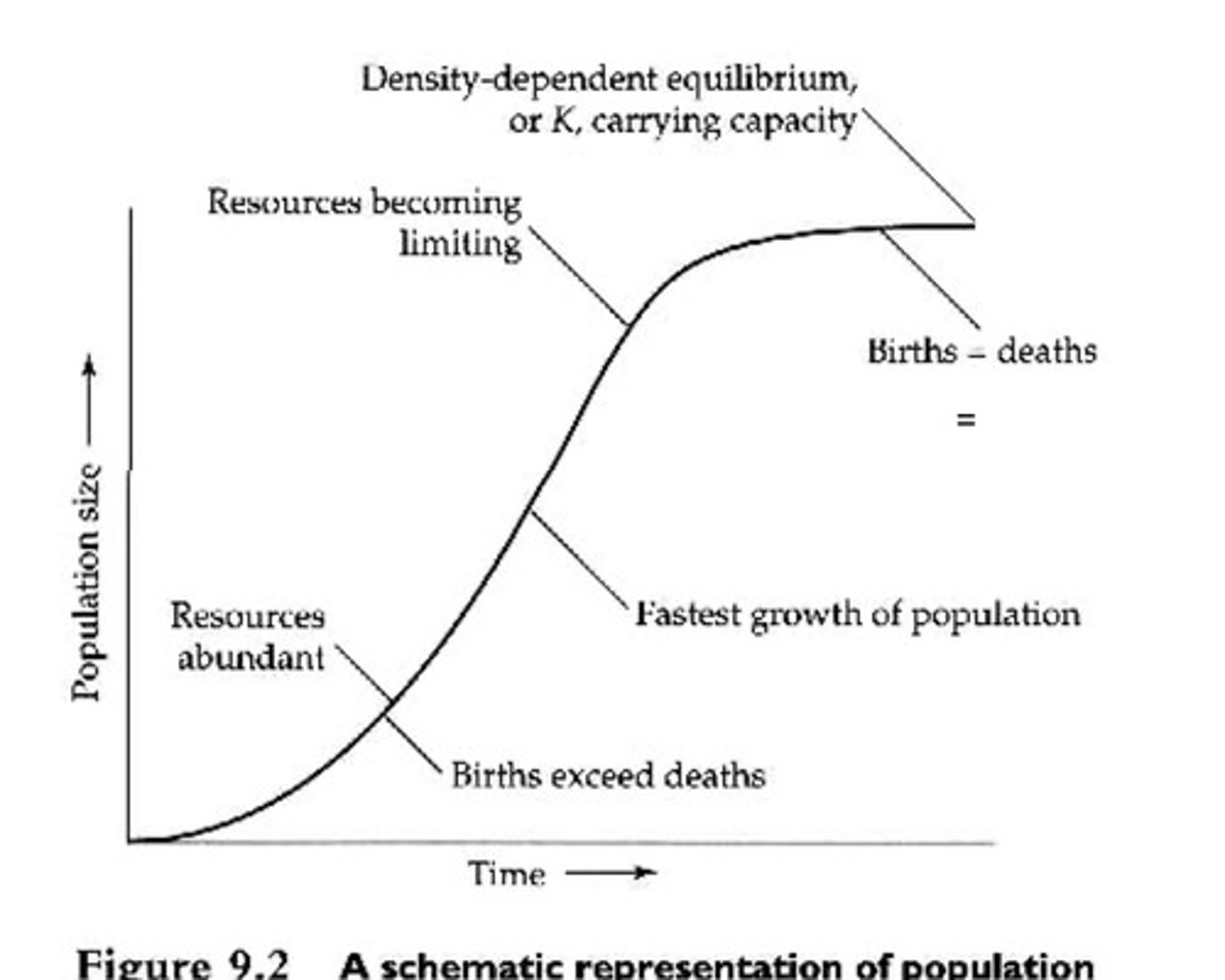
what happens if you go above the carrying capacity line?

the population overshot and got too large, so now it declines to go back to carrying capacity

K/2 term meaning

inflection point

what is the human carrying capacity?

1.5 billion people

density independent factors

factors not related to population density can influence birth and death rates within a population; are usually random

- examples: extreme weather events, flood, drought

density independent factors are associate to what kind of species?

r selected species

density dependent factors

things like competition for resources, disease, territoriality, intrinsic factors (physiological), predation, parasitism

density dependent factors are associated to what kind of species?

k selected species

density dependent mortality

as population density increases, the rate of mortality increases

density dependent fecundity

as population density increases, the rate of fecundity decreases

density dependent population regulation

- competition is density dependent

- competition generally slows growth and development, raises mortality rates, and reduces fecundity

- high density is stressful and can trigger hormonal changes that suppress growth, curtail reproduction, delay sexual activity, suppress the immune system

idea of sustainable yield

yield should not exceed the ability of natural population growth to replace harvested individuals

- manage population at intermediate population sizes

- take only those individuals that would naturally be lost to mortality

how is maximum sustainable yield achieved?

by managing populations at a level where maximum growth occurs

- in the case of the logistic model, this occurs at a population size N = K/2