Asset pricing

Asset pricing part of the course

Arbitrage.

1. What is the definition of an arbitrage?

2. What does no-arbitrage meaN?

1. Guaranteed profit by buying and selling assets simultaneously to take advantage of price discrepencies

2. Means there should not be an opportunity to make a risk-free profit, and prices should thus allign.

1. What is a Interest forward contracts

2. What is Yield to Maturity?

1. A contract where you can lean or loan amount x in period (n-1), at the forward interest rate r_f, which then has to be repaid (paid) at n.

2. Is the annulizaed rate of return and investor would earn if the lend the money out in the whole period, such:

(1+YTM)^n = (1+f1)(1+f2)…(1+fn)

Diversification.

1. What is the formula for the variance of a 2 asset portfolio

2. What is the benefit of diversification?

3. What is systematic risk?

4. What is idiosyncratic risk?

5. For which does investors require compensation from?

1. V(X+Y)=V(X)+V(Y)+2Cov(X,Y)

2. The lower the covariance, the lower the variance.> If we can add assets that are negatively correlated, we can reduce the variance.

3. It is the risk faced by all assets and cannot be avoided.

4. Firm-specific risk that can be diversified out of.

5. Only the systematic risk, as otherwise there would be an arbitrage opportunity,

Portfolio of investment:

1. What is the formula for the expected net return?

2. What is the formular for the variance?

1. The expected return is E(R) = x^T*b. Where

   1. R is scalar

   2. x is a vector of portfolio weights

   3. b is the vector of these N returns

2. The variance is: V(R) = x^T*A*x

   1. Where A is the variance-covariance matrix

CAPM I:

1. What is CAPM?

2. What question does CAPM attempt to answer?

3. What assumptions do we make?

4. What beliefs do Investors hold?

1. It is a financial model that establishes a relationship between the expected return and the systematic risk.

2. How to choose optimal portfolio weights to maximize expected returns at a given level of risk.

3. Not all risky assets have identical returns. And A has full rank.

4. Hold belief in the joint probability distribution of b and A.

CAPM II:

1. Is there any constraint on the portfolio?

2. What is the solution to the problem?

3. What is the efficient frontier?

1. There is no constraint; we can short-sell and asset.

2. A rational investor should choose a combination of assets that maximize the expected return given the desired risk level.

3. All the portfolio that desires 2.

CAPM III:

1. What is the Minimum Variane portfolio?

2. What is the formular?

1. The portfolio of asset x that minimiza the variance of the portfolio

2. See picture:

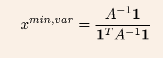
CAPM: General Efficiency Problem.

1. What is the efficient frontier?

2. How do we find the efficient frontier?

3. What is the Two mutual fund theorem?

1. The goal is the find max return to min risk, for any given R.

2. We minimize the var under the constraint that R=b^T*x

3. Once we have two efficient portfolios with different returns, we can find the entire efficient frontier by a linear combination of those two portfolios.

CAPM: Risk-free assets

1. What the assumptions about the return and variance of the risk free asset?

2. What is the slope of a portfolio combining the risk-free asset and risky assets?

3. What is this line called?

1. The expected return is r_f and the variance is 0.

2. The slop is given as: (E(r_i)-r_f)/(sqrt(V(r_i).

3. This is the Sharpe Ratio

CAPM: Sharpe-ratio

1. What is the Sharpe Ratio?

2. Can a portfolio have a higher sharpe ratio than the CML?

3. What is the CML?

1. The sharpe ratio is the slope value of the CML.

2. No, since the would imply assets with excees return compared to the market portfolio. The assets would then we added to the market portfolio.

3. It is the combination of risky and risky-free assets that all investors hold.

CAPM: Beta

1. What is beta?

2. What is the formular for Beta?

3. What is the formular for the CAPM pricing equation?

4. What does it say?

1. Beta is measures the risc of an assets compared to the market, and determines the risk premium on the given asset.

2. beta = cov(return from asset, return from market).

3. E(r_i)=r_f +beta*(E(r_m-r_f).

4. The higher beta, the higher return would an rational investor demand for adding it to the portfolio

CAPM: Security Market Line (SML)

1. What is it?

2. What does a higher/lower beta imply?

3. What happens if a stock has a higher/lower alpha than the SML?

1. Is it relationship between the expected return and the beta of a stock.

2. The higher the beta the higher expected return (visa versa).

3. If a stock is below the SML, it has a negativ alpha, and has lower returns compared to what CAPM determines, i.e. short the stock.

CAPM: practical in Excel.

1. How do we find the tangent portfolio?

2. How do we find the efficient frontier?

3. How do we find the capital market line?

1. We let z = A^-1*(b-r_f*1). Z = sum(z). Then x = z/Z.

2. The effiicente frontier is then found as alinear combination of the 2 portfolios.

   1. Let x be the weight of min var and 1-x be the weight of the efficiente portfolio.

   2. Find the weighs of each stock as. x*W_minvar + (1-x) * W_efficient

   3. Calculate properties.

3. The exact same as the efficient, just just the 100% in risk free instead of the min-var.

Properties of CAPM:

1. How do investors with heterogeneous preferences choose their portfolio?

2. Why in equilibrium the market portfolio is the efficient tangent portfolio?

3. Portfolio choice when no risk-free asset is available

1. They combine the risk-free asset and the market portfolio (efficient tangent portfolio) based on their risk tolerance, allocating more to the market portfolio as their risk tolerance increases.

2. Homogeneous expectations and market clearing ensure all investors demand the market portfolio, which maximizes the Sharpe Ratio and lies on the efficient frontier.

3. Investors choose portfolios along the efficient frontier of risky assets, with risk-averse investors leaning toward the minimum-variance portfolio and risk-tolerant investors selecting portfolios with higher risk and return.

Alpha:

1. What is alpha?

2. What is formular for alpha?

1. The difference between a stocks expected return and its required return according to the SML.

2. See pic

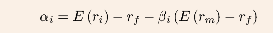
Alpha in relation to CAPM:

1. What does thet CAPM predict for alpha?

2. Why may there be some investors that earn alpha?

3. What can cause the possibility of alpha?

1. CAPM implies no alpha –> investors should choose the efficeint market portfolio and earn zero alpha.

2. A positive alpha is only possible if some other markets participants are willing to warn negative alpha.

3. Inefficiency (CAPM does not hold)

How to find Min var portfolio in Excel:

What are the steps?

1. Compute z = A^-11

2. Compute Z = sum(z)

3. Compute x = z/Z

Arbitrage pricing theory?

1. What is the idea?

2. What are the factors F_1,…,F_K?

3. Is arbitrage trades possible?

1. That CAPM does not caputure all risk factors thourgh beta, and instead we need more factors.

2. A factor is just a given risk meaures, beta is one for instance.

3. Yes, it can be.

Factor model - matrix notation

1. What is the equation for the factor model?

2. What is r?

3. What is F?

4. What is epsilon?

5. What is alpha?

6. What is B?

1. The equation is: r = a + B *F + epislon

2. The returns r_i in the column vector r.

3. List all factors is the column vector F.

4. List the disturbances epsilon in the column vector.

5. List all the intercepts in alpha.

6. List the factor loadings \beta_ik

7. List of factor loadings beta_ik. in the I X K matrix B.

Arbitrage pricing theory

1. When is the arbitrage possible in factor models?

2. What are the conditions in Matrix form?

1. No net position in assets, secured no risky profit so y_i*alpha_i > 0. For every k yi*b_ik = 0.

2. y^T1=0. y^Talpha>0 and y^TB=0^T

Arbitrage pricing theory

1. What is pure factor portfolio?

2. How do we solve for them?

3. How do we solve for risk free portfolio?

1. A combiniation of factor models, such that the portfolio only relies one-to-one on one factor.

2. We choose a selected factor and solve (see pic).

3. Exact same thing just 0^T instead of e_k^t

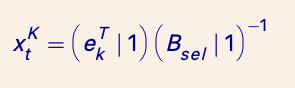
Factor risk premiums

1. The risk premium for factor k is what?

2. What is the expected return on our pure factor portfolio?

3. How can we price assets through asset risk premiums

1. Is denoted \lambda, and is the expected return on our pure factor portfolio minus the safe return.

2. It just \lambda + r_f.

3. Split portfolio in each pure factor portolio and rest in risk free portfolio. We can then replicate any systematic return i. And with no-arbitrage they should have the same return.

Arbitrage Free Pricing (AFP):

1. What does it do?

2. How does it differ from APT and CAPM?

3. How many possible assets and States are there?

4. What are the current price?

1. da

2. Model focus on asset prices rather than returns, thus no limits on weights.

AFP: Portfolio

1. What does a portfolio consist of?

2. What is the price of the portfolio now?

3. What is the future value of the portfolio?

4. What is the matrix V?

1. A portfolio consist of xi quantites of asset i.

2. The price of the portfolio now is xi * pi

3. The future value of the portfolio is x^TV

4. The matrix V, list the value of all assets in alle J states (I X J) matrix.

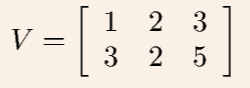
AFP: How is this matrix interpreted? (see picture)

1. How many states are there? How many assets?

2. What are the value in the different states of asset 1?

3. What are the value of the different states of asset 2?

1. There are two assets and 3 states

2. Asset one is worth 1 in state 1, and 2 in state 2 and 3 in state 3

3. Asset two is worth (3,2,5)

AFP: Arbitrage in this model of prics?

1. What are three conditions?

   1. x^Tp <= 0

   2. x^TV_j >= 0

   3. What is required of one of them?

2. What is type 1 arbitrage?

3. What is type 2 arbitrage?

1. The three conditions ensures arbitrage is possible.

   1. Today the cost of the portfolio is none-positive

   2. In all future states j, the portfolio ives a non-negative payoff

   3. At least one of the J + 1 inquelities above are strict (>/<). Such that you either earn now or in the future state

2. Type 1 arbitrage is earn a profit in the future

3. Type 2 arbitrage is earn a profit now

AFP: Replication:

If the value of an asset i in all future states can be replicated y a portfolio of y other assets.

1. What is the price of the asset to avoid arbitrage?

2. What happens if the price differs?

3. What happens if it is lower?

4. What happens if it is higher?

1. The cost of the replicating portfolio must equal the cost of the asset, ie.e. v = y^TV

2. If the price differs there is an arbitrage opportunity

3. Asset is cheaper than the replicating portfolio: Sell asset i and buy the replicating portfolio (Type 2)

4. Asset is more expensiv than the replicating portfolio: Buty assey i and sell the replicating portfolio (Type 1).

AFP: Fundamental theorem of asset pricing

1. What does it say?

2. What are state prices?

3. What are the formular for state prices

1. It is possible to find a J X 1 vector d_j > > 0, such that p = Vd if any only if the market is arbitrage free.

2. The value of one unit of CF in state J.

3. The formula is p = Vd or d = V^-1p