Conservation Laws in Physics to Know for AP Physics C: Mechanics (2025)
Conservation laws are foundational principles in physics that describe how certain quantities remain constant within closed systems. These laws—energy, momentum, angular momentum, mass, and electric charge—play a critical role in understanding and solving problems across various fields of physics, including mechanics, electromagnetism, thermodynamics, and quantum physics.
The following sections provide a formal explanation of each conservation law, supported by relevant examples and additional insights.
I. Conservation of Energy
The Conservation of Energy states that energy cannot be created or destroyed, but only converted from one form to another. In any closed system, the total energy remains constant. This law is fundamental to understanding how energy behaves in mechanical, thermodynamic, and other physical processes.
Key Concept: Energy can be transferred between different forms (e.g., from kinetic energy to potential energy), but the total energy in the system remains the same.
Principle: Energy cannot be created or destroyed; it can only be transformed from one form to another.
Description:
In a closed system where only conservative forces (e.g., gravitational force, spring force) are acting, the total mechanical energy (sum of kinetic and potential energies) remains constant.
In inelastic collisions, kinetic energy is not conserved as some of it is converted into other forms of energy such as thermal energy, but the total energy (including heat) remains conserved.
The work-energy theorem relates the work done on an object to its change in kinetic energy:
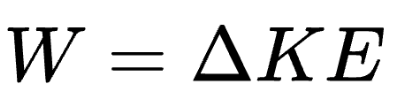
A pendulum exchanges potential and kinetic energy as it swings.
Roller coasters rely on energy conversion between kinetic energy (at the bottom) and potential energy (at the top).
Solar panels convert solar energy into electrical energy.
Additional Insight:
Energy conservation extends beyond classical mechanics into other areas such as thermodynamics and modern physics (e.g., mass-energy equivalence, E=MC²).
Work-Energy Theorem: The work done on an object is equal to the change in its kinetic energy. For example, if you apply a force to move an object, the amount of energy you put into the system directly increases its kinetic energy.
II. Conservation of Linear Momentum
The Conservation of Linear Momentum states that in an isolated system with no external forces acting on it, the total momentum remains constant. Momentum is the product of an object's mass and its velocity.
Key Concept: If no external forces (such as friction or an external push) are acting, the momentum before an interaction (like a collision) is equal to the momentum after the interaction.
Principle: The total linear momentum of a system remains constant in the absence of external forces.
Formula:
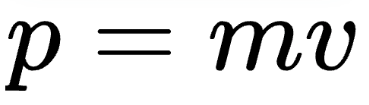
Where:
p is momentum
m is mass
v is velocity
Description:
In elastic collisions, both momentum and kinetic energy are conserved.
In inelastic collisions, momentum is conserved, but some kinetic energy is lost to other forms of energy.
Impulse is defined as the change in momentum, and it is related to the force applied over time insights.
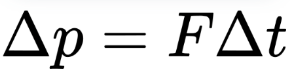
Examples:
In a rocket launch, the expulsion of gases backward results in the forward motion of the rocket, illustrating momentum conservation.
The recoil of a gun upon firing a bullet demonstrates the principle of momentum conservation in action.
Additional Insight:
The conservation of momentum is vital in various practical scenarios, including analyzing car crashes, sports physics, and particle collisions in high-energy physics.
III. Conservation of Angular Momentum
The Conservation of Angular Momentum states that if no external torque acts on a rotating object or system, the total angular momentum remains constant.
Key Concept: Angular momentum depends on an object's moment of inertia (how mass is distributed relative to the axis of rotation) and its angular velocity (how fast it is rotating). If the distribution of mass changes, the rotational speed will adjust to keep angular momentum constant.
Principle: The total angular momentum of a system remains constant if no external torque acts on it.
Formula:
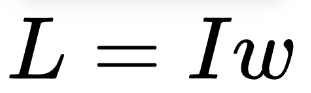
Where:
L is angular momentum
I is the moment of inertia
ω is angular velocity.
Description:
Changes in an object’s distribution of mass (e.g., a figure skater pulling in their arms) result in a change in rotational speed to conserve angular momentum.
Examples:
A spinning figure skater pulls in their arms and spins faster due to the conservation of angular momentum.
The Earth's rotation is gradually slowing over time due to the conservation of angular momentum and redistribution of mass.
Additional Insight:
Angular momentum conservation is a critical principle in astrophysics and is used to explain phenomena such as the motion of celestial bodies and the formation of planetary systems.
IV. Conservation of Mass
The Conservation of Mass states that mass cannot be created or destroyed in a closed system. The mass of the system before and after a reaction or process remains the same.
Key Concept: The total mass remains unchanged in chemical reactions or physical processes. Even though matter can change forms (e.g., from a solid to a gas), the total amount of matter remains constant.
Principle: Mass is conserved in a closed system; the total mass before a reaction or process is equal to the total mass after the process.
Description:
In chemical reactions, mass is neither created nor destroyed. The mass of reactants equals the mass of products.
In nuclear reactions, although the mass of particles may appear to change, the mass-energy equivalence (as expressed in Einstein's famous equation,E=MC²) must be considered.
Examples:
In a chemical reaction such as combustion, the total mass of reactants and products remains the same.
Food digestion involves a transformation of mass and energy but respects the conservation of mass.
Additional Insight:
Although mass conservation is assumed in classical mechanics, in relativistic contexts, mass is interrelated with energy, requiring the use of mass-energy equivalence in processes involving high velocities or extreme conditions.
V. Conservation of Electric Charge
The Conservation of Electric Charge states that the total electric charge in an isolated system remains constant over time. Electric charge can be transferred between objects, but the net charge within a closed system does not change.
Key Concept: Charge can be transferred from one object to another (e.g., rubbing a balloon on your hair), but the total amount of charge remains the same before and after the transfer.
Principle: Electric charge is conserved in an isolated system; the total charge before an interaction equals the total charge after the interaction.
Description:
Charge can be transferred between objects (e.g., when rubbing a balloon), but the total charge in the system remains unchanged.
In electric circuits, charge conservation ensures that charge entering a junction is equal to the charge leaving it (Kirchhoff's Current Law).
Examples:
Lightning results from the redistribution of charge between clouds and the Earth.
In electrochemical reactions (e.g., in batteries), charge is transferred between electrodes, yet total charge conservation is maintained.
Additional Insight:
Charge conservation plays a fundamental role in the study of electromagnetic interactions and is crucial for understanding phenomena in particle physics and electric circuits.
In electric circuits, the amount of charge entering and exiting a junction is always the same (Kirchhoff’s Current Law).
In particle physics, charge conservation is fundamental to understanding particle interactions and decays.
Importance of Conservation Laws in Physics
I. Universality: These laws apply universally across different scales, from subatomic particles to astronomical systems.
II. Simplification of Problems: Conservation principles allow for the simplification of complex systems, making it easier to solve real-world problems without having to track every individual force or interaction.
III. Interdisciplinary Connections: These laws link various branches of physics, providing a unified framework for understanding different physical phenomena.
These conservation laws provide powerful tools for solving a wide range of physical problems. They allow scientists and engineers to simplify complex systems and predict the behavior of objects in motion, the outcome of collisions, and the interactions between particles and forces.
Understanding and applying these laws helps to unlock the mysteries of the universe, from the motion of planets in space to the behavior of subatomic particles.
 Knowt
Knowt
