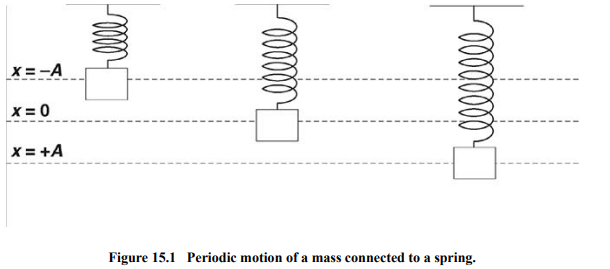
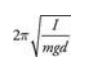5.0(1)
Other AP Physics C: Mechanics unit study guides
AP Physics C: Mechanics Ultimate Guide
Unit 1: Kinematics
Unit 2: Newton’s Laws of Motion
Unit 3: Work, Energy, and Power
Unit 4: Systems of Particles and Linear Momentum
Unit 5: Rotation
Unit 6: Oscillations
Unit 7: Gravitation
Studying for another AP Exam?
Check out our other AP study guides
Tags
 Knowt
Knowt