Chapter 6 - Set theory
0.0(0)
Studied by 0 people0.0(0)
Call Kai
Learn
Practice Test
Spaced Repetition
Match
Flashcards
Knowt PlayCard Sorting
1/12
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
13 Terms
1
New cards
A formal universal conditional statement
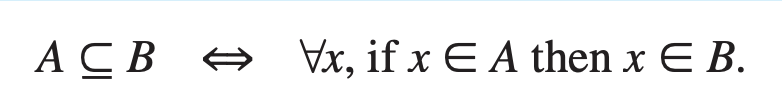
2
New cards
The negation of a universal conditional statement
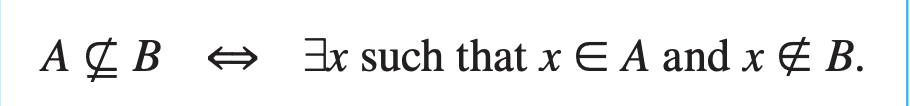
3
New cards
Proper subset
4
New cards
Element Argument: The basic method for proving that one set is a subset of another
1. Suppose that x is a particular but arbitrarily chosen element of X. 2. Show that x is an element of Y.
5
New cards
A = B
A ⊆ B and B ⊆ A.
6
New cards
The union of A and B (A ∪ B)
The set of all elements that are in at least one of A or B.
7
New cards
The intersection of A and B (A ∩ B)
The set of all elements that are common to both A and B.
8
New cards
The difference of B minus A (or relative complement of A in B), (B - A)
The set of all elements that are in B and not A.
9
New cards
The complement of A (Ac)
The set of all elements in U that are not in A.
10
New cards
Two sets are called disjoint off
They have no elements in common (A ∩ B
11
New cards
Sets A1, A2, A3, ... are mutually disjoint (or pairwise disjoint or nonoverlapping) iff
No two sets Ai and Aj with distinct subscripts have any elements in common (Ai ∩ Aj
12
New cards
A partition of set A
A collection of non-empty, mutually disjoint subsets (called blocks or parts) whose union is the original set.
13
New cards
Given a set A, the power set of A, denoted 𝒫(A), is the set of?
All subsets of A.
Note 
Flashcards (52)