LOGIKA IN ARGUMENTACIJA 1 IZPIT

2024/25

Osnovna logična načela

logika je znanost o oblikah racionalnega jezika

1. Načelo identitete (A = A)
Vsaka stvar je v istem času, prostoru, svetu itd. identična sama sebi. 
Če se vsebina pojma v kontekstu spreminja, je treba to izrecno navesti.
Variabla = simbol, ki nadomešča določeno kategorijo jezikovnih izrazov

2. Načelo neprotislovnosti (ni res, da A = ¬A)
Ni možno, da sta stavek in njegova negacija sočasno resnična

3. Načelo izključitve tretjega
Nujno je, da je resničen stavek ali njegova negacija

4. Načelo zadostnega razloga
Vsak resničen stavek mora imeti svoj zadosten razlog, ki utemelji zakaj je resničen. 

Kaj je argument v logiki in kako ga prepoznamo - primeri

Argument je niz trditev (stavkov, propozicij), ki ga
sestavljajo premise in sklep tako, da premise podpirajo
sklep.

Prepoznamo ga tako, da poiščemo sklepe in premise, te pa zaznamujejo naslednje besede;
S: torej..., zato..., od tod sledi... itd.
P: kajti..., ker..., kot kaže... itd.

Deduktivni in induktivni argumenti - razlike

1. Definicija:
De: Logično konkluzivna podpora sklepov (če so premise resnične je obvezno tudi sklep resničen)
In: Premise vplivajo na argumentovo "induktivno moč" (tudi če so premise resnične je sklep lahko neresničen)

2. Razlike:
De: Sklep vedno sledi iz premis, zaradi tega je močnejši deduktivni argument
In: Premise dokazujejo le z neko verjetnostjo podpirajo sklep

Sestavni deli argumentov in osnovni logični vezniki (zanikanje, konjunkcija, disjunkcija, pogojnik)

1. Zanikanje/negacija (ne P, ¬P)
Z zanikanjem dobimo nasprotno resničnostno vrednost

2. Konjunkcija (P in Q, P ∧ Q)
Sestavljena trditev, v kateri trdimo hkratno resničnost dveh trditev

3. Disjunkcija (P ali Q, P ∨ Q)
Sestavljena trditev, v kateri trdimo, da je resnična vsaj ena od dveh trditev (lahko tudi obe, ne pa nobena)

4. Implikacija (če P, potem Q, P ⊃ Q)
Ko zatrdimo pogojnik ne zatrdimo resnice samo prvega člena, ali samo drugega člena, ampak resnico celotnega pogojnika. Ta je resničen v vseh primerih razen ko je prvi resničen, drugi pa ne. 

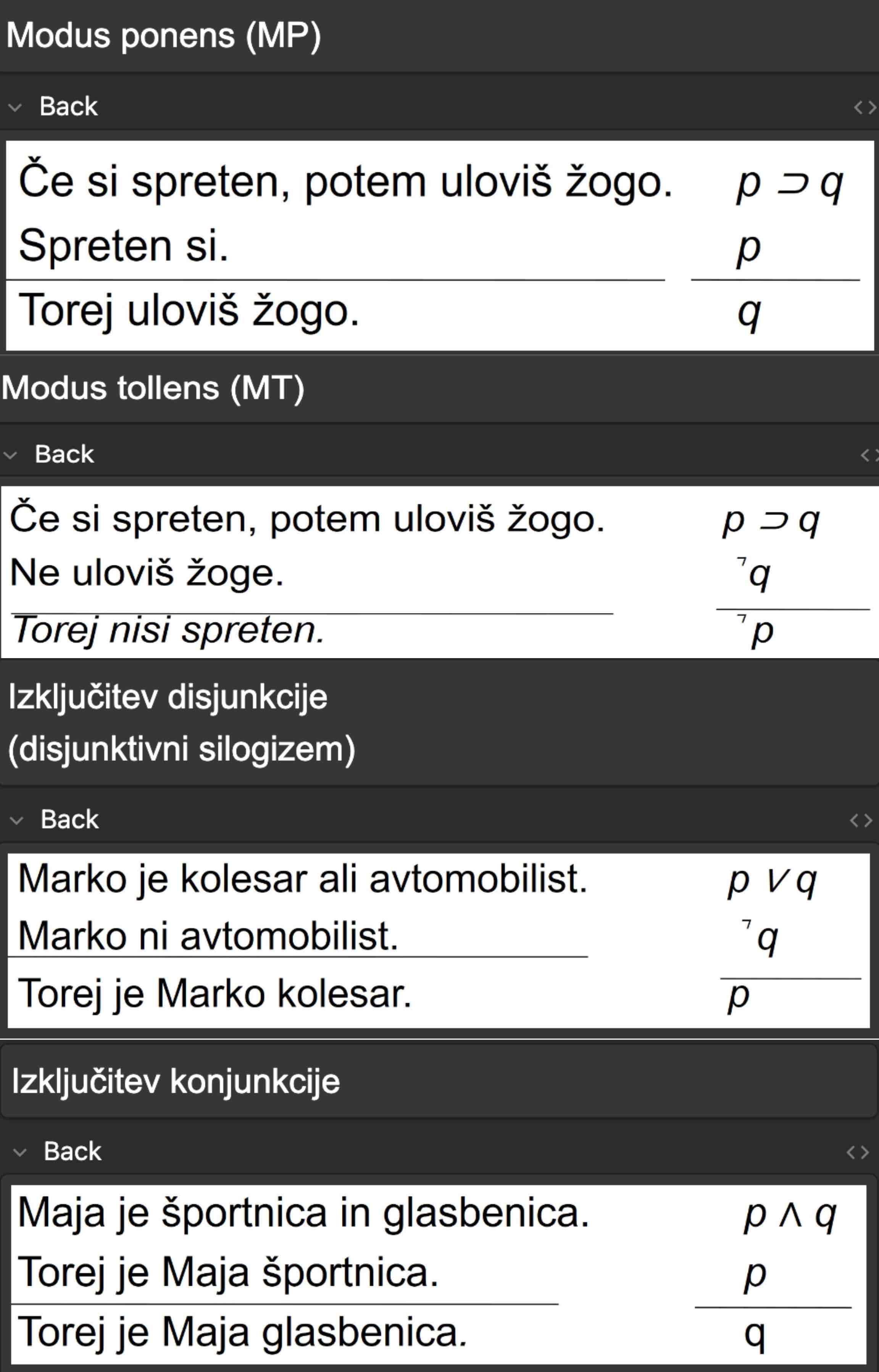
Definicija veljavnega/zdravega/dobrega argumenta, primeri veljavnih deduktivnih argumentativnih shem (modus ponens, modus tollens, ...)

Veljaven: Ni mogoče, da so vse premise resnične, sklep pa neresničen.
Zdrav: Veljaven in vse premise so resnične
Dober: Premise so relavantne sklepu, ni jezikonih nejasnosti, argumentacija ni krožna

*Dokazovanje veljavnosti argumentov (primerjalne tabele, semantična drevesa)

1. prevajanje v jezik stavčne logike: razberemo elementarne stavke, jih spremenimo v stavčne variable npr. p,q, poiščemo veznike in jih prevedemo, postavimo oklepaje

2. tabeliranje sestavljenih stavkov: iščemo tavtologijo, kontradikcijo ali kontingenten stavek

3. primerjalne resničnostne tabele: izpišemo posamične varaible, premise in sklep→ iščemo vrstico, kjer so vse premise in sklep hkrati veljavne

4. semantična drevesa: z razstavljanjem iščemo protislovja med stavki- če je protislovje, potem se veja zapre → če ni več nobene veje je arument nekonsistenten in ne velja

Formalne napake - primeri

Formalne napake so posledica kršenja pravil sklepanja ali pa sledijo »pravilu«, ki je sicer podobno veljavni shemi sklepanja, a je neveljavno- gre za sofizem

deduktivni argument katerga sklep ne sledi iz premis in ne velja

Sklepanje na način reductio ad absurdum (zvajanje na protislovje)

Zmote relevance

Premise, ki naj bi podpirale sklep, niso z njim v relevantni zvezi.
1. Argument proti človeku (ad hominem) - spodbijanje verodostojnosti, ki podaja argumente, namesto argumentov samih
2. Zmota iz nevednosti - ker nekaj ni dokazano, sklepamo, da je resnična nasprotna trditev
3. Zmota sklicevanja na čustva - igranje na čustva namesto podanja argumentov
4. Zmota sklicevanja na splošno mnenje - zanašanje na splošno mnenje namesto razum
5. Napačno sklicevanje na avtoriteto - trditev sprejmemo kot resnično samo zato, ker tako pravi oseba, čeprav ta oseba ni strokovnjak z dotičnega področja

6.zmota zastrupljenega vodnjaka- nasprotnika že naprej diskreditiramo

7.slamnati mož- napadamo karikaturo stališča

8.sklicevanje na moč

Zmote zaradi jezikovnih dvoumnosti in zmote krožnega sklepanja

1. Jezikovna dvoumnost:
Nastopi takrat, kadar zlorabimo nejasen pomen besede, sklopa besed (fraze) ali stavka.
-Semantično dvoumje (beseda je lahko interpretirana na več načinov)
-sintaktično dvoumje (zaradi slovnične konstrukcije)
2. Krožno sklepanje:
Nastopi takrat, kadar že vnaprej predpostavimo resničnost tistega, kar šele želimo dokazati. Sklep argumenta je že vsebovan v premisah ali pa je v njih predpostavljen.

3.obteženo vprašanje- ne moreš nasprotovati, brez da bi se strinjal z podtaknjeno trditvijo

Zmote nepotrjenih predpostavk

Argumenti temeljijo na vprašljivih načelih (predpostavkah), ki niso splošno veljavna.

1. Zmota kontinuuma (sorites) - predpostavlja, da so majhne spremembe vedno nepomembne
2. Zmota kompozicije - domneva, da ima celota vedno iste lastnosti kot posamezni deli
3. Zmota delitve - domneva, da lahko lastnosti, ki jih ima celota, pripišemo tudi njenim posameznim delom
4. Zmota napačnih alternativ - premajhno število alternativ

5.spolzka strmina- da majhna sprememba vodi do drastične spremembe

Značilnosti induktivnih argumentov; induktivno posploševanje - primeri

-premise z dokajšnjo stopnjo podpirajo sklep
-možno, da so premise resnične in sklep neresničen
-množica premis je nezaključena
-ni monotona (za razliko od dedukcije)

Posploševanje:
1. Induktivna generalizacija (verjetnostno sklepanje od premis, ki izražajo posamezne ali posebne izkustvene trditve k sklepom, ki izražajo univerzalne zakonitosti)
2. Statistišna generalizacija (reprezentativni vzorec je enak celotni "populaciji")
3. Humovska indukcija (Če za vse do sedaj znane elemente poljubne množice velja neka lastnost, potem ta lastnost velja za čisto vse elemente te množice)

4.enostavna indukcija- iz znanega sklepamo na naslednje

Abdukcija - sklepanje na najboljšo možno razlago - *primeri

Iz dostopnih empiričnih dokazov sklepamo na najboljše pojasnilo za opaženo dejstvo ali pojav (predlagamo najbolj verjetno razlagalno hipotezo)
Splošna shema abdukcije:
-Če drži hipoteza H, potem nastop dejstvo D.
-Nastopi dejstvo D
>Zelo verjetno drži hipoteza H

sherlock holmes

Argumenti po analogiji - kriteriji, primer*

Iz podobnosti dveh množic v eni ali več lastnostih sklepamo na podobnost tudi v drugih lastnostih.
Verjetnost je odvisna od:
-števila skupnih lastnosti
-bistvenosti teh lastnosti
-relevantnosti med znanimi in sklepanimi podobnosti

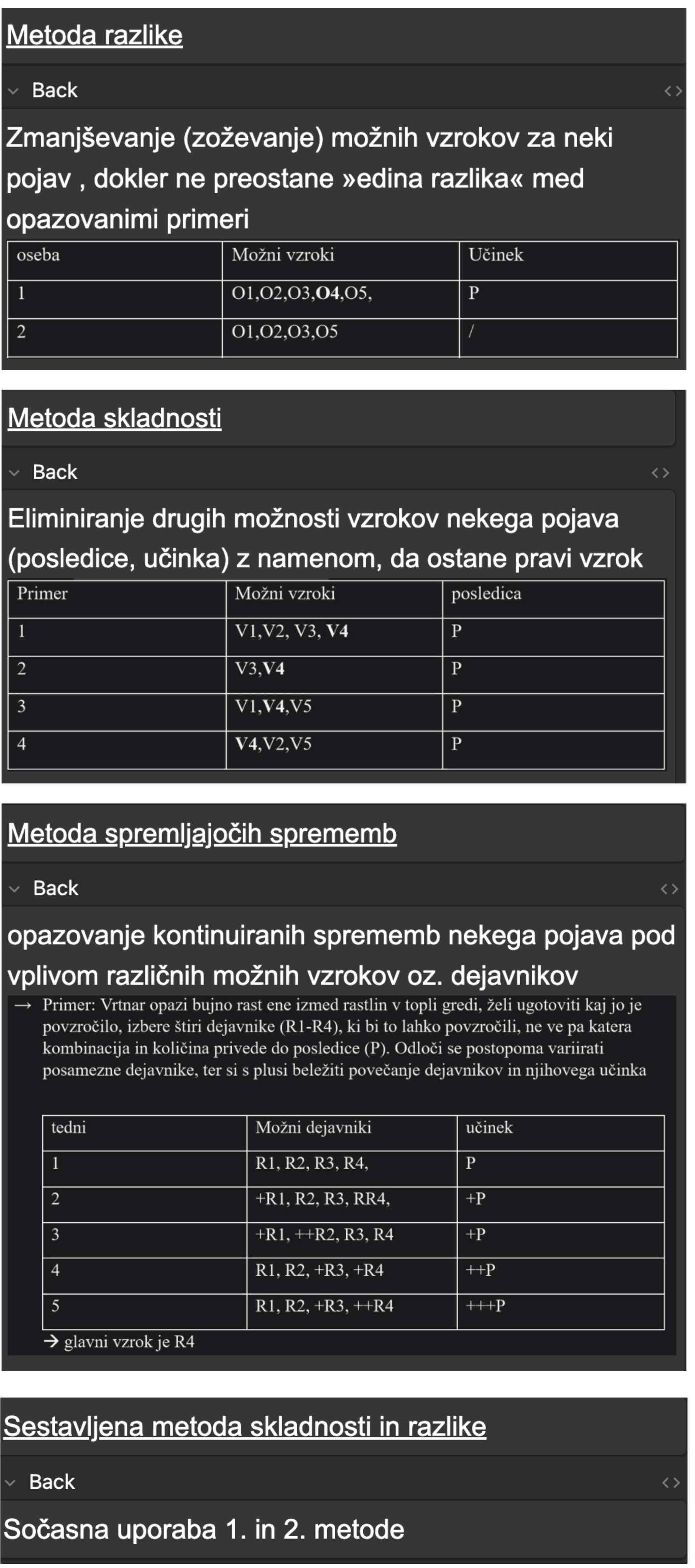
Millove induktivne metode - *primeri

1. Metoda razlike- zmanjševanje vzrokov, dokler ne ostane razlika med pogoji za pojav in ne-pojav
2. Metoda skladnosti- eliminiranje vzrokov, dokler ne pridemo do vzroka skupnega vsem pojavom
3. Metoda spreminjajočih sprememb- opazovanje kontinuiranih sprememb in kako dejavniki tudi vplivajo na ostale dejavnike
4. Sestavljena metoda skladnosti in razlike- išče kar je skupno in kar je različno→ iskanje nujnega in zadostnega vzroka

Zmote induktivnega sklepanja - *primeri

1. Zmota prehitre posplošitve
je napaka, ki jo zagrešimo pri induktivni generalizaciji, ko sklepamo na trditev o celotnem razredu stvari na osnovi (neustreznega) poznavanja nekaterih članov razreda ali pri statistični generalizaciji, kjer vzamemo nereprezentativen vzorec ali uporabimo neustrezno tehniko vzorčenja
2. Zmota pri sklepanju po analogiji
Kadar sta pri sklepanju po analogiji stopnja in relevanca podobnosti precej majhni.
3. Hazarderjeva zmota
Temelji na neupravičeni postavki, da se bo vrednost dogodka, ki sledi nizu slučajnih dogodkov, ki so vsi imeli določeno vrednost, gotovo spremenila.
4. Zmota napačnega vzroka
Korelacija je obravnavana kot vzrok. 

*Stavčna (propozicijska) logika (»P« sistem)

propopzicije nosijo resničnostne vrednosti- 1 ali 0

stavek izraža propozicijo, več istih stavkov lahko izraža isto propozicijo

resničnostne funkcije: razlikovanje med atomarnimi in molekularnimi stavki

molekularni stavek je resničnostna fukcija ko je njegova resničnostna vrednost odvisna od resničnostne vrednosti atomarnih stavkov

konstrukcija sistema: -sintaksa: varible, vezniki, stavčni operatorji, oklepaji

-semantična matrica P-sistema: 16 različnih kombinacij resničnostnih vrednosti iz katere izpeljemo vse stavčne veznike

Tavtologija, kontradikcija, kontingentna formula

1. Tavtologija
Je resničnostna funkcija, ki je vselej resnična, ne glede na resničnost ali neresničnost njenih argumentov (logično resničen stavek)
2. Kontradikcija
Je negacija tavtologije: je resničnostna funkcija, ki je vselej neresnična, ne glede na resničnost ali neresničnost njenih argumentov (logično neresničen stavek)
3. Kontingentna formula
Niso ne niti logično resnični niti logično neresnični

Prevajanje logičnih veznikov; De Morganov zakon

1. ¬p ∨ ¬q ↔ ¬(p∧q)(negacija konjunkcije = disjunkciji negacij)
2. ¬(¬p ∨ ¬q) ↔ p∧q        
3. p∨q ↔ ¬(¬p ∧ ¬q)     
4. ¬p ∧ ¬q ↔ ¬(p∨q) (negacija disjunkcije = konjinkciji negacij)

Naravna dedukcija - pravila

Vsebina in obseg pojmov, definicije in pravila definiranja v aristotelski logikI

1. Osnovni elementi: pojmi/termini
Vsebino tvori niz bistvenih določil pojma.
Obseg je zamejen z množico vseh posameznih primerkov, ki imajo ista bistvena določila.
2. Definicija (opredelitev) določa vsebino pojma in jo sestavljata: “tisto, kar naj bo definirano” (definiendum) in “tisto, kar definira” (definiens)
Definiens se naprej deli na najbližji rod in vrstno razliko.

Stavki v silogistični (Aristotelski) logiki, Eulerjevi diagrami

1. Stavek - govor, s katerim se nekaj o nečem potrjuje ali odreka
2. Tisto, kar se potrjuje ali odreka, je v aristotelski logiki predikat stavka
3. Tisto, o čemer se nekaj potrjuje ali odreka je subjekt stavka
4. Subjekt in predikat sta v stavku povezana s kopulo

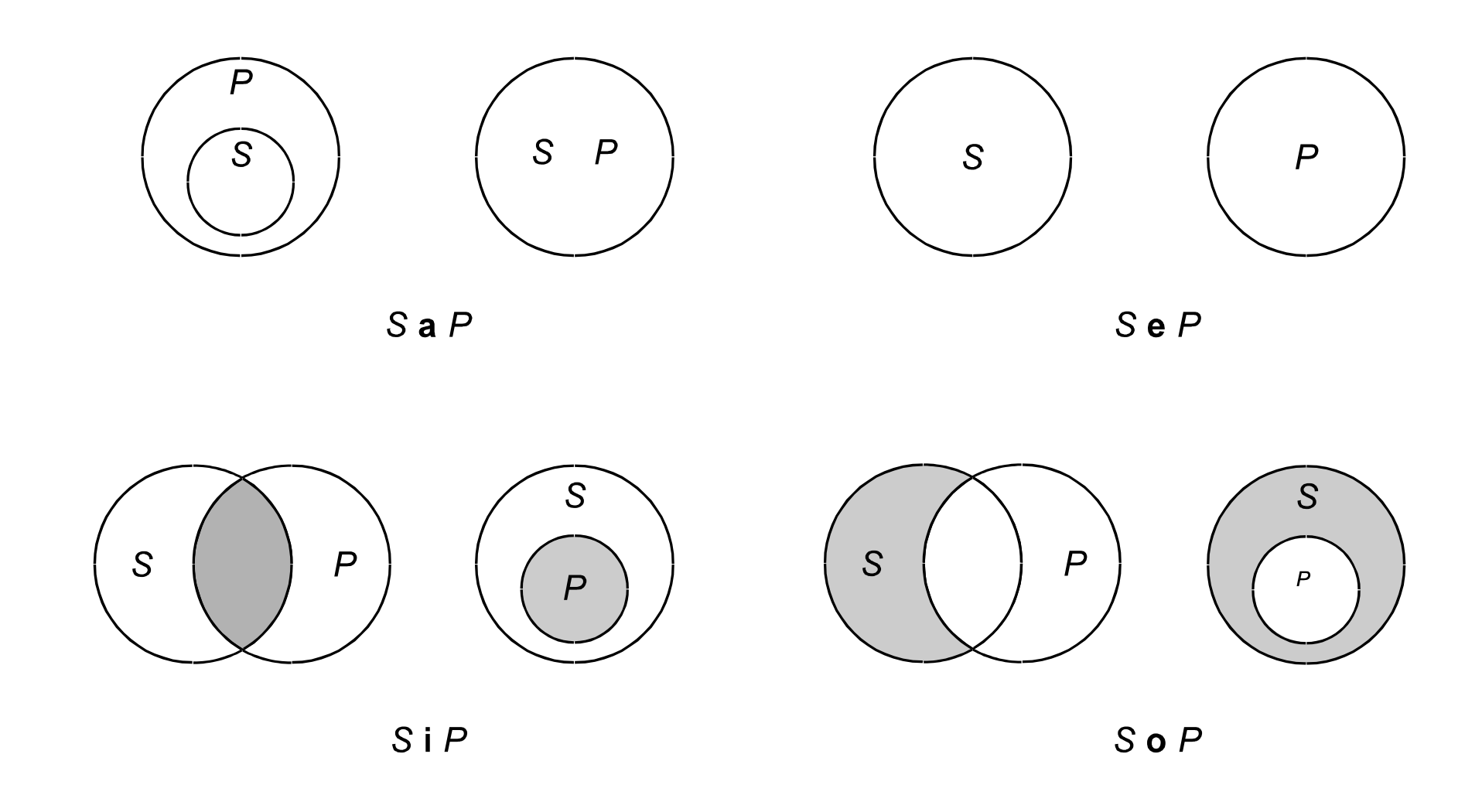
Enostavna sklepanja v silogistični logiki in logični kvadrat

1. Obrat (konverzija)
Iz S a P sledi P i S
Iz S e P sledi P e S
Iz S i P sledi P i S
2. Premena (ekvipolenca)
Iz S a P sledi S e ne-P
Iz S e P sledi S a ne-P
Iz S i P sledi S o ne-P
Iz S o P sledi S i ne-P
3. Preobrat (kontrapozicija)
Iz S a P sledi ne-P e S
Iz S e P sledi ne-P i S
Iz S o P sledi ne-P i S

Aristotelovi silogizmi

*Predikati in stavčne funkcije (osnove Q-sistema)

Q sistem razrširi stavčno logiko- omogoča silogositčno sklepanje z relacijami: vsi so, vsi niso, nekateri izmed so/niso

predikati: -enomestni predikat se nanaša na 1 sam subjekt

Sm S-smrten=preidkat m-Marko

lahko izražajo lastnost individua al množice

stavčne funkcije: Sx→ inidviduum posplošimo na poljubnega posameznika/ spremenljivko

Stavčna funkcija - x je smrten => Stavek - Marko je smrten

Univerzalni in eksistenčni kvantifikator

Univerzalni kvantifikator (∀x) "za vsak x velja..."
Eksistenčni kvantifikator (∃x) "obstaja vsaj en x, za katerega velja..."

Logika relacij, lastnosti relacij, ekvivalenčne relacije

Relacija: predikat stopnje n>1
Lastnosti:
1. Refleksivnost
2. Tranzitivnost
3. Simetričnost
Ekvivalenčne relacije: ustrezajo vsem trem pogojem

*Aksiomski sistemi - Russellov aksiomski sistem

aksiom = temeljna resnica

aksiomatika- urejamo lahko množico tez nekega poročja iz manjšega števila izhodniščnih tez/ aksiomov

sistematika, logika, Evklid- geometrija- askiom o vzporednicah

sistemi imajo sintaktična pravila, definicije, aksiome, izreke

Russell: iz negacije in disjunkcije definira konjunkcijo, implikacijo, ekvivalenco..

aksiomi so simplifikacija, adicija, komutativnost, asociativnost, tranzitivnost- morajo biti konsistentni, semantično popolni, sintaktično popolni, medsebojno neodvisni

teoremov je toliko kolikor je tavtologij

Kaj so logični paradoksi (Russellov, »lažnivec«, sorites – kup)

Protisloven sklep iz premis, ki jih smatramo za resnične, do katerega pridemo z logično izpeljavo, ki je na videz pravilna. 

1. Russellov paradoks: 
Množica N je množica vseh normalnih množic.
-Če je normalna, vsebuje sebe, a potem ni več normalna
-Če ni normalna, potem vsebuje sebe, torej vsebuje množico ki ni normalna

2. Lažnivec:
Epimenid ix Krete: "Vsi Krečani vedno lažejo"

3. Sorites - kup:
Imamo kup peska, ki mu zrno po zrno odstranjujemo pesek. Po keterem zrnu neha kup biti kup?

*Zenonovi paradoksi

Zenon iz Elee, 5. stol. pr. n. št. učenec Parmenida (Eno- mnoštvo in gibanje so iluzije čutov)

1. ahil in želva- ahil želve ne more ujeti, ker ma priority move (pokemon) in a ves hsr turn based combat ampak tle je turn based speed competition in želva bo mela prednost ne glede na to kok ms in speed stats builda ahil

2. puščica- ko iztreliš puščico, ko leti v vsakem zavzema prostor, ki je enak njeni dolžini- torej se ne premika, ker je trenutek kot enota nedeljiv- torej puščica v trenutku miruje

3. argument proti mnoštvu: reductio ad absurdum argument, da obstoj mnoštva stvari vodi v protislovje- nedeljivost delcev pomeni, da zasedajo neomejen prostor ali pa nobenega prostora (noben argument ni zdrav)