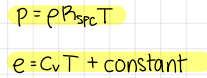1.4. Fundamental equations

Definition of material volume v(t)

it’s a control volume evolving in time in such a way to be made up by the same fluid particles moving with the fluid (v(t))

Physical property of fluid particle

continuously deformable and of arbitrary size

Mathematical properties of fluid particles

the evolution of each fluid particle within the material volume can be described by a continuous bi-injective function (so that the volume v(t) at any time t can be tracked back to the volume v*=v(t=0))

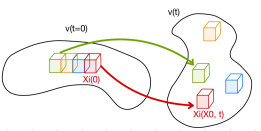
what is x_i equal to? (material volume)

x_i=f_i(xi(0),t)

what is f_i? (material volume)

bi-injective and continuous

the material volume v(t) is made out of…

the same moving particles moving with the fluid, it will always contain the same fluid particles

What is the Reynolds transport theorem useful for?

to calculate the time variation of an integral quantity within a material volume

The two terms on the right hand side of the following identify… (Reynolds transport theorem)

two contributions to the total variation:

• the variation in time due to an intrinsic non stationarety of G

• the variation due to the changes of the integration volume

Because of the bi-injectivity of the function describing the time-evolution of the material volume… (Reynolds transport theorem)

the balance can be expressed in terms of the initial volume v*, the results can be generalized to any type of fixed volume

Developing of right hand side (Reynolds transport theorem)

formulas

Conservation laws applicable to a material volume

• Conservation of mass

• Conservation of momentum (general and specialized for Newtonian fluid)

• Conservation of energy (total, kinetic, internal)

Statement of conservation of mass

the mass of any arbitrary material volume remains constant in time

Developing of equation of conservation of mass

formulas

(conservation of mass) if v(t) is an arbitrary material volume, and the system is continuous:

Localization lemma

formulas

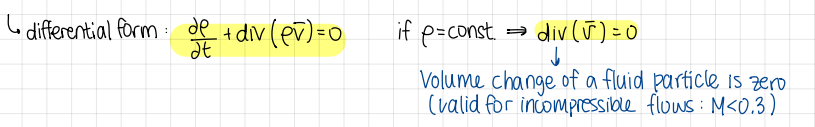
Statement of conservation of momentum (or Newton’s 2nd law)

the rate of change of momentum of any arbitrary material volume is equal to the sum of the external forces applied on the volume

Formula for rigid bodies (conservation of momentum)

formula

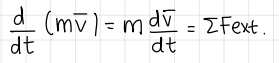
Formula for fluid bodies (conservation of momentum)

formula

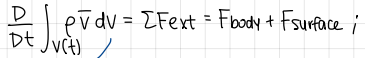
Left hand side of conservation of momentum

formulas

Right hand side of conservation of momentum

formulas

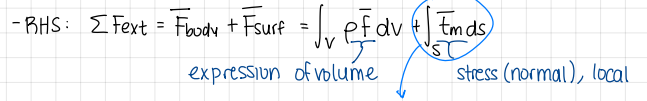
The goal of the stress term in the RHS of conservation of momentum

the goal is to transform the surface volume into a volume integral and represent t_n with the minimum number of uknowns independent of n (Cauchy theorem)

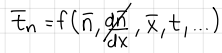
The stress tensor: cauchy theorems: formulas

formulas

(stress tensor: cauchy theorem) If the limit of I (size of thetraedron) goes to zero…

the terms that depend on mass vanish more rapidly than the terms depending on the surface

so the only way to respect the balance of momentum is for the surface forces to be identically zero

The stress tensor: cauchy theorems: more formulas

formulas

Stress tensor

tensor

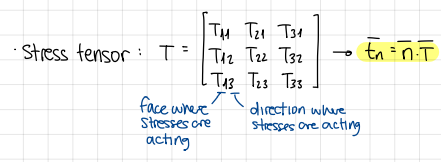
What do the components of the stress tensor T represent?

the components of the stresses acting on three orthogonal planes intersecting with surface dA (ex. the ones defined by the system of reference)

The components of the stress tensor T are…

independent on n, but only on the choice of the reference surfaces

for example, T11 is the component of t1 acting normal to the surface A1, while

T12 is the component tangent to A1 in the direction 2, etc.

2nd Cauchy theorem (stress tensor)

Tij=Tji

By similar reasoning (to 2nd Cauchy theorem) applied to the conservation of angular momentum it can be shown that…

the stress tensor is symmetric

Mechanical pressure formula

formula

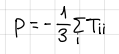
Formula for stress tensor for a fluid at rest (mechanical pressure)

formula

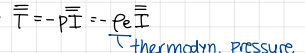
Formula for stress tensor in general (mechanical pressure)

formula

More development of right hand side of conservation of momentum, formulas

formulas

Expanded Localization lemma, formula

formula

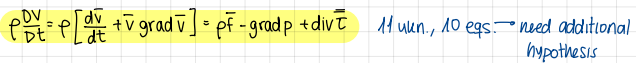
Why need closure hypothesis?

Problem: 4 equations and 11 uknowns → need to introduce some hypotheses

Characteristics of closure hypothesis

• The derived equation is valid for any continuously deformable medium

• To reduce the number of uknowns we need to make some hypothesis on the type of medium, and in particular on the relationship between the stresses and the deformation rates

Assumptions of closue hypothesis

1. T is a continuous function of E only

   1. gradv=E+omega

2. when E=0 → the fluid will be at rest → Ts=-p_e*I

3. f(E) is independent of position

4. f(sigma) is independent of orientation

Viscosity in closue hypothesis: formula

formula

lambda and mu: first and second viscosity coefficents

formulas of i_ij in closure hypothesis

formulas

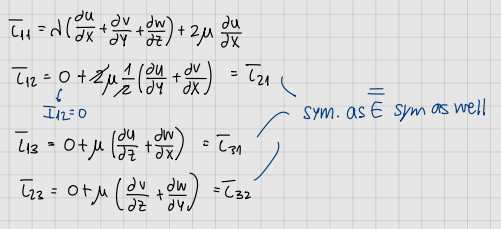
formula of E (closure hypothesis)

formula

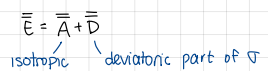
formula of A (closure hypothesis)

formula

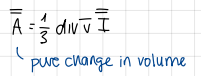
formula of viscosity (closure hypothesis)

formula

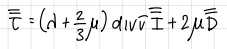
formula of stress tensor T (closure hypothesis)

formula

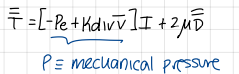
formula of kappa (closure hypothesis)

formula

(closure hypothesis) P=P_e if:

• v=0 → P=(-Pe+kappa*div v)

• div v=0 (incompressible flow)

• kappa=0 → lambda=-2/3*mu (Stokes hypothesis)

• kappa*div v « Pe

Developmend and general equation for momentum balance

formulas

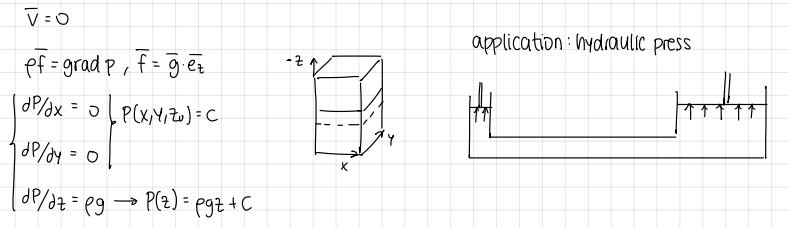
Pascal principle definition

in an incompressible fluid, any change of pressure is instantaneously transmitted to any other point of the fluid

formulas of hydrostatics

formulas

Archimedes principle

a body wholly or partially immersed in a fluid experiences an upward buoyant force equal in magnitucde to the weight of the fluid displaced by the body

how can the Archimedes principle be derived?

from the momentum quation in integral form by noting that a fluid volume at rest is subjected to the following condition:

formula

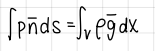
physical explanation of Archimedes principle

for a fluid at rest , the resultant of the hydrostatic pressure acting on any surfaces is equal to the weight of the volume of fluid that it encloses·Therefore, if we replace the mass of fluid with another element it will be subjected to the same pressure forces , whose resultant is a net force in the direction opposite ofthe body force (i .e. upward for gravity!) equal in magnitude to the weight of the displaced volume!

formula

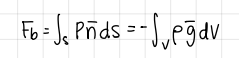
application of Archimedes principle

ships, balloons, etc.

statement of conservation of energy

the variation in time ofthe total energy (i .e.internal and kinetics) of any arbitrary material volume is equal to the sum of work per unit time (power) done by the external forces and the neat heatflux transmitted to the volume

principle of conservation of energy (formulas)

formulas

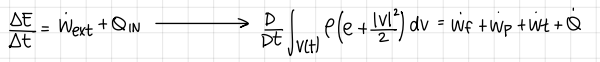
formula and units of work per unit time done by the body forces (conservation of energy)

formula and units

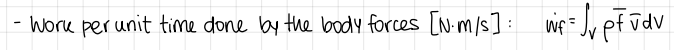
formula and units of work per unit time done by pressure (conservation of energy)

formula and units

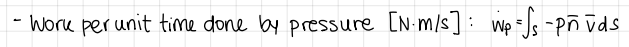
formula and units of work per unit time done by viscous stresses (conservation of energy)

formula and units

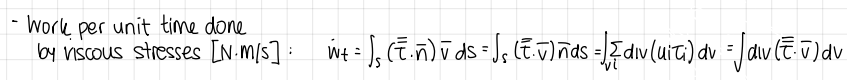
formula and units of heat transferred per unit time through the volume surface

formula and units

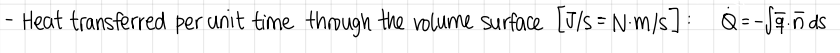
how do you get the differential form of the total energy balance?

by applying Reynold's transport theorem to the right hand side, Divergence theorem and localization Lemma

formula of the differential form of total energy balance

formula

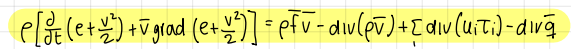
what can we do in order to isolate the contribution of the kinetic and integral energy to the total energy?

we can derive a balance equation for the kinetic energy from the momentum equation

formula of kinetic energy

formula

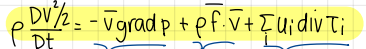
what is this term of the formula of kinetic energy (1/3)

• contribution to the kinetic energy of the pressure gradient

• positive or negative depending on the sign of the pressure gradient

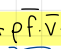
what is this term of the formula of kinetic energy (2/3)

• contribution to the kinetic energy due to volume force (ex. buoyancy)

• positive or negative in the direction of the body force

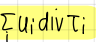
what is this term of the formula of kinetic energy (3/3)

contribution to the kinetic energy due to viscous action

development of internal energy equation

formulas

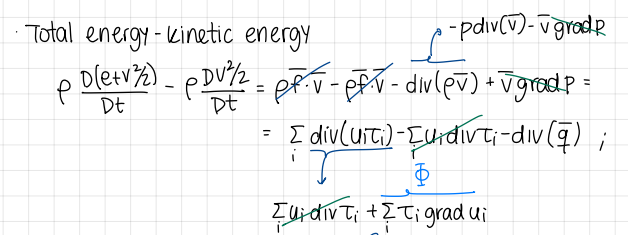
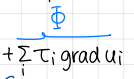
what does this term of the internal energy equation do?

• it increases the internal energy

• represents the work done per unit time by viscous stresses

write the internal energy equation

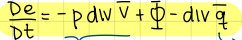
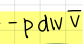
what does this term of the internal energy equation mean? (1/3)

reversible due to compression or expansion

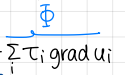
what does this term of the internal energy equation mean? (2/3)

dissipation term

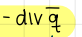
what does this term of the internal energy equation mean? (3/3)

external heat source

write the entropy balance equation and it’s condition

equation

condition → entropy must not decrease for closed systems

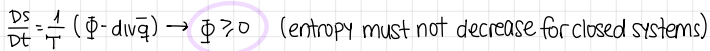
definition of entropy

• it’s the measure of the molecular disorder of our system

• it can only increase or remain constant

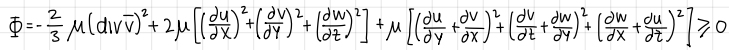
what is this expression?

entropy balance for newtonian fluids

why does dissipation happen?

due to the work done by the viscous stresses to deform a fluid particle

what does dissipation represent?

represents an irreversible form of energy transfer towards the internal energy (ex. increase fluid temperature)

more constitutive equations?

• state law for thermodynamic pressure

• heat conduction (radiation to be included if present)

• state law for pressure

• state laws for ideal gas (2)

state law for thermodynamic pressure (formula)

formula

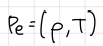
heat conduction (radiation to be included if present) (formula)

formula

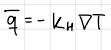
state law for pressure (formula)

formula

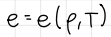
state laws for ideal gas (2 formulas)

formulas