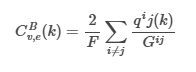9: Community Analysis in Complex Networks

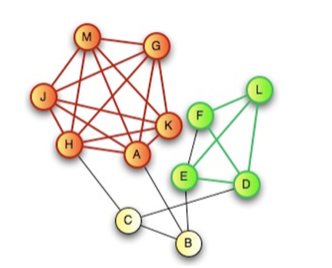
Community

A subset of nodes within a graph such that the connections between these nodes are denser than the connections with the rest of the network.

Strong Community

Every node in the community has more connections internally to the community than externally.

Weak Community

Every node in the community has more connections externally than internally.

Strong Community Formula

For all vertices vⁱ in a subgraph V_c, degree_vc(vⁱ) > degree_{not vc}(vⁱ)

Weak Community Formula

The sum of all vertices’ degrees in the subgraph compared to the sum of all vertices’ degrees in the subgraph compared to outside the subgraph.

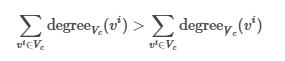
Length of a chain

The number of edges it contains.

Distance between two vertices

The length of the shortest chain between those vertices.

Graph diameter

The longest distance between any two vertices.

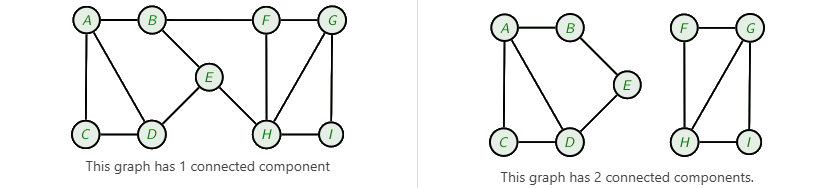
Connected component (of an undirected graph)

A subgraph in which any two vertices of the subgraph are connected to each other that is connected to no additional vertices of the subgraph.

• A function used to count connected components in a graph is ω(G)

Connected Graph Requirements

• There is only 1 connected component

• Or every partition of its vertex set into two non-empty sets V_X and V_Y there is at least one edge with one end in V_X and its other end in V_Y

Free Graph

A graph with no edges

Complete Undirected Graph

Every party of different vertices are connected.

Complete Graph Size

With order |V| = n, it is always |E| = (n(n - 1))/2

Trajectory

A directed path

Weakly Connected Directed Graph

There is a path between any pair of nodes where each node is different.

• All strongly directed graphs are also weakly connected.

Strongly Connected Directed Graph

There is a directed path between any pair of different nodes, i.e. where there is a path between every pair of nodes, even when considering the direction of edges.

Depth-First Search

Searching children before siblings.

Breadth-First Search

Searching siblings before children.

Removing a Vertex

Remove the vertex and all of the edges connected to it.

Removing a Vertex (Formally)

In a graph G = (V, E), the graph H = G - v = (v^H, e^H) is the subgraph resulting from removing v in V from G, v^H = V - {v} and all incident edges, for all edges e in E that aren’t v but are in e^H.

Removing an Edge

Only remove the edge without any further modifications.

Bridge

An edge of a graph whose deletion increases the number of connected components within the graph.

• ω(G \ e) > ω(G)

Cut Vertex (Articulation Point)

A vertex that when removed increases the number of connected components within the graph.

• ω(G \ v) > ω(G)

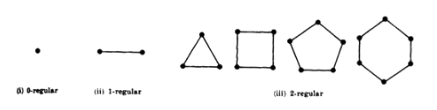
K-Regular Graph

A graph where all of its vertices have the same degree.

Bipartite Graph

The vertices of the graph can be partitioned into two subsets, such that all edges connect to a vertex of V₁ and a vertex of V₂.

Set Partitioning

Splitting a set into subsets, such as the union of all subsets is the same as the whole set.

Bipartite Graph Formally

For all edges (e = (vⁱ, v^j) in E), vⁱ is in V₁ and v^j is in V₂

Complete Bipartite Graph

Every vertex in V₁ is connected to every vertex in V₂.

Clique

A subset of a graph that is complete and minimal.

Tree

A graph where every pair of vertices is joint by a single chain.

• It is simple, acyclic and connected.

Internal Tree Vertex

A vertex that has a degree of 2 or more.

Leaf Node

A vertex with a degree of 1.

Modularity

The measure of the structure of a graph, measuring the strength of division of the graph into modules (cliques, clusters, communities).

Calculating Modularity (Simple)

Assume we want to divide a graph G into k subgraphs.

• Define a symmetric matrix M_{k x k} = {m_ij} with elements m_ij that are the fraction of all edges in the network that link vertices in the subgraph V_i with vertices in the subgraph V_j

• The row and column sums m_i = Sum of all m_ij for each j represent the fraction of edges that connect to vertices in subgraph V_i

• In a graph where edges fall between vertices without regarding the division, we would see m_ij = m_im_j

Modularity (Formula)

Where:

• M_{k x k} = {m_ij} where M is a symmetric matrix and m_ij are the elements that are the fraction of all edges in the network that link vertices in the subgraph V_i with vertices in the subgraph V_j.

• ||M|| is the sum of elements in the matrix.

• Trace(M) is the sum of the main diagonal element

  • Represents the fraction of edges in the graph that connect to vertices in the same subgraph

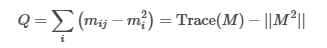
Newman-Girvan Modularity Formula

Where:

• a_ij is the weight of the edge between vⁱ and v^j

• kⁱ = the sum of weights of the edges attached to the vertex vⁱ

• cⁱ is the community vⁱ is part of

• D(cⁱ, c^j) is 1 if cⁱ = c^j or 0 otherwise

• m = ½ * sum of all elements in the adjacency matrix.

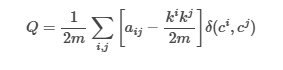
Agglomerative Methods

Start from a free graph and add edges, building the graph from leaves to root.

Divisive Methods

Starting from a complete method, removing edges, in the process building the graph from root to leaves.

Louvain Algorithm

A community detection algorithm that iteratively maximises the difference between the actual number of edges in a community and the expected number of edges in the community.

Girvan-Newman Community Detection

A community detection algorithm based on betweenness - it iteratively computes the centrality for all edges and removes the edge with the greatest centrality, one at a time.

Louvain Algorithm - Phase 1

Builds a partition over the graph, shuffling nodes among neighbouring communities, potentially moving the same node multiple times.

Louvain Algorithm - Phase 2

Build a new graph whose nodes are the communities found in the first place.

• The weights of the links between two community nodes are given by the sum of the weights of the links between nodes in the corresponding two communities.

• Links between the same community lead to self-loops for this community in the new network.

Louvain Algorithm - Pro

Fast and scalable - modularity does not have to be calculated from scratch every time and just the difference can be calculated.

Louvain Algorithm - Con

The output of the algorithm is dependent on the order that nodes are considered in.

Metacommunity

A set of communities that interact with each other.

Girvan-Newman Community Detection - in brief

• For every edge in a graph, calculate the betweenness centrality

• Remove the edge with the highest betweenness centrality

• Calculate the betweenness centrality for every remaining edge

• Repeat steps 2 - 4 until there are no more edges left

Girvan-Newman Community Detection - Betweenness Centrality

Calculated using Freeman’s normalised betweenness centrality for edges.

• q^ij(k) - the number of shortest paths between vⁱ and v^j running through the vertex/edge k (v^k or e^k)

• G^ij is the total number of shortest paths between vertices vⁱ and v^j.

• F is a normalisation factor valued F = (|V| - 1)(|V| - 2) in cases of vertices and F = |V|(|V| - 1) in the case of edges