4.4 Indeterminate Forms and L' Hospitals Rule

What is an Indeterminate Form ?

An expression that arises when evaluating a limit, such as 0/0 or ∞/∞

This is where the result cannot be immediately determined and requires further analysis using techniques like L’ Hopital’s rule.

Why are expressions indeterminate?

These expressions are called "indeterminate" because their value is not fixed and depends on the specific functions involved. For example, the limit of a function that results in  0/0 could be zero, any other finite number, or even infinity. 

We have a limit in the form of

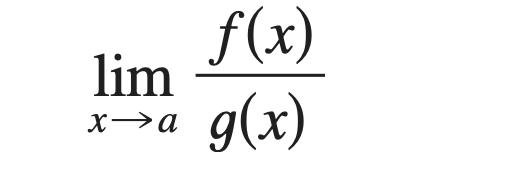
Why is it important to verify the conditions regarding the limits of f and g before using L’ Hospital’s Rule?

1. L’Hôpital’s Rule applies only to indeterminate forms

2. The functions must be differentiable near the point

3. The denominator’s derivative must not be zero

When does an indeterminate Form of type 0/0 occur?

When evaluating a limit and it results in a fraction where both the numerator and denominator approach zero.

When does an indeterminate form of ∞/∞ occur?

When we evaluate a limit where both the numerator and denominator of a fraction grow without bound, approaching infinity.

This situation is common when using L'Hôpital's Rule in calculus, as the result of the limit cannot be determined by simple substitution and could be any value or might not exist. 

RECALL

We saw in Section 2.6 that this type of limit can be evaluated for certain functions, including rational functions, by dividing numerator and denominator by the highest power of x that occurs in the denominator.

L’ Hospitals Rule

L’ Hospitals Rule is a method to use to evaluate limits of indeterminate forms, specifically 0/0 or ∞/∞.

How to use L’H

To use it, take the derivative of the numerator and the derivative of the denominator separately, and then find the limit of the new fraction, which is often easier to solve.

The original limit will have the same value as this new limit, assuming the new limit exists. 

How to apply L’ Hospital’s Rule

Identify an indeterminate form

Differentiate the numerator and denominator

Form a new fraction

Evaluate the new limit

Find the final value

L’Hospital’s Rule

L’Hospital’s Rule says that the limit of a quotient of functions is equal to the

limit of the quotient of their derivatives, provided that the given conditions are satisfied.

Indeterminate Products

Indeterminate products are a type of limit problem in calculus that result in the form of 0×∞ or ∞×.

How to solve indeterminate products? 

To solve them, you must first rewrite the expression as a fraction in the form of 0/0 or ∞∞ so that you can apply L'Hôpital's Rule. 

We can deal with it by writing the product ft as a quotient: 

create a fraction by moving one of the functions to the denominator as its reciprocal

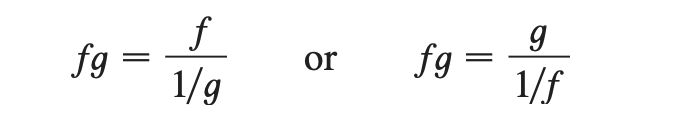
What are indeterminate Differences ?

Indeterminate differences are in form of ∞-∞

How to find indeterminate differences

To find an indeterminate difference, first try to rewrite the expression into an indeterminate quotient (like 0/0 or ∞/∞) by finding a common denominator or factoring.

Once it's in a quotient form, you can then use L Hospital’s Rule or simplify the expression to find the limit. 

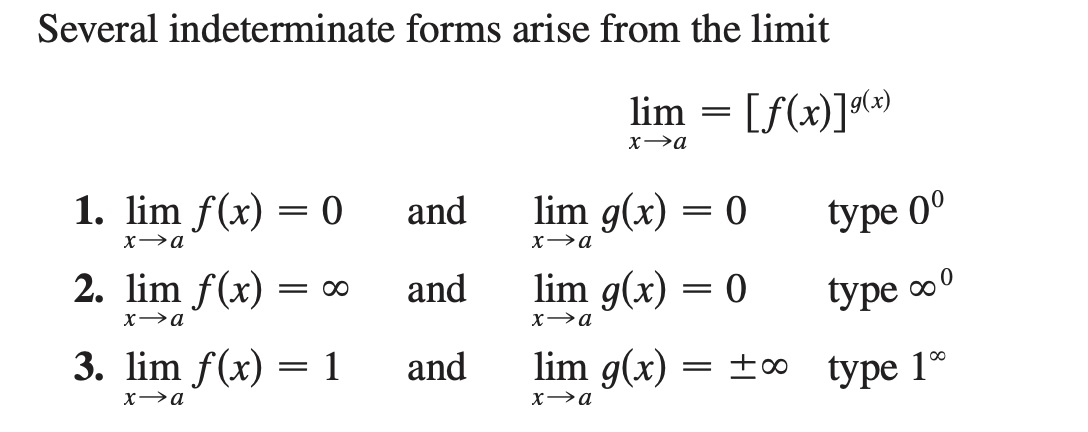
Indeterminate Powers 

The cases of Indeterminate Powers:

Each of these three cases can be treated either by taking the natural logarithm

or by writing the function as an exponential: