Complex Numbers

Cartesian Form

3 + 4i
a+bi

Real Part: 3

Imaginary Part: 4 *Does not include i

Adding/Subtracting/Multiplication Cartesian Form

Deal with the real and imaginary parts separately, imagine they are different variables.

Division Cartesian Form

Multiply the numerator and denominator by the conjugate of the denominator.

Conjugate Cartesian

Denoted by z* and represents the opposite.

If z = a + bi, then z* = a - bi

If z = a-bi, then z* = a + bi

Modulus Cartesian

Denoted by |z|

Represents the distance from the origin

If z = a + bi, then |z| = sqrt(a²+b²)

Argument

The angle that a complex number makes in the diagram

For 1st and 2nd quadrant make sure arg is positive, for 3rd and 4th quadrant argument is negative

Modulus-Argument Polar (Form)

In polar equations r is the distance and we move by the angle. Therefore, r = |z| and θ = arg z.

z = r (cos θ + i sinθ ) or

z = r cis θ

Multiplying (Modulus-Argument)

Moduli are multiplied, and arguments are added.

If z₁ = r₁ cis θ₁ and z₂ = r₂ cis θ₂, then z₁ z₂ = r₁ r₂ cis(θ₁ + θ₂).

Dividing (Modulus-Argument)

Moduli are divided, and arguments are subtracted.

If z₁ = r₁ cis θ₁ and z₂ = r₂ cis θ₂, then z₁ / z₂ = r₁ / r₂ cis(θ₁ - θ₂).

If a number is given in the form z = r (cos θ - i sinθ), this is false

We know that -sinθ = sin (-θ) and cos θ = cos (-θ). Therefore:

z = r (cos θ - isinθ) = r (cos (-θ) + isin(-θ)) = r cis -θ

Converting from Modulus-Argument to Cartesian Form

Just evaluate the cosθ and sinθ.

Euler’s Exponential Form

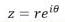
Euler’s Formula

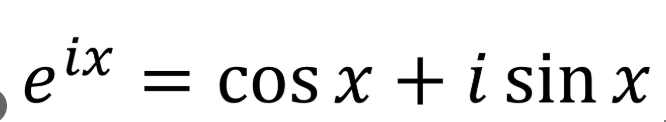
Multiplying/Dividing in Euler’s Form

Same rules as Modulus Argument form.

Writing factors of a quadratic with Complex Roots

De Moivre’s Theorem

Use to raise complex number to a power, this can be also applied to square rooting a complex number (raise to ½ power). It is on the formula sheet.