Chapter 4 Filtering (CP467) Flashcards

Image Processing and Pattern Recognition Chapter 4 Key Terms

Filter

The process of accepting or rejecting certain frequency components

Lowpass Filter

A filter that passes low frequencies

Other terms that “filter” can be called as:

masks, kernels, templates and windows

Spatial Filters

Can alter pixel values based on light intensity variations in a neighborhood. They are more versatile than frequency filters.

What does a spatial filter consist of

-a neighborhood
-a predefined operation

How does filtering work

filtering creates a new pixel:
it replaces the value of a pixel based on the values of neighboring pixels and a defined filter operation (filter operation The process involves applying a mathematical operation like summing, averaging or applying a specific kernel to the pixel values in the neighborhood to generate a new pixel value to replace the center of the pixel neighborhood.

the size of a filter(kernel) is defined and expressed as?

The size is expressed as; m = 2a +1 and n = 2b+1 where a and b are non-negative integers that determine how far the filter extends from its center. The size of a filter (kernel) is defined and expressed as m x n, where m and n are odd integers, such as 3 × 3 or 5 × 5.

correlation

Process of moving a filter mask over the image and computing the sum of the product of corresponding values (image pixel values and filter values) at each position.
Result: The sum becomes the value of the pixel in the output image

convolution

Similar to correlation, but the filter is first rotated by 180 degrees (Flipped both horizontally and vertically) before the computation.
Result is calculated using the same process as correlation (multiplying and summing), resulting in a new pixel value for the output image.

how does an original filter look like after 180 degree rotation for convolution

After 180 degree rotation:

the terms convolution filter or convolution mask may denote:

whether we use a correlation or convolution

smoothing filters

Used for blurring an image

blurring

used in preprocessing steps such as:

• removal of small details from an image prior to (large) object extraction

• bridging of small gaps in lines or curves

• used for noise reduction

output (response) of a smoothing, linear spatial filter

the avg of the pixels contained in the neighborhood (i.e. 3 × 3) . the result replaces the center pixel of the neighborhood, effectively “smoothing” the image.

Averaging filter

computes the mean (avg) of the pixel values in the neighborhood

common uses for smoothing

• noise reduction (remove unwanted variations)

• simplifying images before further processing, like edge detection or segmentation

side effect of averaging filtering

they blur edges and fine details (you lose some detail in exchange for noise reduction)

irrelevant detail

refers to pixel regions much smaller than the filter size, hence why we smooth them out.

what are order-statistic filters?

they are nonlinear spatial filters that:

• order the pixel values in a neighborhood based on rank (i.e. from smallest to largest)

• replace center pixel value with specific value from ordered list (based on chosen filter)

types of order-statistic filters

median filter (most commonly used)
max filter
min filter

median filter

replaces the center pixel w the median value of the sorted neighborhood

max filter

replaces the center pixel w the max value

min filter

replaces the center pixel w the min value

median filters are particularly effective in the presence of….

impulse noise, aka. salt-and-pepper noise

salt and pepper noise

random pixels in the image appear as either black(salt) or white(pepper).
median filters are effective at removing this noise bc extreme values are discarded during sorting

explain whats happening in the images (from left to right a,b,c)

(a) Original image w salt and pepper noise
(b) Result of smoothing using a 3 × 3 averaging filter. Noise reduced but image still blurry
c) Result of 3 × 3 median filter. Noise effectively removed without any more blurring.

median filter vs averaging filter

preserves edges bc they do not average pixel values
eliminate noise more effectively, especially when the noise is impulsive (salt and pepper)

sharpening

highlight fine detail or to enhance detail in an image which may have been blurred

sharpening could be accomplished by

spatial differentiation

foundation

foundation of sharpening lies in detecting changes in pixel intensity (fine details, edges)
sharpening works by enhancing high-frequency components (edges) and making the transitions in intensity more pronounced

to undetstand sharpening: how does derivatives behave in flat segments (constant intensity)

derivative is zero

to understand sharpening: how does derivatives behave in discontinuities (steps or ramps)

• sharp transitions(step changes): derivative is large

• ramps(gradual changes) derivative has a constant non-zero value.

• gray level ramps; derivative captures the rate of change along sloping regions

first order derivative

measures rate of change in intensity between two points and its used for detecting edges and sharp transitions in an image

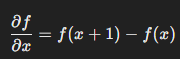
second order derivative

measures the rate of change of the first order derivative (i.e. how quickly the edges change)
used for emphasizing edges and finding zero crossings

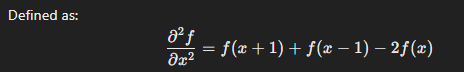
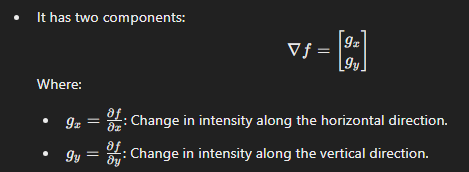
gradient (first order derivative for image sharpening)

represents the direction and rate of change in pixel intensity

magnitude of gradient (overall rate of change calculation)

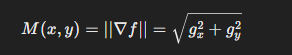
most used gradient masks

Prewitt and Sobel

The Laplacian (second order derivative for image sharpening)

laplacian measures the second derivative of intensity changes in an image