Statistics Final Flashcards (ST 311 NCSU)

Statistics

the science of planning studies and experiments, obtaining data, and organizing, summarizing, analyzing, and interpreting those data and then drawing conclusions based on them

Conducting a statistical study includes 3 phases:

1. Prepare: consider the population, data types, and sampling method

2. Analyze: describe the data you collected and use appropriate statistical methods to help with drawing conclusions

3. Conclude: using statistical inference, make reasonable judgements and answer broad questions

Data

collections of observations, such as measurements, counts, descriptions, or survey responses

Population

the complete collection of all measurements or data that are being considered. Typically, a population is the complete collection of all data we would like to better understand or describe. We also call it the population of interest

Sample

a subset of members selected from a population (random)

Parameter

a numerical measurement describing some characteristic of a population

Statistic

a numerical measurement describing some characteristic of a sample

Quantitative (numerical) data

consists of numbers representing counts or measurements (2 types: discrete or continuous)

Categorical data (qualitative)

consists of names or labels (NOT numbers)

Discrete data (quantitative)

result when the data values are quantitative and the number of values is finite or countable (ex: # of tosses of a coin before getting tails)

Continuous data (numerical)

result from infinitely many possible quantitative values where the collection of values is not countable (ex: the arm spans in inches of high school seniors)

Our goal is to answer a question about a ___

population

We want our sample to be random and ___ of the population

representative

Simple Random Sample (SRS)

A sample of n subjects is selected in such a way that every possible sample of the size size n has the same chance (probability) of being chosen

Stratified Sample

Subdivide the population into 2+ subgroups (or strata) so that the subjects in the same subgroups share the same characteristics. Then draw a sample from each subgroup. The number sampled from each stratum may be done proportionally with respect to population size.

Cluster Sample

Divide the population area into naturally occurring sections (or clusters), then randomly select some of these clusters and choose all the members for those selected clusters)

Systematic Sample

select some starting point and then select every kth element in the population. Works well when units are in the same order like an assembly line

Multistage sample

Collect data by using some combination of the basic sampling methods

Convenience Sampling

Select the first k # of subjects that you come across

Bad Sampling Frame

When attempting to list all members of a population, some subjects are missing. It can be difficult to make a complete list

Non-response bias

Some part of the population chooses not to respond, or subjects were selected but are not able to be contacted

Response bias

Responses to questions are not truthful. This may occur when people are unwilling to reveal personal matters, admit to illegal activity, or tailor their responses to “please” the investigator

Wording and Order Bias

The way questions are worded may be leading/inflammatory to elicit a response. Or the order of questions influences answers.

Measure of center

a value at or near the center or middle of a data set, “typical” values for a group

EX: mean, median, mode

Σ

denotes a sum, “sigma”

x

denotes individual data value

n

denotes # of values in a sample, “sample size”

N

denotes number of values in a population

x̄

denotes the same mean, “x bar”

μ

denotes the population mean, “mew”

Mean

found by adding all values and dividing by the number of values in the set. A sample mean is the mean of a sample. A population mean is the mean of an entire population.

Median

the value that is in the middle when listed in ascending order. Shows what # separates the bottom 50% of the data from the top 50%. Roughly half of all values are below, and half are above it.

Mode

the value that occurs with the greatest frequency. Could be no mode. One mode: unimodal, two modes: bimodal, 2+ modes: multimodal

Histogram

the graph of a frequency distribution, a graph of bars of equal width drawn adjacent to each other, a horizontal scale representing classes of quantitative data values, a vertical scale (height) represents frequency

Dotplot

shows each value in a dataset as a dot above a number line

Measures of variation (or spread)

Range, IQR, variance, standard deviation

Range

max data value - min data value (highly affected by outliers)

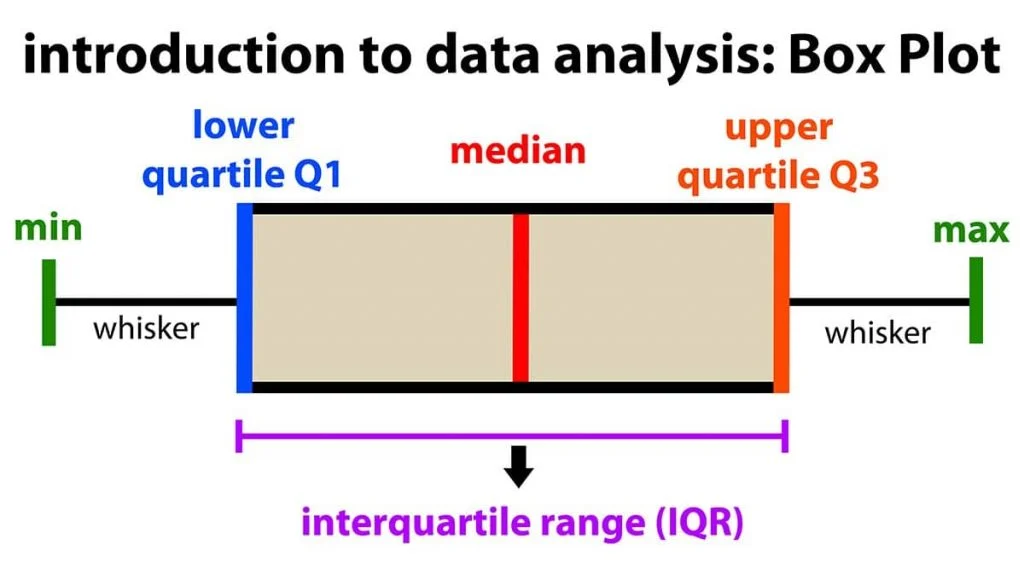
Interquartile Range (IQR)

uses quartiles to provide a range of values that are not as affected by potential outliers as the range

(Q1, Q2, Q3)…1/4 of the data lies between 2 consecutive quartiles

IQR= Q3-Q1

3 IQR quartiles together with the min and max values constitutes the 5-number summary:

1. minimum

2. Q1 (median of the first half of the dataset)

3. Median

4. Q3 (median of the second half of the dataset)

5. Maximum

Variance

(Standard deviation)²

Standard deviation

sqrt(variance)

Defined as a measure of how much data values deviate from the mean, the value of it is never negative, zero ONLY when data is all the same, larger values indicate greater amounts of variation, SD can increase a lot with one or more outliers, units of SD are the same as the units of the OG data values

a²

Population variance

σ or s

standard deviation

s²

sample variance

Experiment

the process of applying some treatment and then observing the effect

• almost always compares 2+ groups: treatment and control group

• the individuals in an experiment are called units

Control group

no treatment

Units

the individuals in an experiment

Observational study

the process of observing and measuring specific characteristics without attempting to modify the individuals studied

• tell “what’s happening” and can’t describe cause-effect relationships

• accessing reliable records counts as observational

Response variable

measures outcome of a study

explanatory variable

explains/influences changes in the response variable

Design of experiment

plan for collecting the sample

Treatment

a specific experimental condition applied to the units/subjects

Variability in Experiments

There will be variability from treatment effects, experimental error, lurking variables, and confounding variables

Treatment effects

different treatments cause different outcomes

Experimental error

variability among observed values of the response variable for units receiving some treatment, small as possible

Lurking variables

a variable not among the explanatory variables in a study but has impact

Confounding variables

2 variables confounded when the effects on the response variable can’t be distinguished

Principles of Experiment Design

Control, randomization, and replication

Control

Control the effects of lurking/confounding variables by carefully planning

Randomization

randomly assign experimental units to treatments to decrease bias

Replication

measure the effect of each treatment on many units to increase chance variation

Completely Randomized Design

participants randomly assigned to treatments, so lurking variables affect each group equally

Randomized Block Design

the experimenter divides participants into subgroups called blocks, so variability in blocks is less than between blocks. Then, part of each block are randomly assigned to treatment groups.

Matched Pairs Design

a special case of randomized block design; used when only 2 treatment groups are present. Participants grouped in pairs on one or more blocking variables. Then, in each pair, participants randomly assigned to different treatments

Placebo

false drug that subjects believe is real

Placebo effect

tendency to react to a drug/treatment regardless of function

Bias of Subjects

subjects may want to please researcher/hope for specific outcome (Hawthorne Effect, when people behave differently b/c they know they are being watched)

Bias of Researchers

people behave in ways that favor what they believe; researchers may assign subjects to groups/report results in a bias way

Blinding

when individuals in experiments are not aware of how subjects are assigned, so they are less likely to respond with bias

Single-blind study

those who could influence the results are blinded

Double-blind study

those who evaluate the results are blinded too

z-score

the number of standard deviations away from the mean a certain data value is

positive z-score

data value is above average

negative z-score

data value is below average

Standardizing

the process of converting a data value (often labeled x) to a z-score

𝑧 = (𝑥−𝜇) / 𝜎

converting x-value to z-score

Empirical Rule

When a distribution is bell-shaped/normal, the mean and standard deviation have the following relationship:

99.9% of the data is within 3 standard deviations of the mean, 95% of the data is within 2 SD’s, and 68% of the data is within 1 SD of the mean (34% is within -1 SD, 34% is within +1SD).

The 34, 14, 2.5 rule

Significantly low value

values are generally considered significant or unusual if they are (u-2a) or lower

Significantly high value

values are generally considered significant or unusual if they are |u + 2a | or higher

Values not significant

between (u-2a) and (u + 2a)

We will use a significance % of ___ as a general guide for significant values

5%

Density curve

If we scale the bell curve model so the area under the curve = 1

Probability, in a contin. prob. distri., is consequently the ____ the density curve.

area under

Probability Statement

P (small # </= x </= bigger #)

The graph of a normal distri. is called the

normal curve

In a normal curve…

The mean, median, and mode are EQUAL

The normal curve is bell-shaped and is symmetric on the mean..

The total area under the normal curve is EQUAL TO 1.

The normal curve approaches, but never touches, the x-axis as it extends further away from the mean.

Distribution of z-scores

Standard normal distribution

Notation

X ~ N(u, σ) where the ~ symbol reads “is distributed

The random variable X is distri. normally with mean u and SD σ and

Z ~ N(0,1)

Distribution

describes the possible values of a variable, how often they occur, and what pattern they create

Probability description

does the same thing as other distributions but describes how likely (instead of how often) the values of the variable are to occur)

Continuous Random Variable

has an uncountable number of possible outcomes, represented by an interval on the number line

Discrete Random Variable

has a finite or countable number of possible outcomes that can be listed. Countable refers to the fact that they might be infinitely many values, but they can be associated with a counting process.

Criteria for Binomial Distribution

1. There are a fixed number of trials/observation. Labled n.

2. The trials are independent (the outcome of any individual trial doesn’t affect the probabilities in the other trials)

3. Each outcome can be classified as a success or failure. The outcome that a random variable is counting is labeled the success.

4. The probability of a success is constant for each trial. The probability of success is denoted by P(S) = p.

Binomial Notation

X ~ Bin (n,p)

parameters of the distribution

number of trials (n), probability of success (p)

Expected Value

E(x), mean of a random variable

The expected value of a random variable is a ___

weighted mean of the outcomes

The expected value of a discrete random variable is equal to the ____ of the random variable

mean

Binomial Variance

σ² = n x p x q where q = 1-p