Chapter 2

Charateristics of an automaton

An automaton has a set of states and its ‘control’ moves from state to state in response of external inputs.

The control can be

• deterministic: the automaton cannot be in more than one state at any one time. On each input there is one and only one state to which the automaton can transition from its current state. Finite automata refer to deterministic automata

• nondeterministc: it may be in several states at once. Nondeterminism allows us to program solutions to problems using a higher-level language

The nondeterministic automaton is compiled by an algorithm into a deterministic automaton that can be executed on a conventional computer

Two kinds of actions that must be ignored (not in syllabus)

• Actions that are irrelevant to the partecipant involved

• Actions that must not be allowed to kill an automaton

Definition of a deterministic finite automata (DFA)

A DFA consists of

• a finite set of states (Q)

• a finite set of input symbols (big sigma)

• a transition function that takes as arguments a state and an input symbol and returns a state (delta)

• a start state, one of the states in Q

• a set of final or accepting states F. F is a subset of Q

Language of the DFA

The set of all strings accepted by the DFA. That is, the set of strings that take the start state q0 to one of the accepting states. If the language L is the language of a DFA, we say L is a regular language

Transition diagram

• For each state in Q there is a node

• For each state q in Q and each input sybol a in big sigma, let delta(q, a) = p. Then the transition diagram has an arc from node q to node p, labeled a. If there are several input symbols that cause transitions from q to p, then the transition diagram can have one arc, labeled by the list of these symbols

• There is an arrow into the start state q0, labeled Start. This arrow does not originate at any node

• Nodes corresponding to accepting states (those in F) are marked by a double circle. States not in F have a single circle

Transition table

• rows represent states

• columns represent inputs

• the start state is marked with an arrow

• accepting states are marked with a star

Definition of a NFA

A NFA is presented like a DFA. It has

• a finite set of states

• a finite set of input symbols

• a start state, which is a member of Q

• a subest F of Q that includes the final states

• a transition function

Transition function: difference between DFA and NFA

the only difference between an NFA and a DFA is in the type of value that the function returns: a set of states in the case of an NFA and a single state in the case of a DFA

Language of an NFA

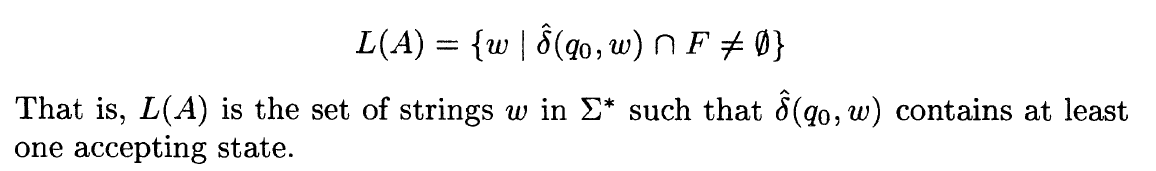
Languages described by some NFA can also be described by some DFA?

Yes. Moreover, the DFA in practice has about as many states as the NFA, although it often has more transitions. However, exponential growth in the number of states is possible

Theorem about languages of a DFA constructed from an NFA (with proof)

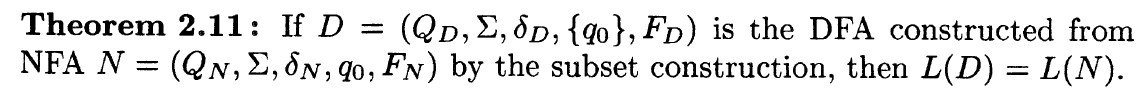
Theorem about languages accepted by NFA and DFA (with proof)

A language L is accepted by some DFA if and only if L is accepted by some NFA.

Definition of epsilon-NFA

A = (Q, alphabet, delta, q0, F), but delta is now a function that takes as arguments:
1. A state in Q and
2. A member of alphabet union {epsilon}