Equilibrium potential, Conservation of Charge, A simple cell model, Ion pumps (2.3 - 2.6)

What is the principle of electrical neutrality?

The principle of electrical neutrality states that the bulk concentration of positively charged ions must equal the bulk concentration of negatively charged ions within any compartment.

How is charge neutrality maintained in biological systems?

In biological systems, the concentrations of positive and negative ions balance each other to maintain charge neutrality. For example, the intracellular fluid (ICF) has high K^+ and negatively charged proteins, while the extracellular fluid (ECF) has high Na^+ and Cl^-.

How does electrical neutrality influence ion concentrations in a cell?

Electrical neutrality ensures that the intracellular concentrations of ions balance each other. For example, if the intracellular concentration of Na^+ is 50 mM and P^+ (organic molecules) is 100 mM, the intracellular concentration of Cl^- must be 50 mM to balance the total positive charge.

What happens if the conservation of charge is violated?

Violations of charge conservation, such as an imbalance of ions across the membrane, can create an electrical potential difference, which is essential for processes like nerve signaling and muscle contraction.

What is the role of concentration balance in conservation of charge?

Concentration balance ensures that the total ion concentration inside and outside the cell remains consistent. For instance:

[Na^+]_{ECF} + [Cl^-]_{ECF} = [Na^+]_{ICF} + [Cl^-]_{ICF} + [P^+]_{ICF}

How does charge and concentration balance determine ion concentrations in a simple cell model?

In a cell with Na^+, Cl^-, and P^+ intracellularly (ICF) and Na^+ and Cl^- extracellularly (ECF), the following equations apply:

1. From charge balance:

[Cl^-]_{ICF} = [Na^+]_{ICF} = 50\ \text{mM}

[Cl^-]_{ECF} = [Na^+]_{ECF}

2. From concentration balance (osmotic equilibrium):

[Na^+]_{ECF} + [Cl^-]_{ECF} = [Na^+]_{ICF} + [Cl^-]_{ICF} + [P^+]_{ICF}

Substituting values:

2 \cdot [Na^+]_{ECF} = 50\ \text{mM} + 50\ \text{mM} + 100\ \text{mM}

[Na^+]_{ECF} = [Cl^-]_{ECF} = 100\ \text{mM}

Key Insight: Unlike osmotic balance, where solute concentrations are equal, charge balance ensures that Cl^- concentrations differ across the membrane due to the presence of impermeable P^+ molecules intracellularly.

What are the updated equilibrium conditions? (version 3)

1. Osmotic equilibrium (total solute concentration): The osmotic pressures inside and outside the cell must balance to prevent water movement across the membrane.

2. Charge balance: The total positive and negative charges in any compartment (either inside or outside the cell) must be equal to maintain electrical neutrality.

3. Concentration equilibrium: Permeable solutes must have equal concentrations on both sides of the membrane to avoid net diffusion. (this can be overridden due to the charge balance condition).

What is the equilibrium potential for a single ion?

The equilibrium potential for an ion is the electrical potential difference across a membrane that would exactly balances the concentration gradient for that ion, calculated using the Nernst equation:

E_X = V_{\text{in}} - V_{\text{out}} = \frac{RT}{zF} \ln \left(\frac{[X]_{\text{out}}}{[X]_{\text{in}}}\right)

where:

- R = gas constant,

- T = absolute temperature (Kelvin),

- z = ion valence,

- F = Faraday’s constant,

- [X]_{\text{in}} and [X]_{\text{out}} are the ion concentrations inside and outside the cell.

What is the simplified Nernst equation at standard room temperature?

At standard room temperature, the Nernst equation simplifies to:

E_X = \frac{58\ \text{mV}}{z} \log_{10}\left(\frac{[X]_{\text{out}}}{[X]_{\text{in}}}\right)

This uses a base-10 logarithm instead of the natural logarithm.

What is the relationship between the equilibrium potential and membrane potential for multiple ions?

For a system with two permeable ions (e.g., K^+ and Cl^-) and the system is in equilibrium, the membrane potential E_m must satisfy the equilibrium conditions for both ions. As there can only be a single potential across the membrane known as the membrane potential, E_m, both equilibrium potentials have to equal this, resulting in the Donnan equilibrium:

E_m = 58\ \text{mV} \log_{10} \left(\frac{[K^+]_{\text{out}}}{[K^+]_{\text{in}}}\right) = -58\ \text{mV} \log_{10} \left(\frac{[Cl^-]_{\text{out}}}{[Cl^-]_{\text{in}}}\right)

This implies:

\frac{[K^+]_{\text{out}}}{[K^+]_{\text{in}}} = \frac{[Cl^-]_{\text{in}}}{[Cl^-]_{\text{out}}}

Concentrations must reflect these ratios for there to be equilibrium.

What does the Donnan equilibrium describe?

The Donnan equilibrium (or Gibbs-Donnan equilibrium) describes how ion concentrations and membrane potentials equilibrate when multiple ions can move across the membrane, maintaining both charge and concentration balance.

What are the updated equilibrium conditions? (version 4)

1. Osmotic equilibrium (total solute concentration): The osmotic pressures inside and outside the cell must balance to prevent net water movement. If membrane not permeable to water, then condition can be ignored.

2. Charge balance/electrical neutrality: The total amount of positive and negative charges within any given compartment (such as the intracellular or extracellular space) must equal one another to maintain electrical neutrality.

3. Concentration equilibrium (replaced by condition 4): Permeable ions have equal concentrations on both sides of the membrane, ensuring no net movement driven solely by concentration differences.

4. Electrochemical equilibrium (Gibbs-Donnan): The combined forces of the concentration gradient and the electrical potential (membrane potential) are balanced, meaning there is no net driving force for ion movement, even if concentrations are unequal.

5. Conservation of Mass (for a box that has two compartments and a membrane): Total mass number for any species can’t change.

Condition 3 can be replaced by condition 4 (the imbalance of concentration is balanced by the potential difference).

What is a simple cell model, and what principles govern it?

A simple cell model represents a cell at equilibrium, containing Na^+, K^+, Cl^-, and negatively charged molecules P^-. It is governed by three principles:

1. Concentration/osmotic balance: Ensures solute concentrations stabilize water movement.

2. Electrical neutrality: Balances total positive and negative charges in each compartment.

3. Gibbs-Donnan equilibrium: Balances the electrochemical potential of permeable ions, satisfying charge and concentration equilibrium.

We later find out sodium ions are actually able to pass through the membrane (contrary to this model), and any sodium gradient would result in ion movement. There is now a need for ion pumps to help maintain the current state of the cell (called a steady-state).

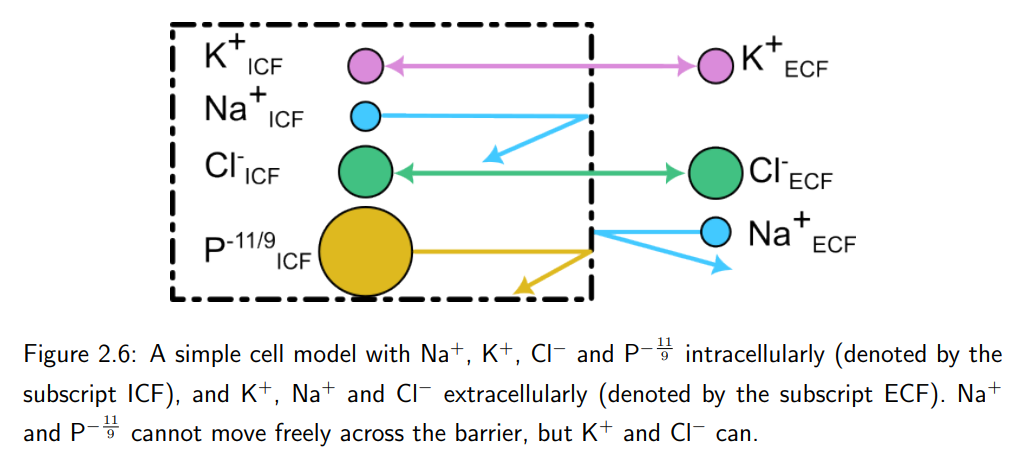
What is the function of ion pumps in cells?

Ion pumps are enzymes that move ions against their concentration or electrical gradient, requiring energy (e.g., from ATP). They maintain ion gradients essential for cell function.

How does the sodium-potassium pump work?

The sodium-potassium pump (Na⁺/K⁺-ATPase) maintains high intracellular K^+ and high extracellular Na^+ concentrations by:

1. Binding Na^+ and ATP inside the cell.

2. Releasing Na^+ outside the cell after ATP hydrolysis.

3. Binding K^+ extracellularly and releasing it inside the cell upon return to the original conformation.

Why is the sodium-potassium pump important?

It prevents sodium from accumulating intracellularly, which would disrupt osmotic balance and cell volume. It also maintains the steady-state membrane potential, allowing cells to remain excitable.

This is a “steady-state”, meaning it requires energy to maintain. If there was no energy expended over time, it would be considered an “equilibrium”.

What is the relationship between ion pumps and steady state?

While equilibrium does not require energy, the steady-state maintained by ion pumps does, ensuring ions like Na^+ and K^+ remain at constant levels despite leaks across the membrane.