AP Precalculus Formula Sheet

Unit One: Polynomial and Rational Functions

1. Average rate of Change: 

• Measures how much the function value changes over an interval relative to the change in x.

2. Increasing/Decreasing Functions:

• Increasing: The function values rise as (x) increases, indicating a positive slope/rate of change.

• Decreasing: The function values fall as (x) increases, indicating a negative slope/rate of change.

• A function is constant if it neither increases nor decreases over an interval.

3. Concavity:

• Concave Up: The graph of the function looks like a smile, indicating that the slope is increasing.

• Concave Down: The graph of the function looks like a frown, indicating that the slope is decreasing.

4. Types of Functions: 

• Linear: constant rate of change; equation is y = mx+b, where m is the slope

• Quadratic: rates of change form a linear pattern; equation f(x) = ax^2 + bx+ c

• Polynomial (degree n): nth (3rd in the graph) order rates of change are constant when x values are evenly spaced.

5. Local (Relative) Maximum/Minimum:

• Maximum: Functions transitions from increasing to decreasing

• Minimum: Function transitions from decreasing to increasing 

6. Point of inflection:

• Point where concavity changes; graph switches from curving upwards to curving downwards and vice versa.

7. Complex Roots:

• If a complex number (z = a + bi)  is a root of p(x), or a polynomial function with real coefficients, its complex conjugate (z = a - bi) must also be a root.

8. Even and Odd Functions:

9. Polynomial End Behavior: 

• Depends on degree and the sign of the leading coefficient

10.  Rational Functions:

• Zeroes of R are zeroes of P that are not also zeroes of Q

11. Hole in the Graph:

• Hole: When both P and Q equal zero at x = c; indicates that the function is undefined, but can often be simplified by canceling common factors.

12. Vertical Asymptote:

• Vertical asymptotes occur at x-values where Q(x) = 0 while P(x) is non-zero.

13.  End Behavior of Rational Functions:

• Indicates whether the rational function approaches 0, infinity, or negative infinity as x approaches positive/negative infinity.

14. Binomial expansion

• Can be found using box multiplication or Pascal’s Triangle

15. Transformations of Functions:

Unit Two: Exponential and Logarithmic Functions:

1. Base Logarithmic Function:

2. Exponential Rules: 

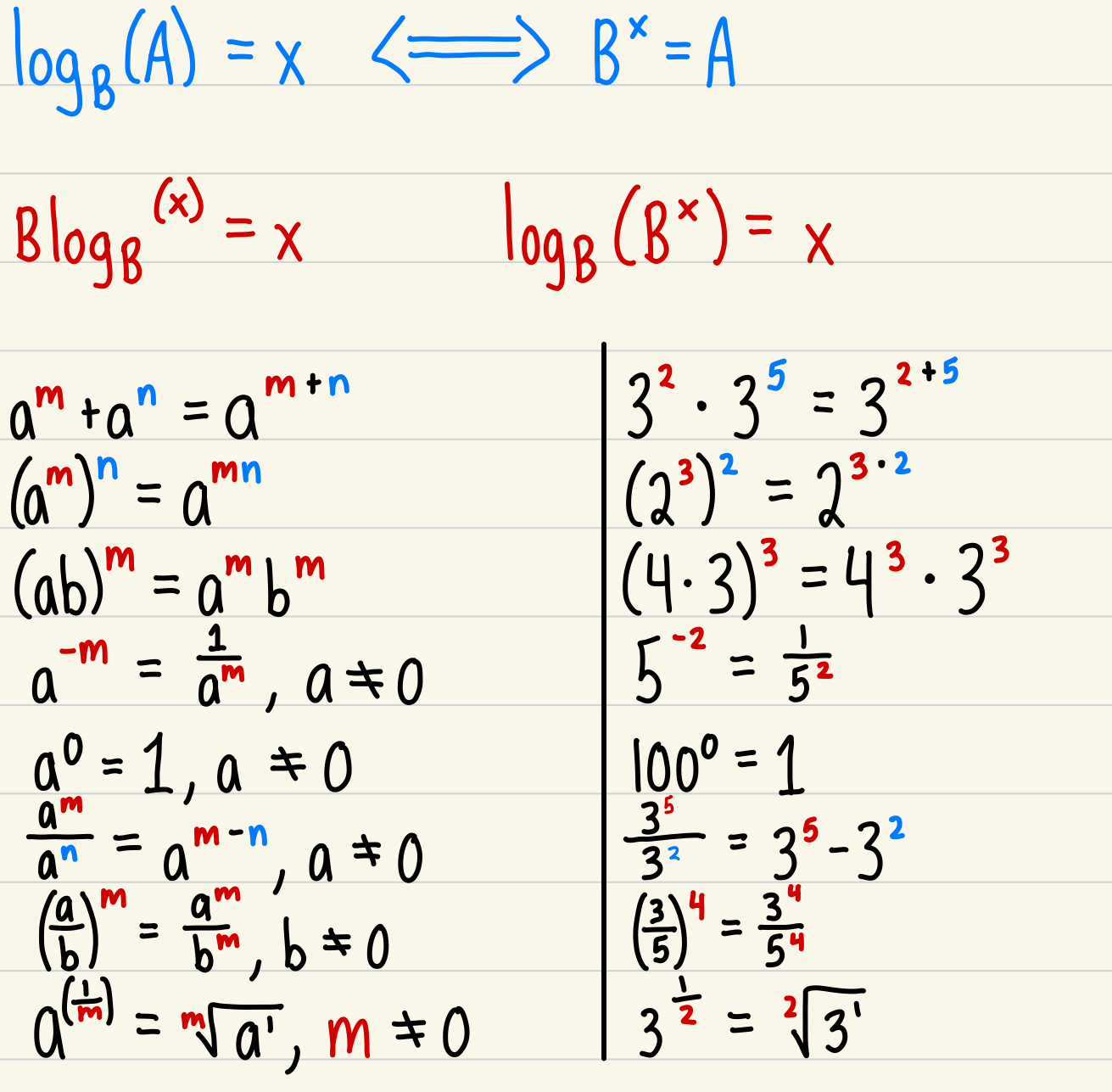
3. Logarithmic Rules:

• When log has no subscript, it is assumed to be 10

• For natural logarithms (ln), they are equal to regular logarithms with the value of e as the subscript.

4. Function Composition: 

5. Function Inverses:

Unit Three: Trigonometry and Polar Coordinates

1. Standard Position:

• Vertex is at the origin and one ray of the angle is on the positive x-axis

2. Arc Length Formula:

3. Unit Circle (Radian Angles): 

4. Sine, Cosine, and Tangent:

5. Special Right Triangles:

6. Trigonometric Identities:

7. Graphs of Trigonometric Functions:

• The equation is y = Asin( B (x + c)) + D where:

• A is amplitude

• The period is equal to 2π/B

• The phase shift is C

• The midline is y = D

8. Vertical Asymptotes:

9. Inverse Trigonometry:

10. Polar Coordinates:

• Important Formulas:

11. Modeling:

• When looking at a semi-log plot where the vertical axis is logarithmically scaled and the graph looks linear, that is an exponential function.

• For a residual plot, pattern means inappropriate and no pattern means appropriate.