Calculus AB Flashcards

sin (0)

0

cos (0)

1

tan (0)

0

sin (π/6)

1/2

cos (π/6)

√3/2

tan (π/6)

√3/3

sin (π/4)

√2/2

cos (π/4)

√2/2

tan (π/4)

1

sin (π/3)

√3/2

cos (π/3)

1/2

tan (π/3)

√3

sin (π/2)

1

cos (π/2)

0

tan (π/2)

undefined

sec (0)

1

sec (π/6)

2√3/3

sec (π/4)

√2

sec (π/3)

2

sec (π/2)

undefined

csc (0)

undefined

csc (π/6)

2

csc (π/4)

√2

csc (π/3)

2√3/3

csc (π/2)

1

cot (0)

undefined

cot (π/6)

√3

cot (π/4)

1

cot (π/3)

√3/3

cot (π/2)

0

|x|/x

±1

√25x²

|5x|

lim θ→0 sinθ/θ

1

lim θ→0 (1-cosθ)/θ

0

sin²θ + cos²θ

1

ln e

1

ln 1

0

x⁵√x³

x¹³/²

factor x³+27

(x+3)(x²-3x+9)

factor x³-64

(x-4)(x²+4x+16)

d/dx ln x

1/x

d/dx e^x

e^x

d/dx √x

1/2√x

d/dx sin(x)

cos(x)

d/dx cos(x)

-sin(x)

d/dx tan(x)

sec²(x)

d/dx sec(x)

sec(x)tan(x)

d/dx csc(x)

-csc(x)cot(x)

d/dx cot(x)

-csc²(x)

d/dx f(x)g(x)

f(x)g'(x)+g(x)f'(x)

d/dx f(x)/g(x)

g(x)f'(x)-f(x)g'(x)/g²(x)

d/dx f(g(x))

f'(g(x))g'(x)

s(t) represents

position function

s'(t) represents

velocity function

s''(t) represents

acceleration function

when can we use dominant term shortcuts to evaluate limits?

when lim x→±infinity

what is the formula we use for the definition of the derivative?

f'(x) = lim h→0 f(x+h)-f(x)/h

what do we have to check as the definition of continuity?

1. lim x→c f(a) exists

2. f(a) exists

3. lim x→c f(a) = f(a)

What three things must be true in order for us to use the Intermediate Value Theorem?

1. continuous on [a,b]

2. f(a)≠f(b)

3. By IVT, there does exist a value c since f(x) takes on all values a < x < b

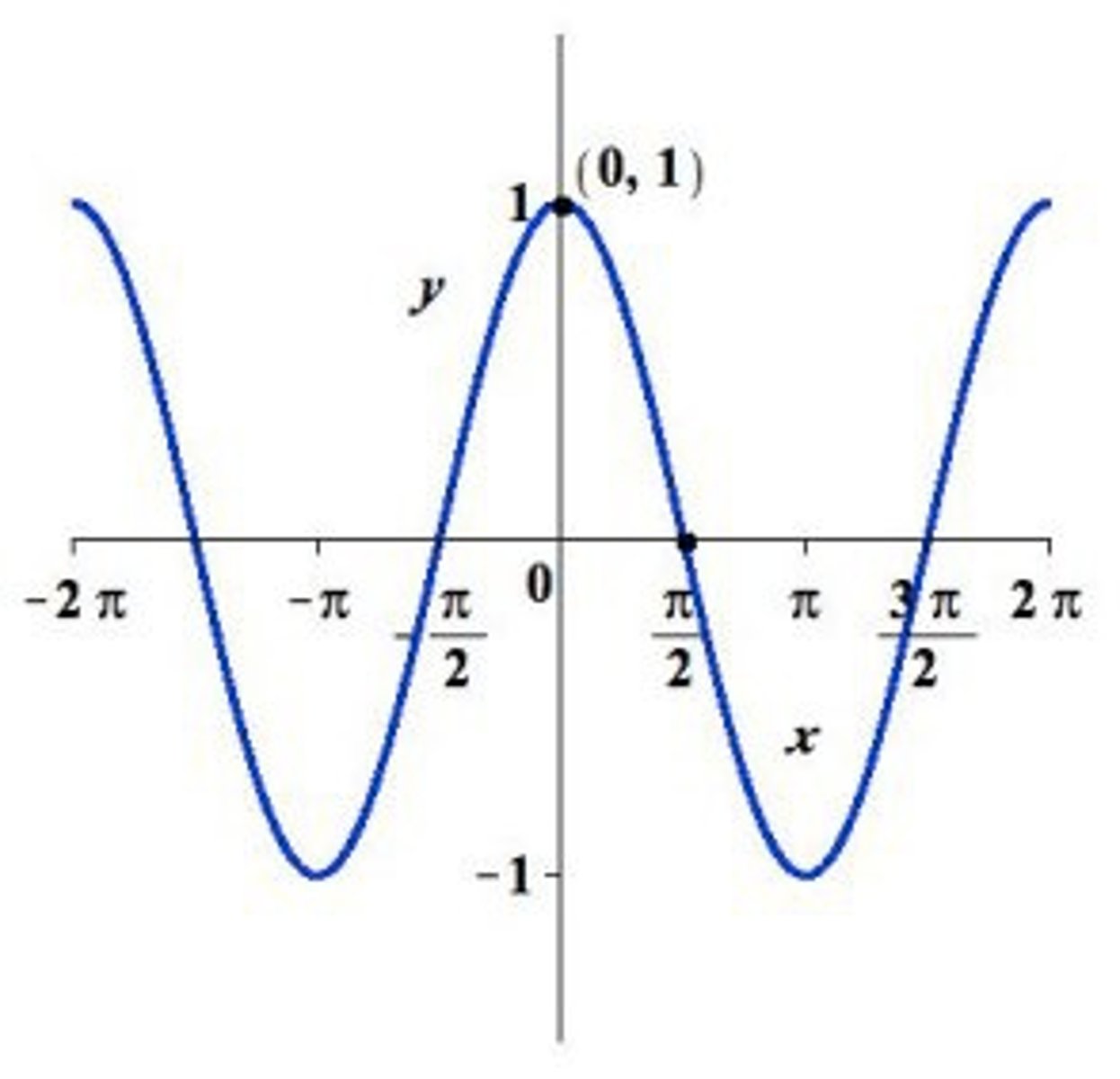
parent function of cos

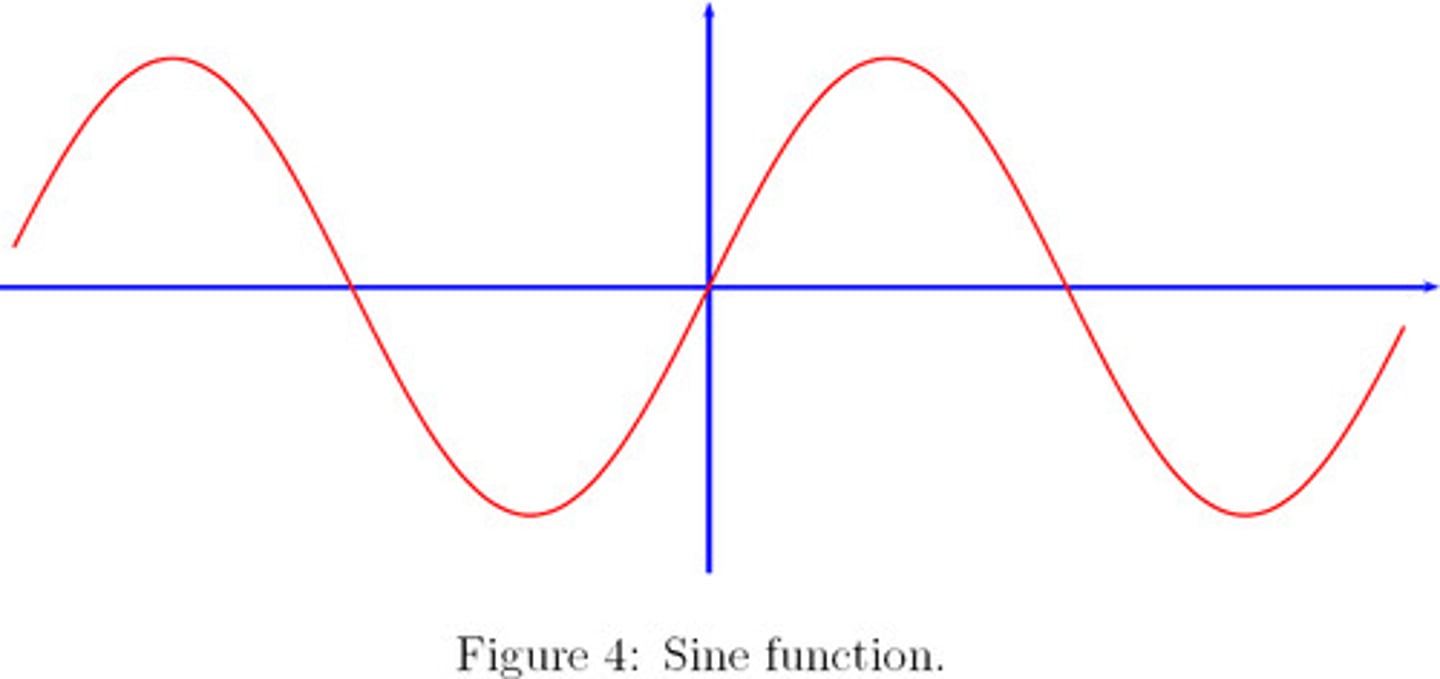
parent function of sin

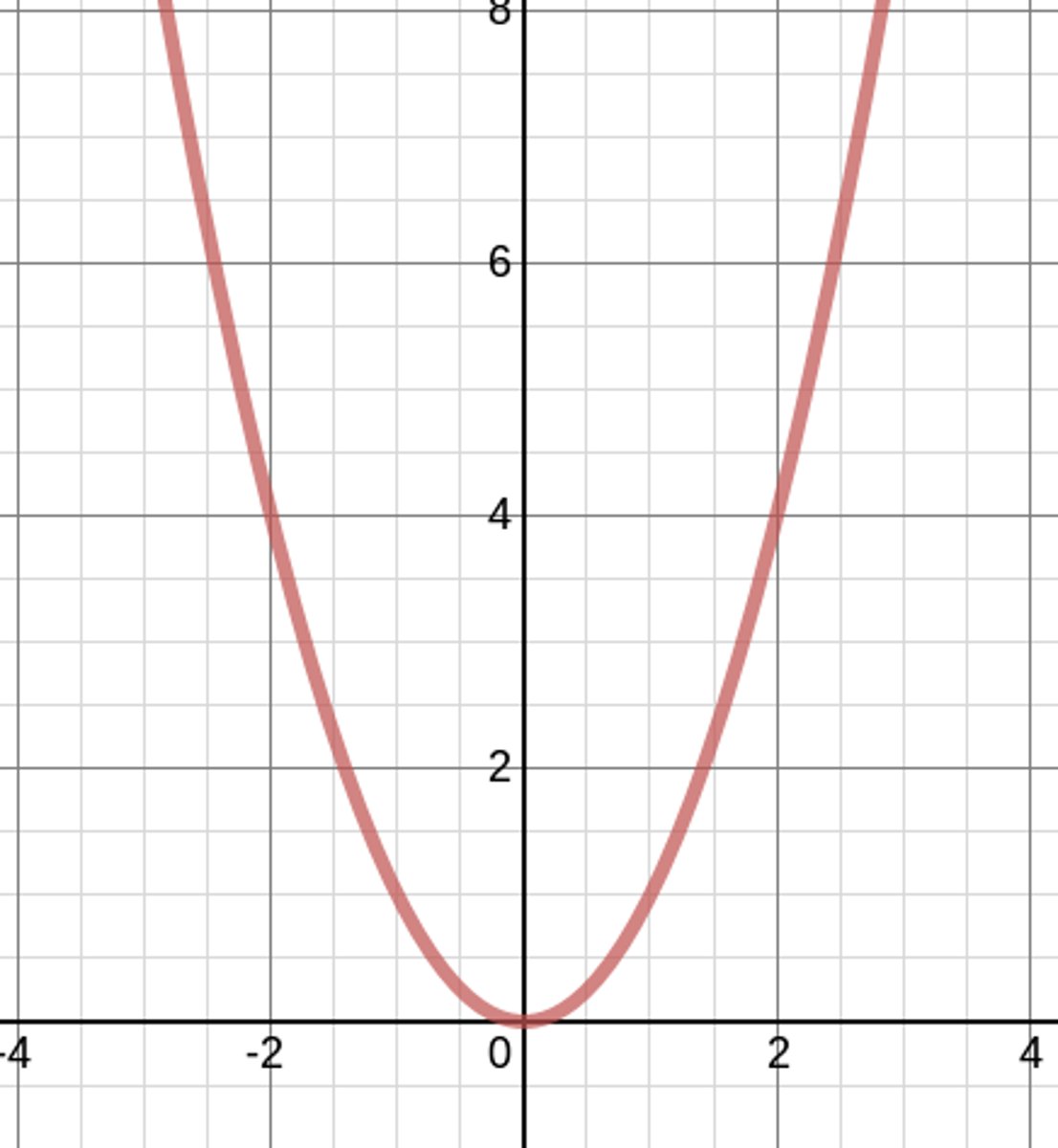
parent function of x²

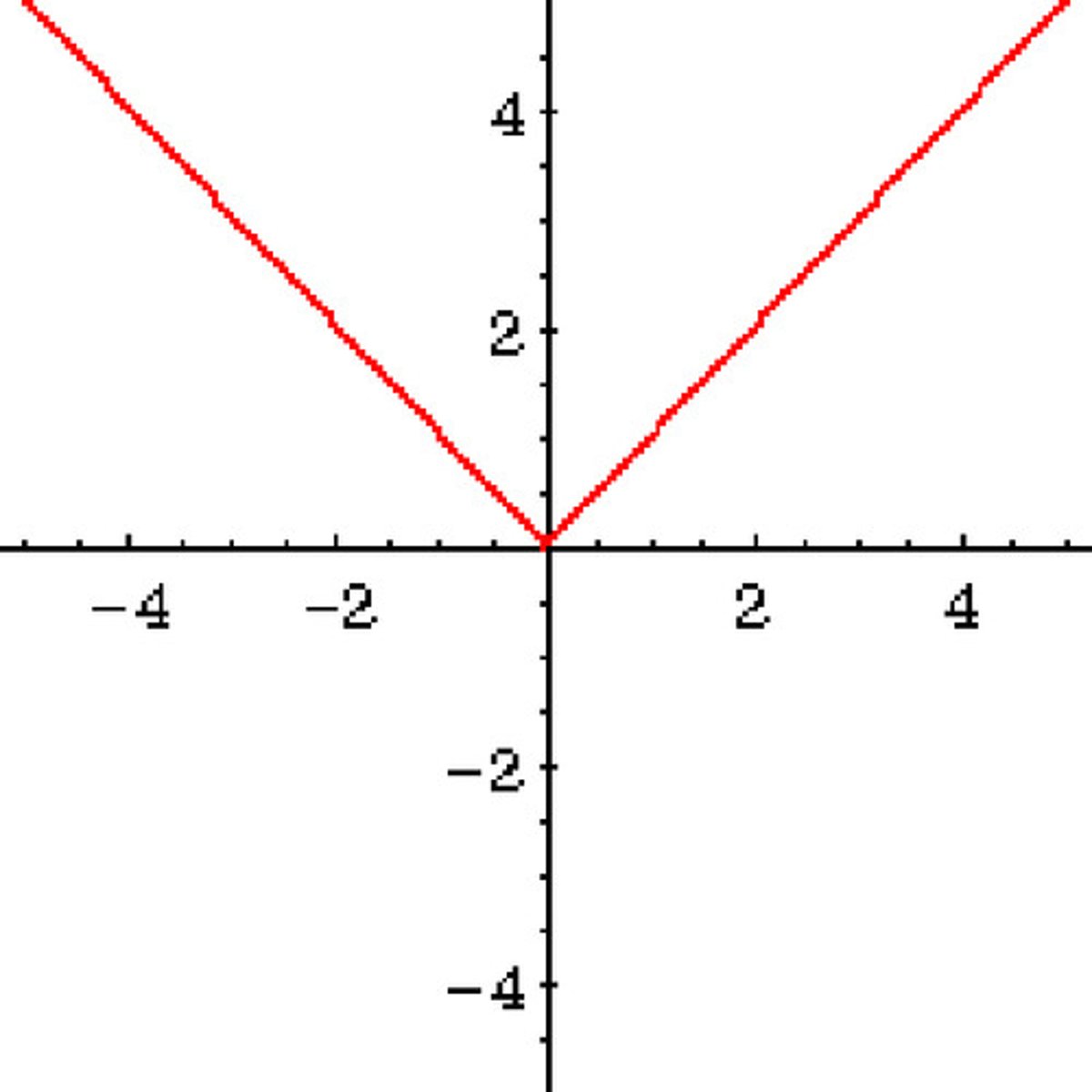
parent function of |x|

parent function of x³

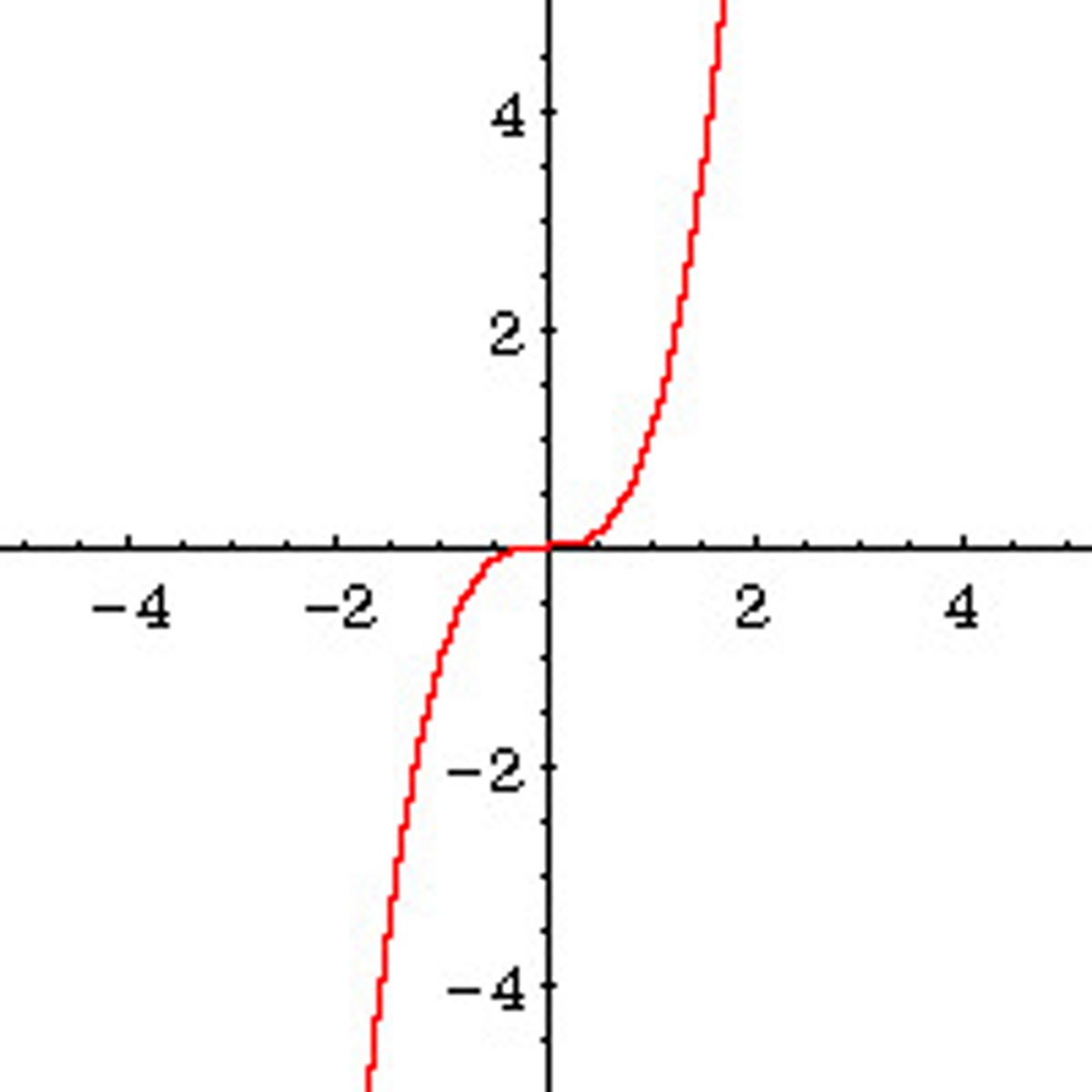
parent function of √x

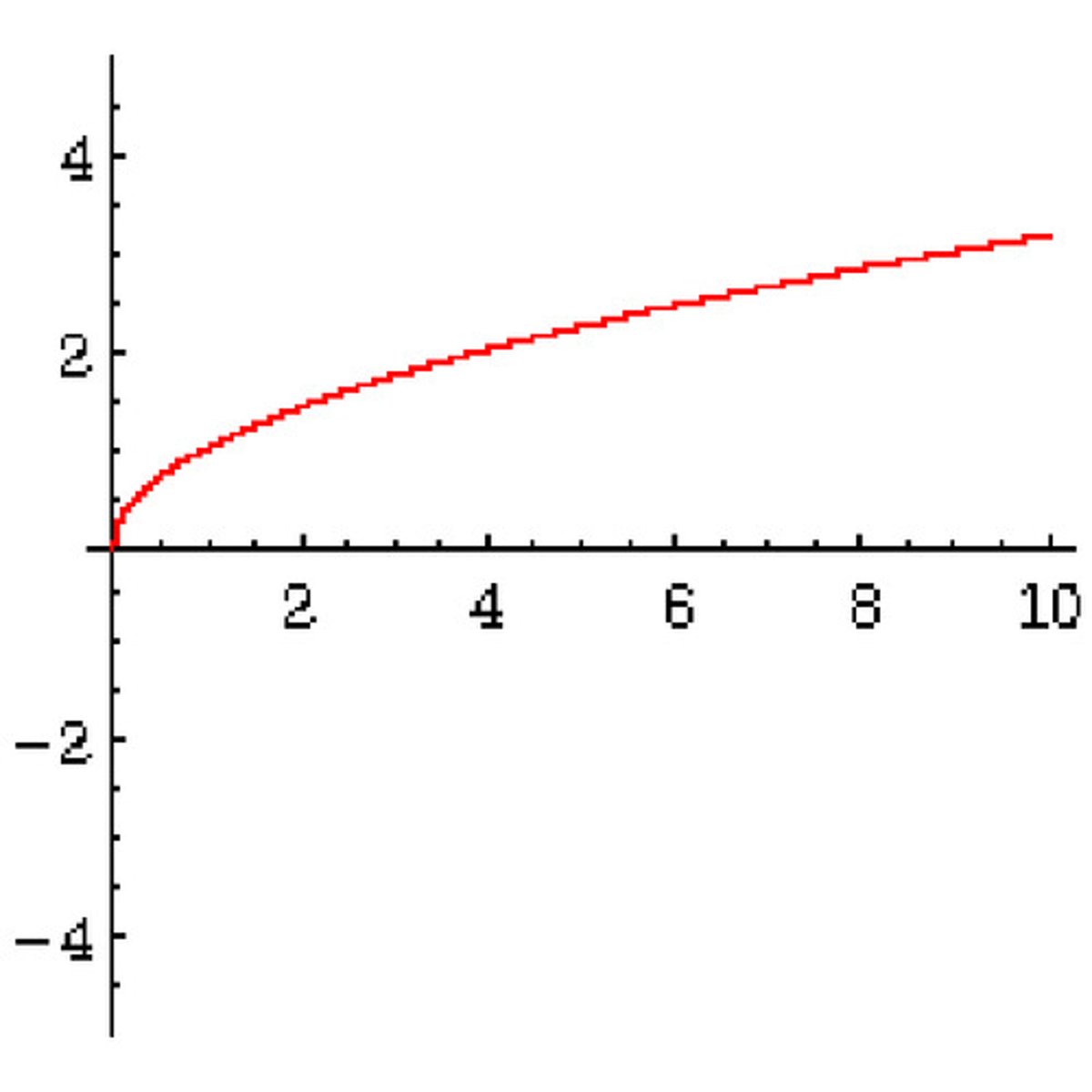
parent function of 1/x (rational function)

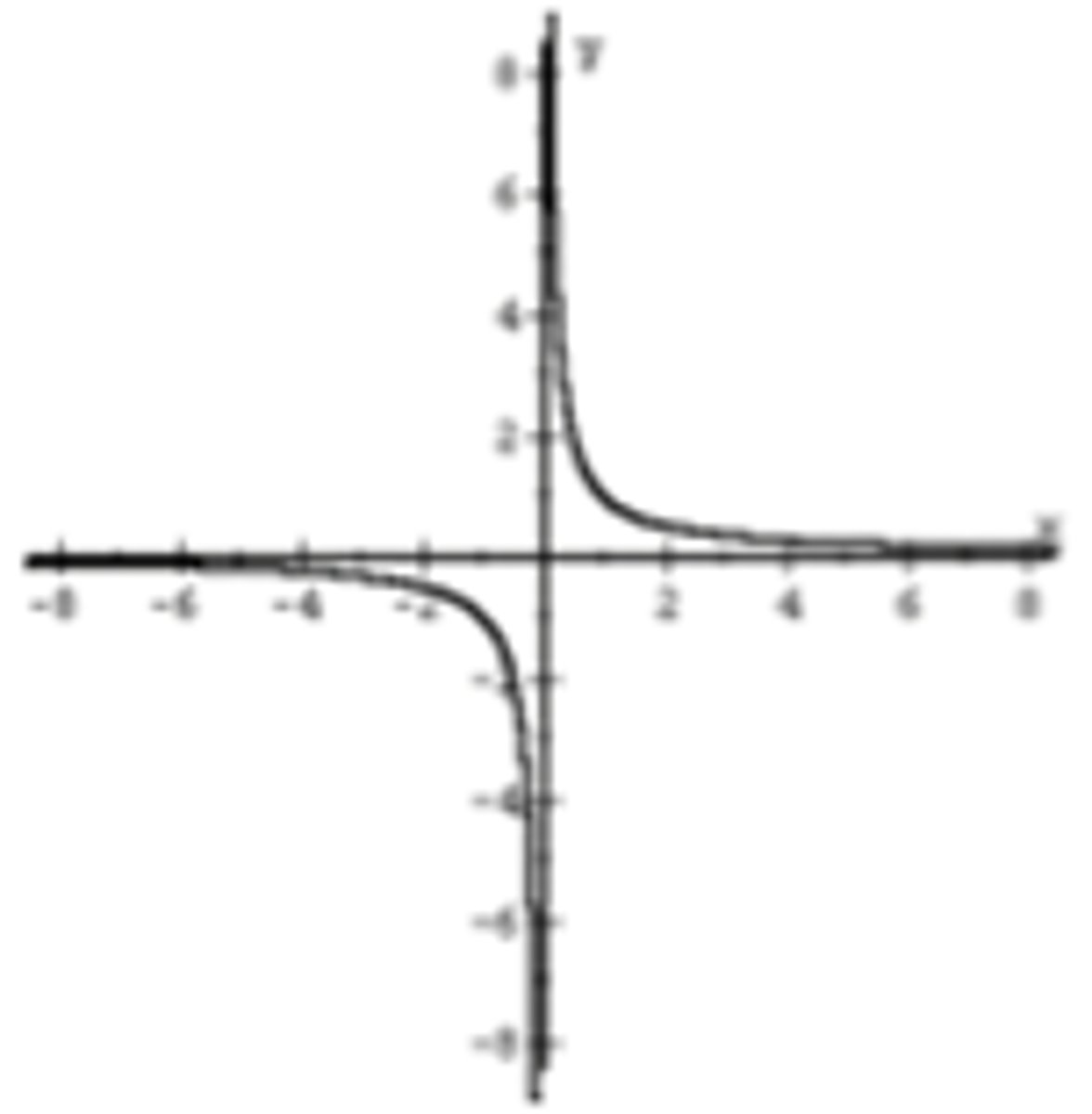
parent function of e^x

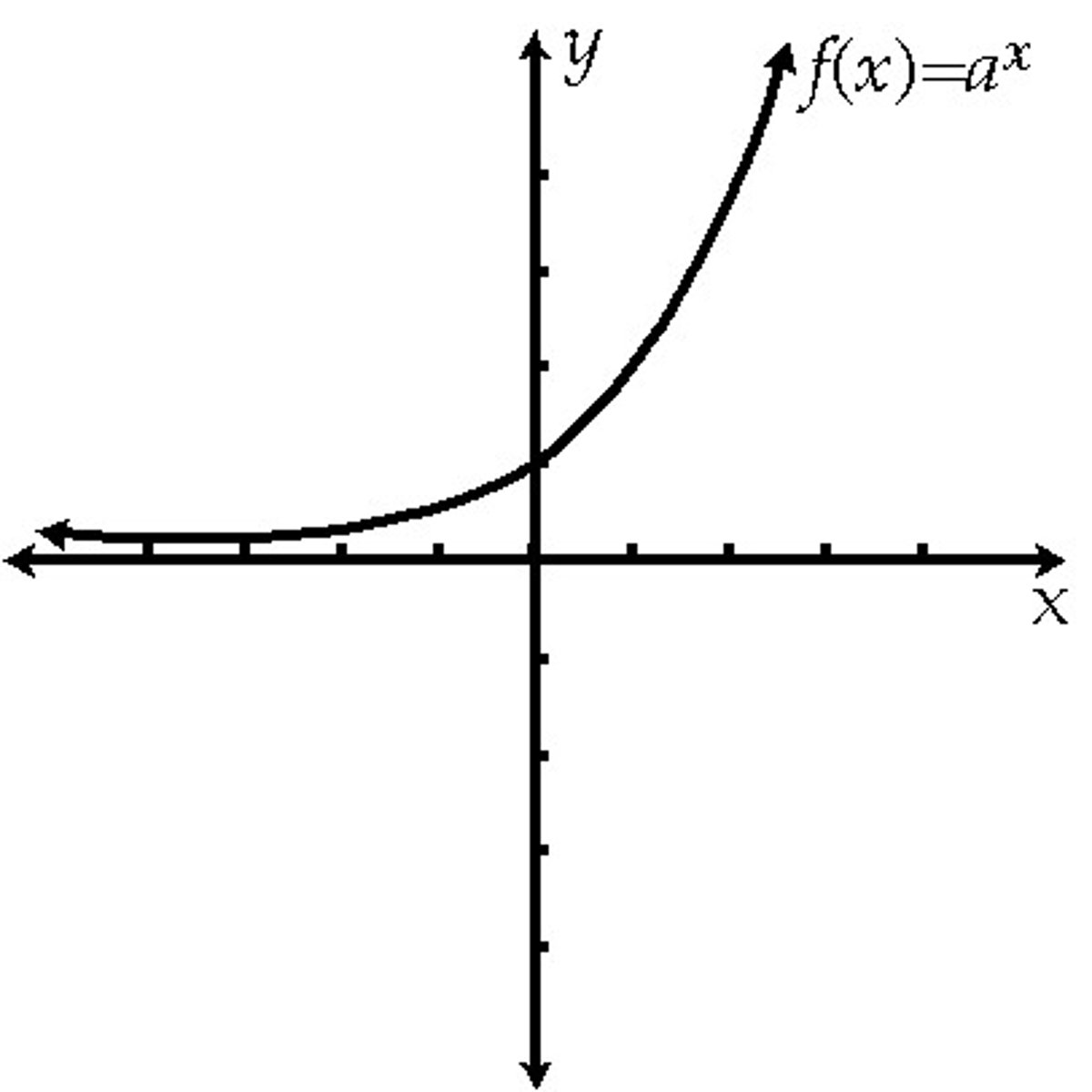
parent function of ln x

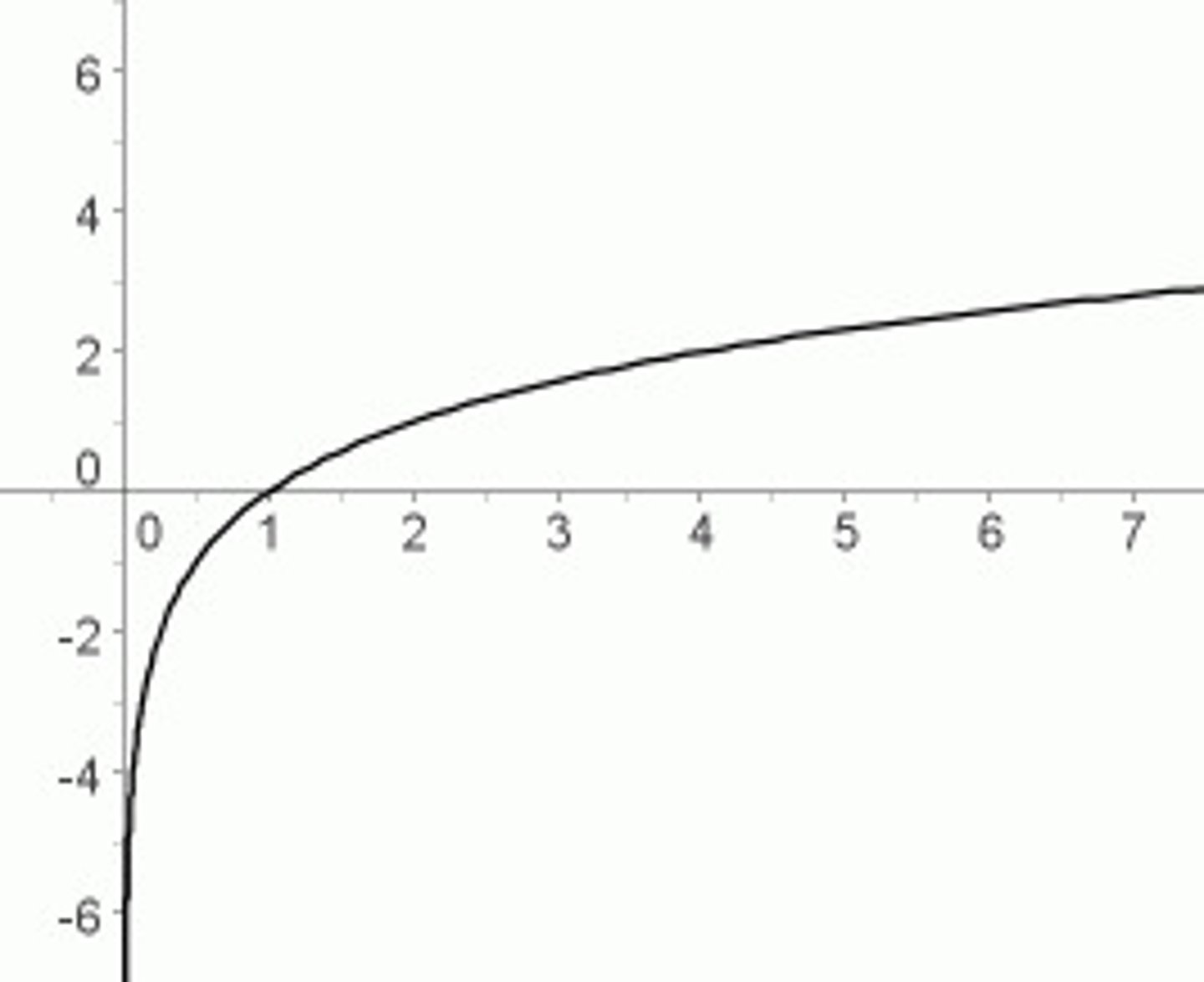
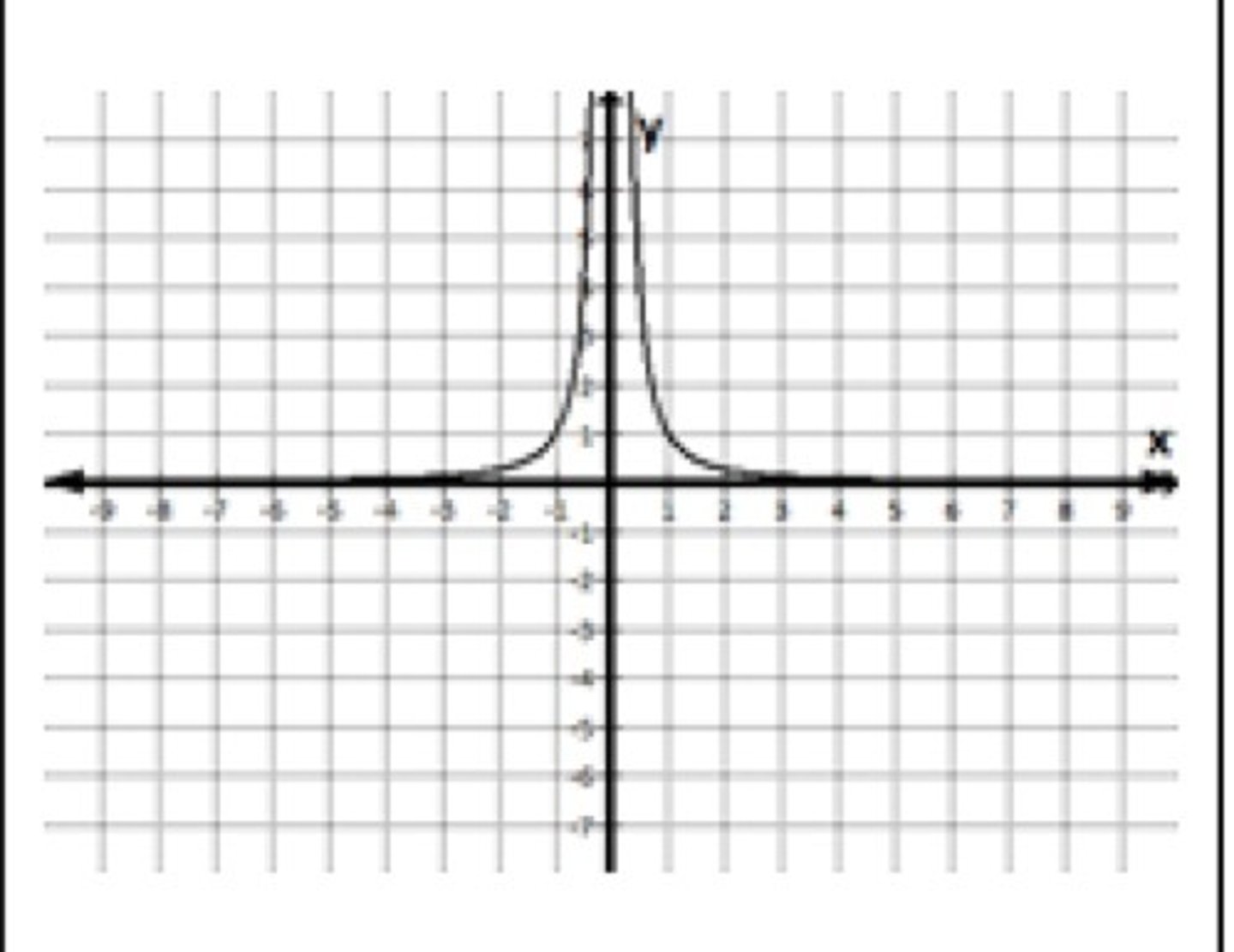
parent function of 1/x²

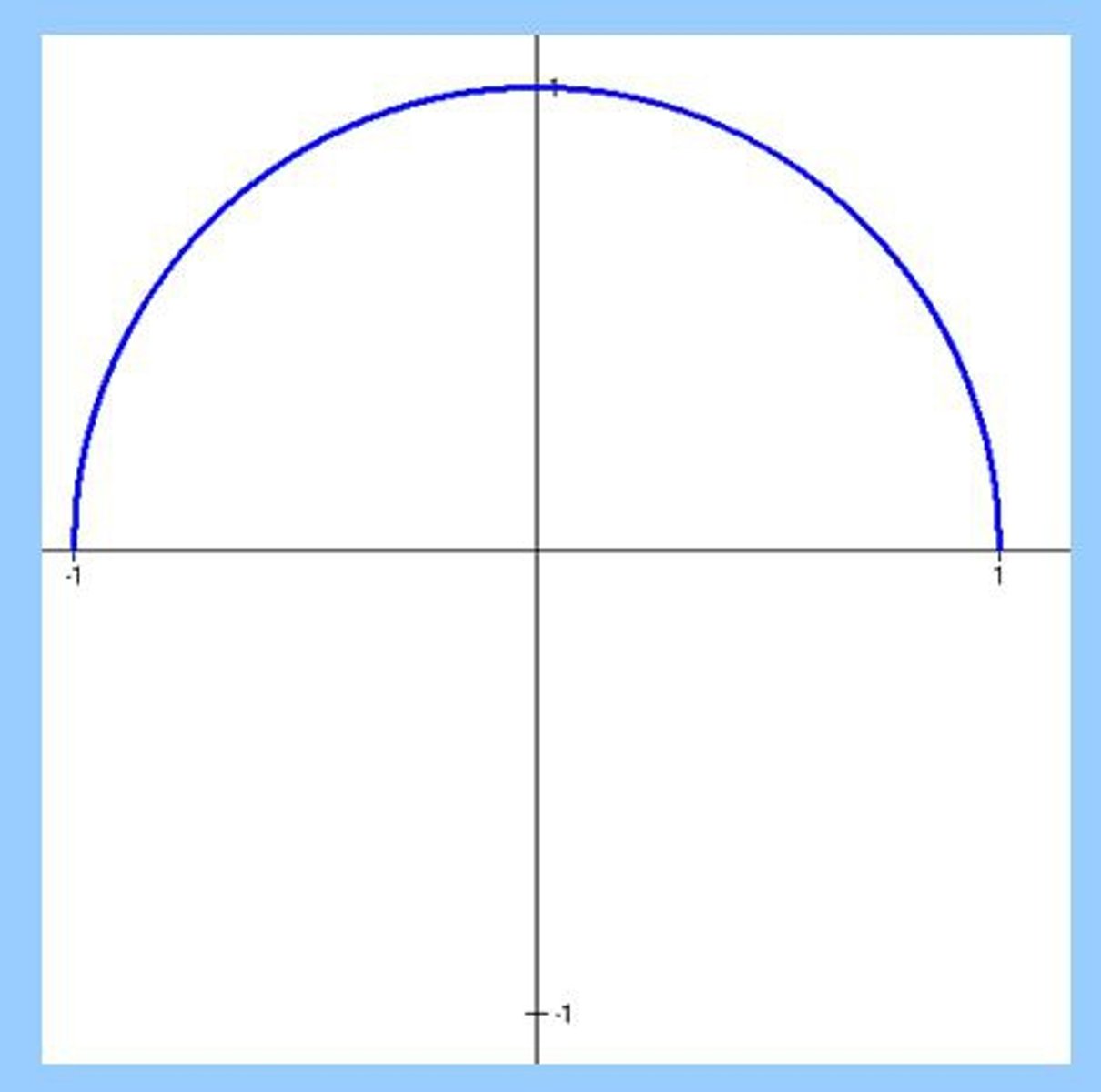
parent function of √a²-x² (semicircle)

√x²

|x|

aroc

f(b)-f(a)/b-a

1/cosx

secx

1/sinx

cscx

1/tanx

cotx

sinx/cosx

tanx

cosx/sinx

cotx

rewrite 5/x² so it is no longer a fraction

5x⁻²

rewrite √x so it has a rational exponent

x½

d/dx √x

1/2√x

rewrite x⁵√x² with a single rational exponent

x⁶

ln 4

2 ln 2

d/dn aⁿ

ln(a) × aⁿ

d/dx log(base a)x

1/ln(a) × aⁿ

d/dx arcsin(u)

u'/√1-u²

d/dx arccos (u)

-u'/√1-u²

d/dx arctan (u)

u'/1+u²

π(x) =

R(x) - C(x)

error

actual - estimated

ln (y/x)

ln(y) - ln(x)

ln (yx)

ln(y) + ln(x)

how do you know if an object is speeding up?

acceleration and velocity have THE SAME sign

how do you know if an object is slowing down?

acceleration and velocity have OPPOSITE signs

|8x|/8x

±1

rewrite 2 ln 6 in a different form

ln 36

∫cos(x)dx

sinx + c

∫sin(x)dx

-cos(x) + c

∫sec(x)tan(x)dx

sec(x) + c

∫sec²(x)dx

tan(x) + c

∫csc(x)cot(x)dx

-csc(x) + c