Internal energies: Physical Chemistry

Internal Energy

The sum of all kinetic and potential energies in the system.

For a system of many particles, we cannot know the absolute internal energy. Only changes in internal energy matter.

Work and Heat’s effect on internal energies

Work done on a system and heat added to the system increase the internal energy of the system.

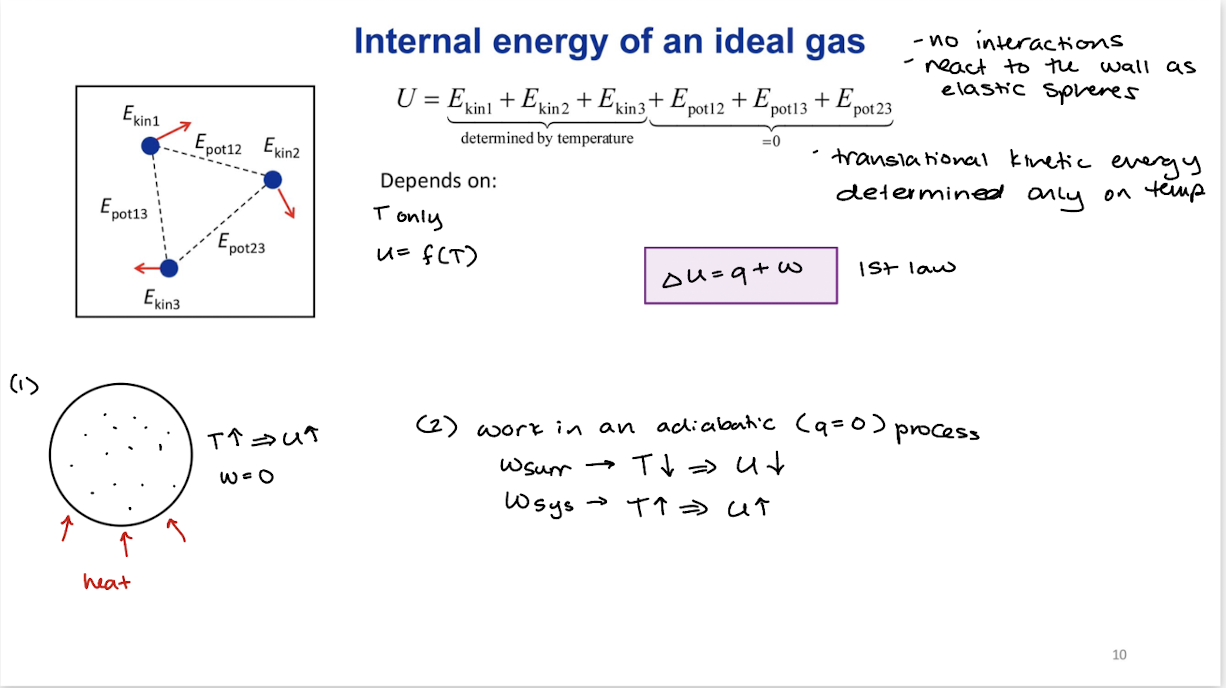
Internal energy of an ideal gas

∆U=q+w= f(T)

Depends on temperature only

Temperature effects the kinetic energy of internal molecules

Individual H₂ molecules

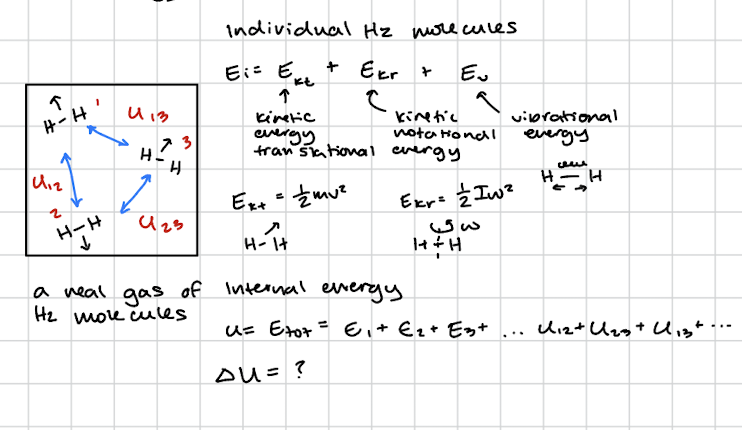
Function of Internal Energy

Internal Energy is a STATE function

∆U=q+w

Q and W are both path functions but ∆U is a state function

Internal energy vs temperature

Consider a process with constant volume (isochoric process ∆V=0)

∆U=q_v (heat added at constant V)

q_v=C_v∆T=nC_mv∆T

∆U=nC_v∆T

can be used for other T→T processes once found out because ∆U is a state function

Isochoric

Constant volume

First Law of Thermodymaics

1. First take a look at a process that occurs without heat transfer (adiabatic process)

∆U=q+w (q=0) → ∆U=w

The change of internal energy of a system in an adiabatic process equals to the work put into the system.

W_surr=-W_sys=-∆U An open cylinder getting colder releasing gas

Adiabatic expansion: w<0 and ∆U≤0: the system does work on the surroundings at the expense of its internal energy.

2. An isolated system (no work or heat transfer)

w=0 q=0 ∆U=0

The internal energy of an isolated system is constant.

We cannot extract work from the system, leaving its internal energy unchanged.

Organisms require an external supply of energy to do work as they live.

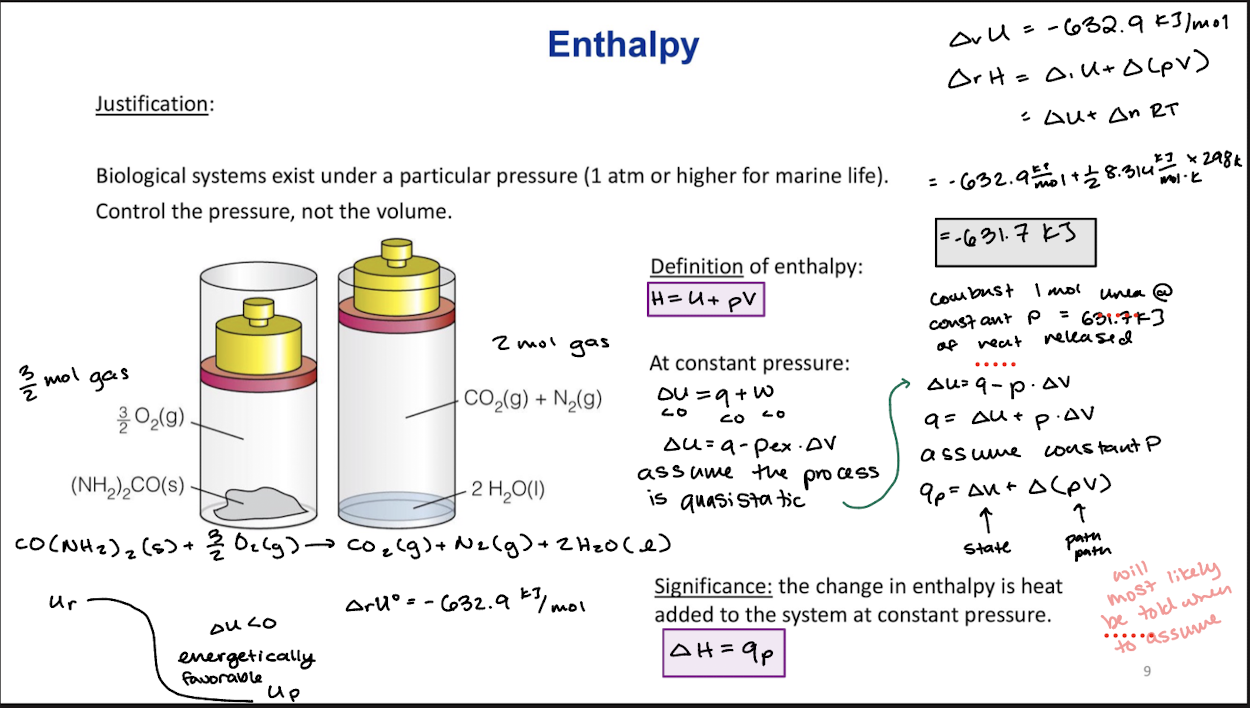
Enthalpy

Justification: Biological systems exist under a particular pressure (1 atm or higher for marine life). Control the pressure, not the volume.

H=U+pV

at constant pressure

∆U=q+w

q_p=∆U+∆(pV)

Significance: The change in enthalpy is heat added to the system at constant pressure.

∆H=q_p