Flashcards

Two lines are parallel if…

They have equal gradients

Two lines are perpendicular if…

The product of their gradients is -1

How do you calculate the distance between two points in the Cartesian plane?

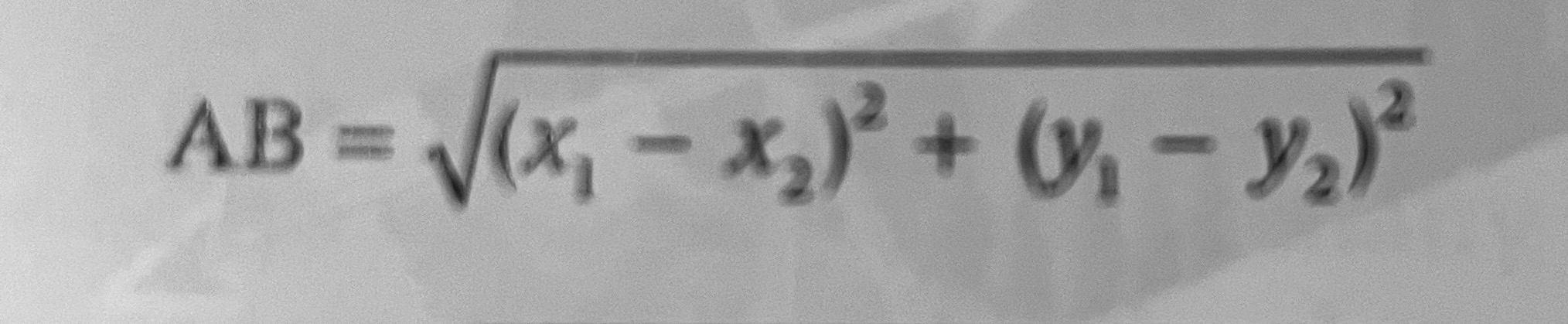
Points are collinear if…

They lie on the same line

Points or lines are coplanar if…

They lie in the same plane

What is the parallelogram law of vector addition?

In the parallelogram ABCD AB+AD=AC

What is the triangle law of vector addition?

In the triangle ABC

AB+BC=AC

Can the triangle law be used for collinear points?

Yes, unlike the parallelogram law

What is the zero vector?

A vector whose magnitude is 0 and direction is not defined/has all directions. AA=0

A vector and the vector obtained multiplying that vector by a scalar…

Have the same or opposite directions and are collinear or parallel

When are vectors collinear?

When they have directed line segments that lie on the same line

What is a position vector?

A vector that has a starting point at the origin and an end point P(x,y) at any point in the plane is a position vector of point P.

P=OP=xi+yj

What is L’Hôpital’s Rule and when is it used?

If limₓ→c f(x)/g(x) gives 0/0 or ∞/∞, then

  limₓ→c f(x)/g(x) = limₓ→c f′(x)/g′(x) (provided the limit exists)

When and how do you use logarithmic differentiation?

1. Take the natural log of both sides: ln(y) = ln(f(x)).

2. Differentiate using the chain rule.

3. Solve for y′.

Useful when the variable appears in both the base and the exponent.

What is the process for implicit differentiation?

Differentiate both sides of an equation (involving x and y) with respect to x, treating y as a function of x, then solve for dy/dx.

How do you apply the chain rule?

For a composite function y = f(g(x)), differentiate as:

  dy/dx = f′(g(x)) · g′(x).

How do you solve a separable differential equation?

For an equation dy/dx = f(x)g(y):

  1. Rewrite as dy/g(y) = f(x) dx

  2. Integrate both sides

  3. Solve for y if possible.

What does the p-test say about the series Σ1/nᵖ?

The series converges if p > 1 and diverges if p ≤ 1.

How does the ratio test work for series convergence?

For a series Σaₙ, compute L = limₙ→∞ |aₙ₊₁ / aₙ|.

  • If L < 1, the series converges.

  • If L > 1, it diverges.

  • If L = 1, the test is inconclusive.

What are the dot product and cross product of vectors?

• Dot Product: u · v = |u||v| cosθ = u₁v₁ + u₂v₂ + …

• Cross Product (in ℝ³): u × v = (u₂v₃ – u₃v₂, u₃v₁ – u₁v₃, u₁v₂ – u₂v₁)

How do you find the inverse of a 2×2 matrix?

For A = [[a, b], [c, d]] with det(A) ≠ 0,

  A⁻¹ = (1/(ad – bc)) · [[d, –b], [–c, a]].

How do you multiply matrices and find the determinant of a 2×2 matrix?

• Multiplication: For A (m×n) and B (n×p), (AB)_ij = Σ (A_ik · B_kj).

• 2×2 Determinant: For A = [[a, b], [c, d]], det(A) = ad – bc.

What is the integration by parts formula and a tip for choosing parts?

• Formula: ∫ u dv = uv – ∫ v du

• Tip: Use the LIATE rule (Logarithmic, Inverse trig, Algebraic, Trigonometric, Exponential) to choose u and dv.

How do you perform integration by substitution?

1. Choose u = g(x) so that its derivative du = g′(x) dx appears in the integrand.

2. Rewrite the integral in terms of u, integrate, and then substitute back.

What are the derivatives of arcsin(x) and arctan(x)?

• d/dx [arcsin(x)] = 1/√(1 – x²) (for |x| < 1)

• d/dx [arctan(x)] = 1/(1 + x²)

What is the Binomial Theorem for expanding (a + b)ⁿ?

(a + b)ⁿ = Σₖ₌₀ⁿ (n choose k) a^(n–k) bᵏ, where (n choose k) = n!/(k!(n–k)!).

What is De Moivre’s Theorem?

For any integer n,

  [r (cosθ + i sinθ)]ⁿ = rⁿ [cos(nθ) + i sin(nθ)].

It’s used to compute powers and extract roots of complex numbers.

How can a complex number be expressed in polar and exponential forms?

• Polar Form: z = r (cosθ + i sinθ), where r = |z| and θ is the argument.

• Exponential Form: z = r·e^(iθ).

How do you find the modulus and argument of z = a + bi?

• Modulus: |z| = √(a² + b²)

• Argument (θ): θ is found by solving cosθ = a/|z| and sinθ = b/|z| (keeping in mind the quadrant of z).

What is the standard form of a complex number?

A complex number is written as a + bi, where a is the real part, b is the imaginary part, and i = √(–1).