set theory and logic

Axioms of partial ordering

Reflexivity

Antisymmetry

Transitivity

defenition of a partial ordering (poset)

A relation ⊆ on a set A is called a partial ordering if the following properties are satisfied for all a,b and c in A

• Reflexivity: a ⊆ a

• Antisymmetry: If a ⊆ b and b ⊆ a, then a = b

• Transitivity: if a ⊆ b and b ⊆ c, then a ⊆ c

What’s the distinction between partial and total ordering

In total ordering all elements are comparable with each other, in partial ordering this is not necessary

Condition of reflexivity

a is ranked less than or equal to a

Condition of Antisymmetry

If a is ranked less than or equal to b and b is ranked less than or equal to a then a = b

Condition of transitivity

If a is ranked less than or equal to b and b is ranked less than or equal to c, then a must be ranked less than or equal to c

How can this be read

a is ranked strictly below b

additional condition for a relation on set A to be a totally ordered set

Comparability: either a ⊆ b or b ⊆ a is true

(every element is ranked against every other element)

give an example of when reflexivity is not true

take Z, it is true that 1 = 1. Now take the relation ⊆ to be <. Then clearly 1 ⪯̸ 1 so this natural-looking relation is not reflexive

Poset

A partially ordered set

what is the power set of S where S = {1,2}

P(S) = {∅, {1}, {2}, {1,2}}

Draw a Hasse diagram for the power set of S = {1,2} using the subset ordering

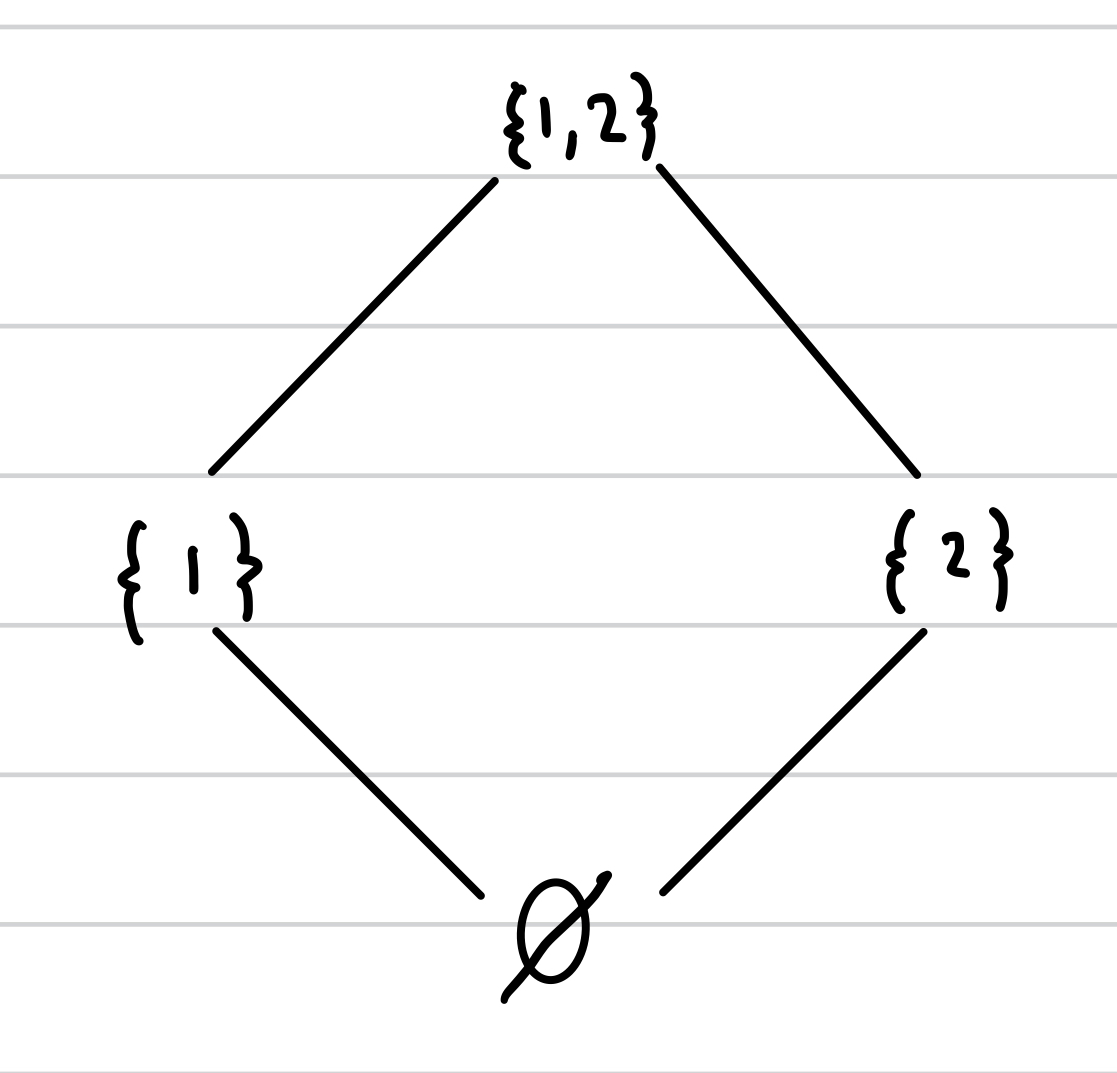
How does subset ordering work

a ⊆ b if every element of a is also an element of b

What is the additional axiom of total ordering

Comparability (totality)

Condition of comparability

For all a and b in A, either a is ranked less than or equal to b or b is ranked less than or equal to a

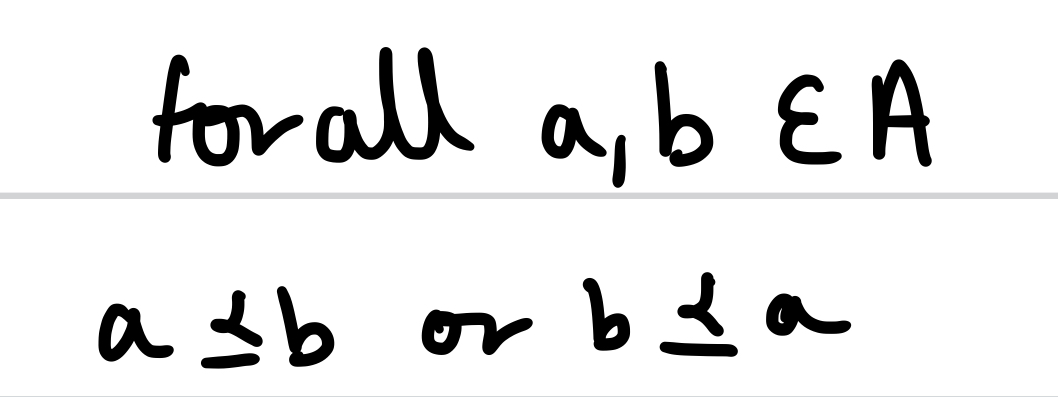
What is the relationship between partially ordered sets and totally ordered sets

Every totally ordered set is also a poset but not every poset is a totally ordered set

Maximal element

An element, m, of a poset, P, such that there is no element x in P where m is ranked strictly less that x. Therefore, either x is ranked less than or equal to m or m is not ranked with x

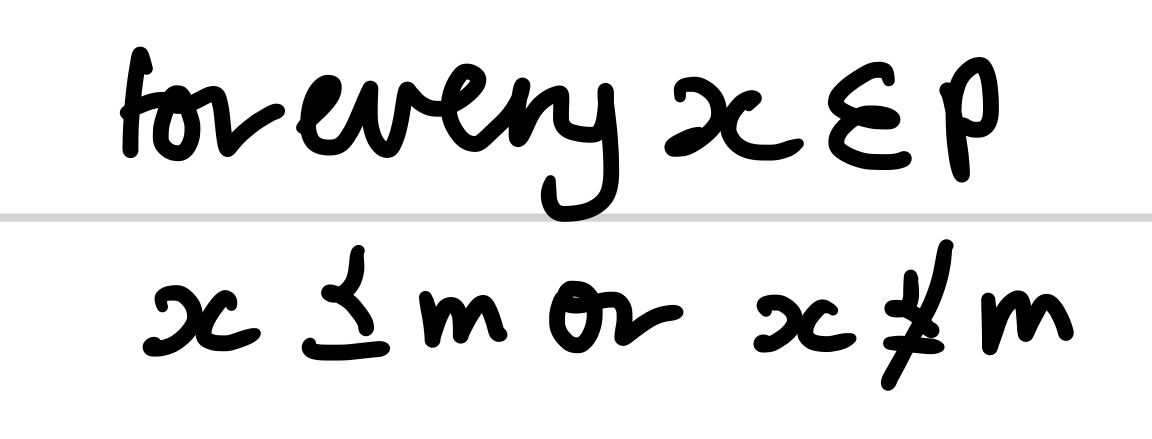
3 conditions for the greatest element

1. g is an element of S

2. For every element s ∈ S, s is ranked less than or equal to g

3. No other element in S satisfies the above two properties simultaneously

which are the maximal element(s) in the poset P = {∅, {1}, {2}, {3}, {1,2}} ordered by the subset relation ⊆

{1,2} and {3}

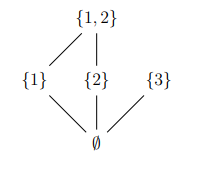
Relationship between greatest and maximal element

A greatest element will always also be a maximal

Hasse diagram for S = {1, 2, 3, 4, 5, 6} where a is ranked less than or equal to b if a divides b

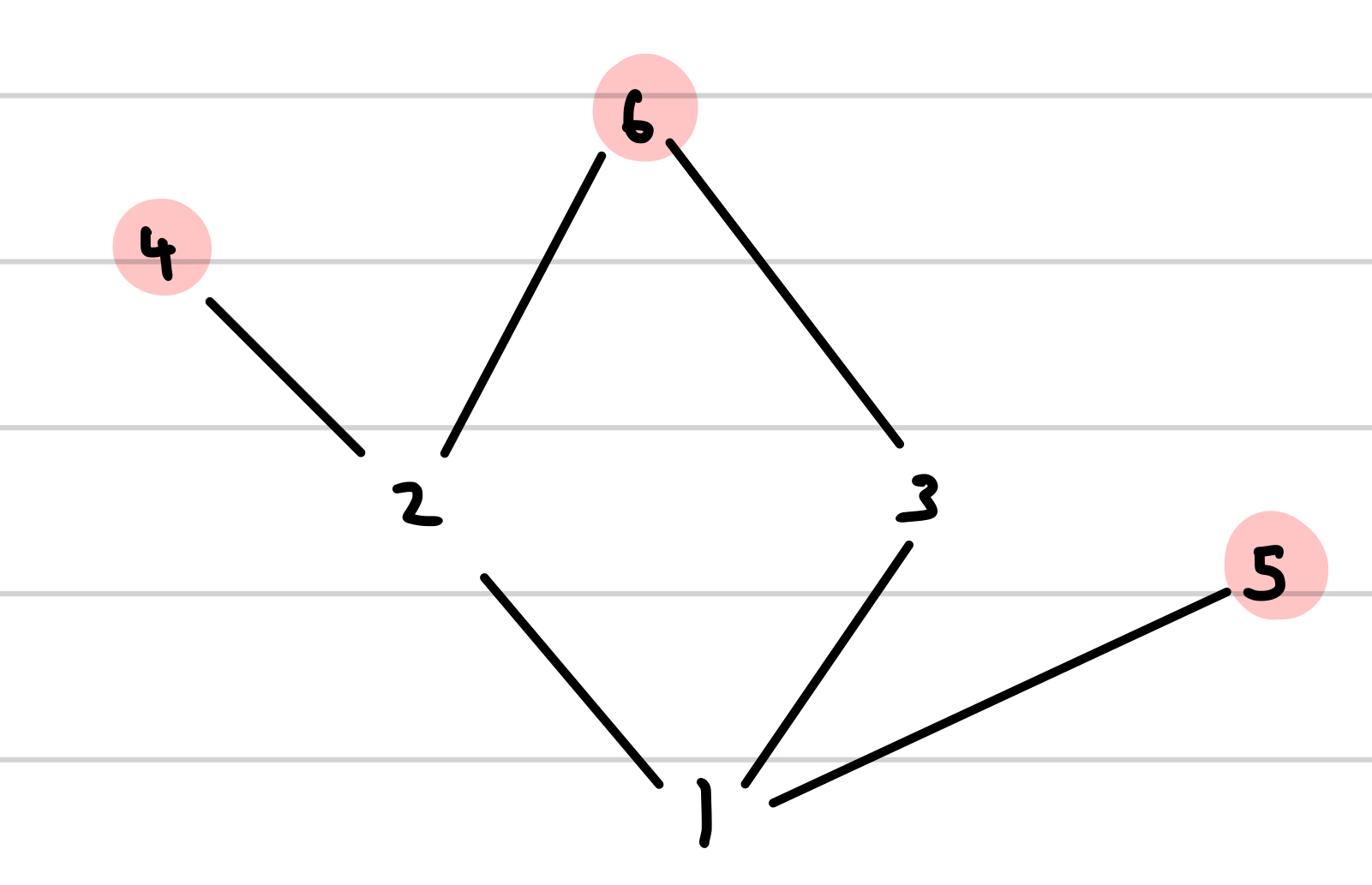
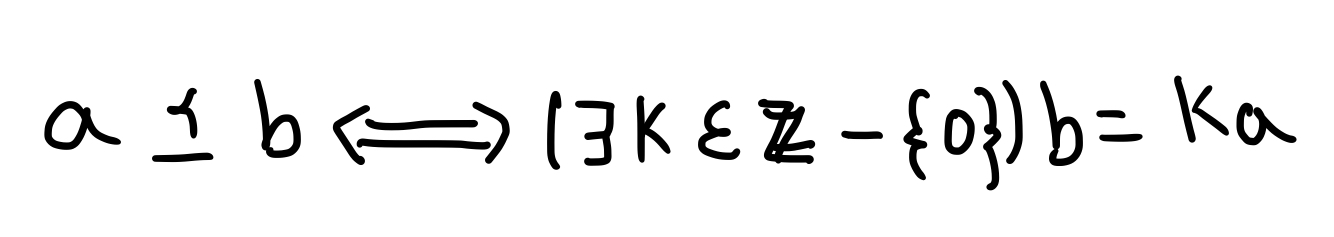
Meaning of

a is ranked less than or equal to b if and only if there exists an integer excluding zero, k, such that b = ka

How can a maximum element not exist

Poset (N, <)

The infinite set of natural numbers

construct a poset that has exactly 1 maximal element 

for the only maximal element to not be the greatest element, the poset must be infinite, eg take ≤ on the set of positive integers and let 1≤2, then 2 becomes a maximal element but not greatest 

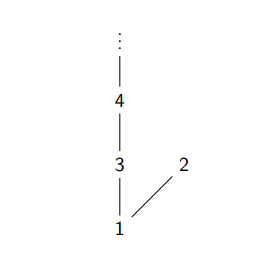
Proof that every nonempty finite set has at least 1 maximal element

Proof by contradiction

Assume that A is a nonempty finite poset of size n with no maximal element. Take element a₁ ∈ A. Then ∃ a₂ ∈A such that a₁ ≤ a₂

continue in this way until reaching aₙ

a₁ ≤ a₂ ≤ a₃ …≤ aₙ

But aₙ cannot be maximal either, so ∃ aₙ₊₁ such that aₙ ≤ aₙ₊₁

Contradiction as n+1 distinct elements found, thereby A must have at least one maximal element

What can be said about a totally ordered finite poset

Must have a greatest element

N

Natural numbers = {1, 2, 3, …}

Z

Integers = {…-3, -2, -1, 0, 1, 2, 3, …}

Q

rational numbers = {p/q: p ∈ Z ∧ q ∈ Z - {0}}

A → B

A implies B

if A, then B

A is a sufficient condition for B

B is a necessary condition for A

what is a sufficient condition

something that guarantees a result

eg being divisible by 4 is a sufficient condition to be an even number

A ← B

A is implied by B

if B, then A

A is a necessary condition for B

B is a sufficient condition for A

P: Paul is happy

Q: Paul paints a picture

Sentence: “Paul is happy only if he paints a picture.”

P → Q

P: Paul is happy

Q: Paul paints a picture

Sentence: “If Paul is happy, then he paints a picture.”

P → Q

for A → B construct the inverse

¬A → ¬B

for A → B construct the contrapositive

¬B → ¬A

for A → B construct the converse

B → A

Which type of logical statement is equivilent to the original

Contrapositive

Prove (∀a, b ∈ Z)(a + b ≥ 15 ⇒ a ≥ 8 ∨ b ≥ 8)

Use proof by contraposition

contrapositive: (∀a, b ∈ Z)(a < 8 ∧ b < 8 ⇒ a + b < 15)

a < 8 ∧ b < 8 ⇒ a ≤ 7 ∧ b ≤ 7 ⇒ a + b ≤ 14 < 15

The contrapositive statement is true. We have proved the original statement is true using proof by contraposition

∀

for all

∃

there exists

difference between

(∀x)(∃y) x > y

(∃y)(∀x) x > y

For every x there is a y such that x > y

vs

there is a y such that for every x, x > y

Negate (∀x ∈ R)P(x),

(∃x ∈ R)¬P(x)

Prove (∀n ∈ Z)n² is even ⇒ n is even

Proof by contradiction

assume the negation: (∃n ∈ Z)n² is even → n is odd

((∃n ∈ Z)n² is even ⇒ n is odd) ↔ (∃a, b ∈ Z)(2a + 1)² = 2b

(2a + 1)² = 2b

4a² + 4a + 1 = 2b

2a² + 2a + ½ = b

½ = b − 2a² − 2a

contradiction as RHS is an integer, but LHS is not