Algorithms Midterm 1

COP 4531 - Algorithm Design & Analysis

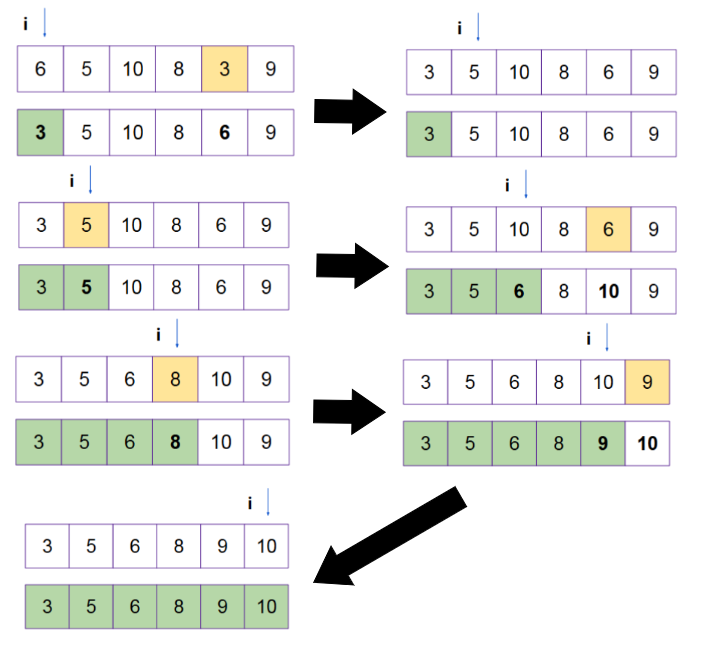
Selection Sort

1. Scan the entire array and find the smallest element

2. Swap the smallest element with the element at index i

3. Increment i

4. Repeat for the rest till i = 6

Step 1: n operations, Step 2: n-1 operations, Step 3: n-2 operations → n(n+1)/2

Run time complexity = O(n²)

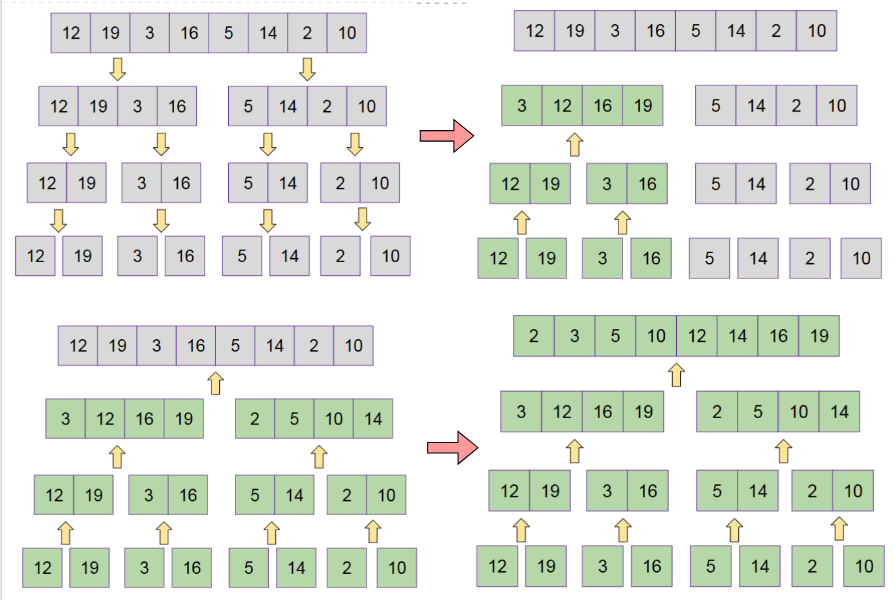
Merge Sort (Divide and Conquer)

1. Break down the array, sort each part.

2. Merge the pieces back together.

n operations for each subproblem (n → n/2 → n/4 … 1)

Run time complexity = O(nlogn)

Recurrence Relation: T(n) = 2T(n/2) + O(n)

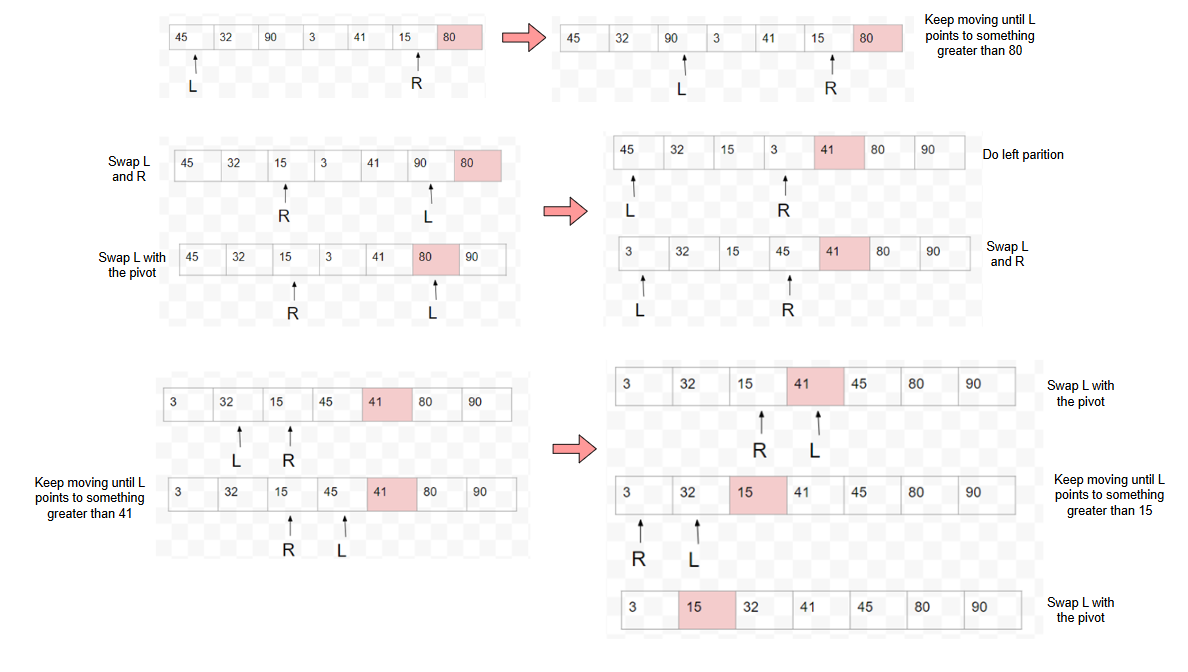
Quick Sort (Divide and Conquer)

1. Select a pivot randomly. → O(1)

2. Partition the array around the pivot: compare, swap. → O(n)

3. Rules: Left pointer should always point to element smaller than pivot. Right pointer should always point to element larger than pivot.

**Partitioning places all the elements less than the pivot in the left part of the array, and all elements greater than the pivot in the right part of the array.

n steps total, each comparison is n-1 → n(n-1)

Worst Case (when pivot not in middle): O(n²)

Best + Average Case: O(nlogn)

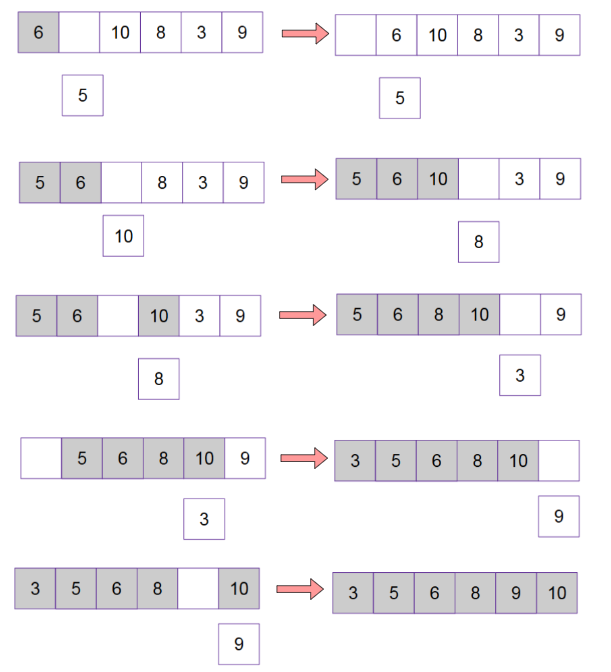
Insertion Sort

1. Insert each element into a sorted partition.

2. Pull the first element out of the unsorted partition of the array.

3. Compare with the sorted array.

4. Shift to empty spot on the right if larger.

Number of operations: 1 + 2 + 3 + … + n-1= n(n-1)/2

Run time complexity = O(n²)

Integer Multiplication (Divide and Conquer)

Recurrence relation: T(n) = 3T(n/2) + cn

Time complexity: O(n^1.59)

Matrix Multiplication (Divide and Conquer)

Reduces the number of multiplications and additions/subtractions to 7 and 18

Recurrence relation: T(n) = 7T(n/2) + O(n²)

Time complexity: O(n^2.81)

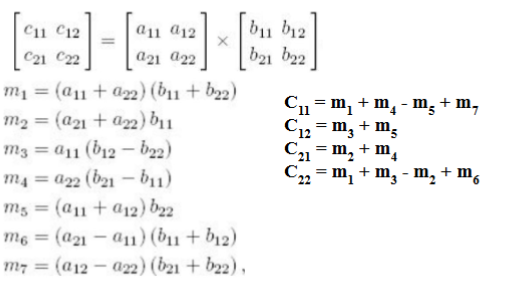
Closest Pair (Divide and Conquer)

1. Divide the 2D space into 2 regions such that the number of points in the regions are roughly the same

2. Find the closest pair in the left and right region → T(n/2)

3. Check if there exists a pair such that one pair is in the left and other is in the right and the distance between them is lesser than min {d₁,d₂}

Recurrence relation: T(n) = 2T(n/2) + O(n)

Time complexity: O(nlogn)

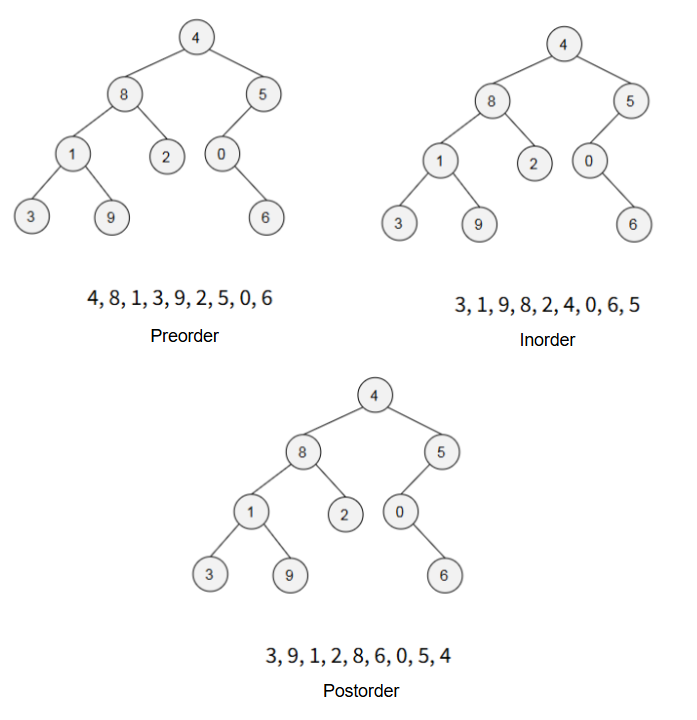
Binary Tree Traversal

• Preorder → root, left, right

• Inorder → left, root, right

• Postorder → left, right, root

# Example of Preorder
void preorder (Node *p){
   if(p != NULL){
       cout << p->data << endl;
       preorder(p->left_child);
       preorder(p->right_child);
   }
}

Binary Search Tree

• For each node p, all the values stored in the left subtree of p are LESS than the value stored in p.

• All the values stored in the right subtree of p are GREATER than the value stored in p.

• Normally, if we search through n nodes, it takes O(n)

• But using binary search tree:

  • We choose to look to the left OR look to the right of a node

  • We are HALVING the search space

  • Time complexity: O(logn)

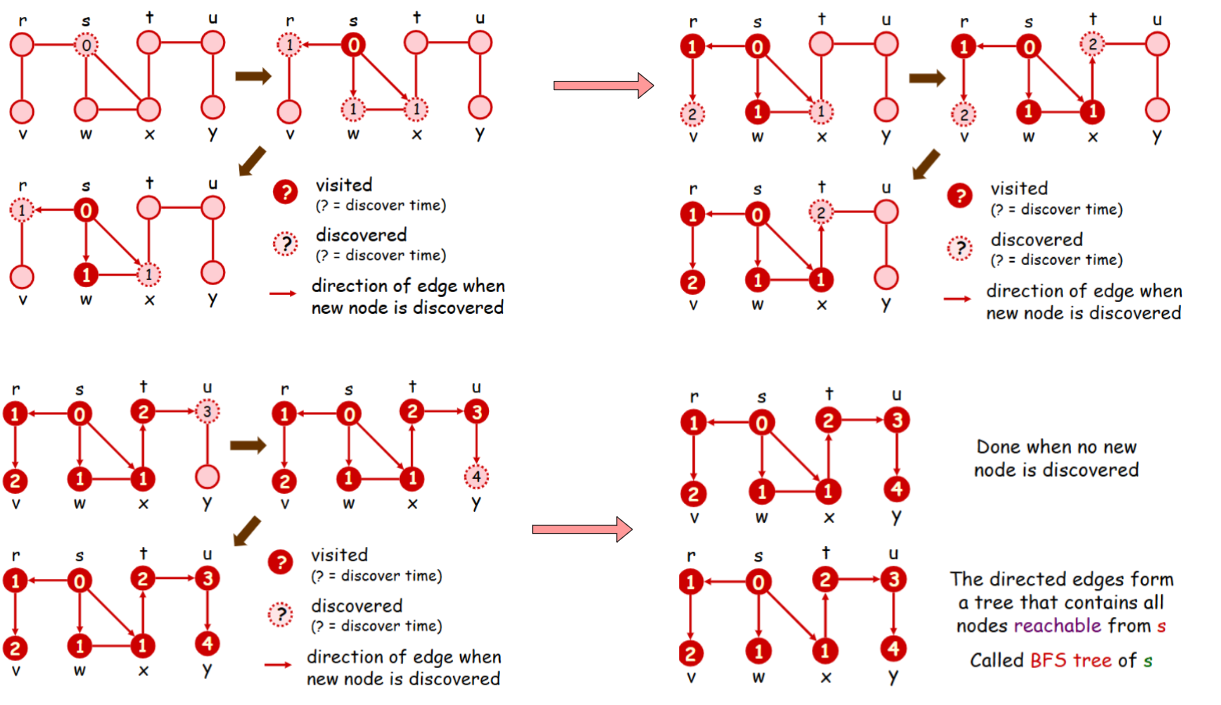
Breadth First Search (BFS)

1. Enqueue the given source vertex into a queue and mark it as visited.

2. While the queue is not empty:

   • Dequeue a node from the queue and visit it.

   • For each unvisited neighbor of the dequeued node:

     • Enqueue the neighbor into the queue.

     • Mark the neighbor as visited.

3. Repeat step 2 until the queue is empty.

Total time and space: O(|V|+|E|)

Depth First Search (DFS)

1. Push the given source vertex into a stack and mark it as visited.

2. For each unvisited neighbor, add it to stack, mark it as visited, and explore its neighbors. If it has no neighbors, pop it from stack.

3. Repeat step 2 until stack is empty.

Total time: O(|V|+|E|)

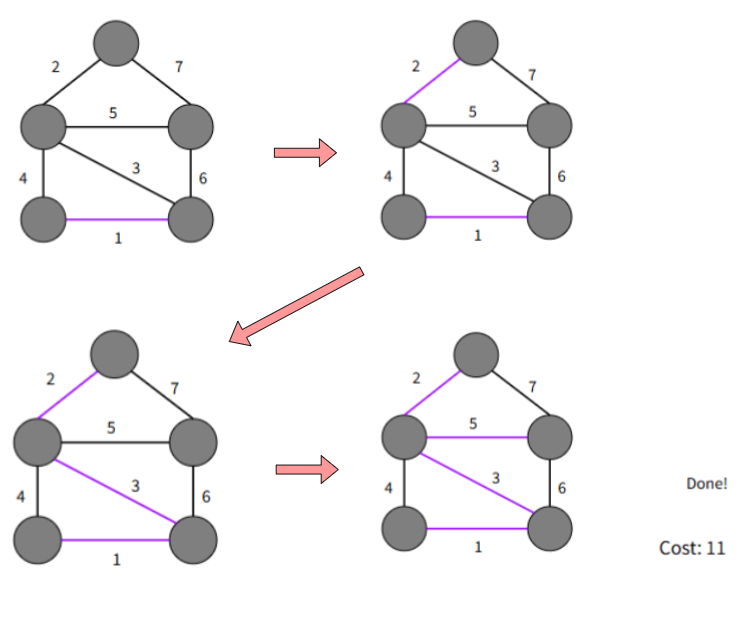
Kruskal Greedy Algorithm

1. Sort the graph edges with respect to their weights.

2. Start adding edges to the MST from the edge with the smallest weight until the edge of the largest weight.

3. Only add edges which doesn't form a cycle.

Time complexity: O(|E|log|E|)

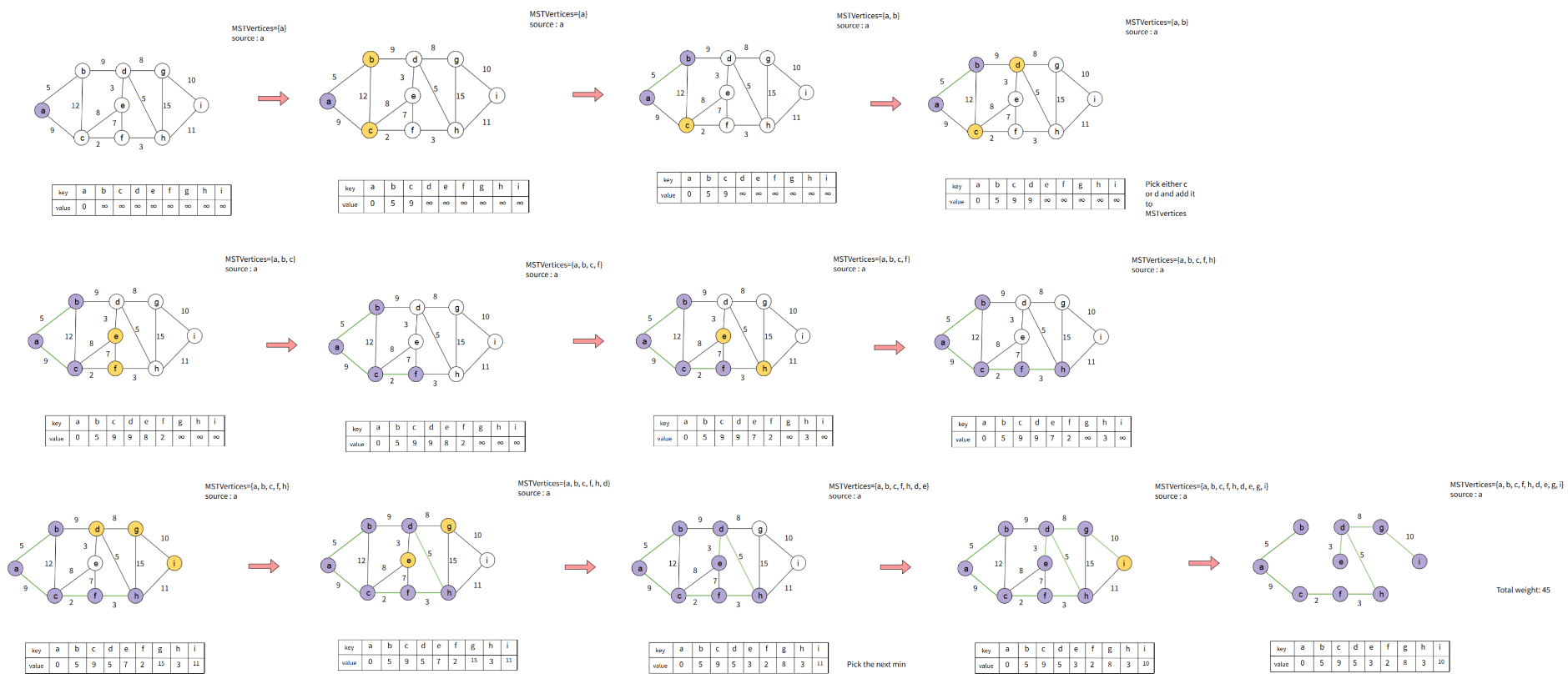
Prim Greedy Algorithm

1. Create an empty spanning tree. The idea is to maintain two sets of vertices. The first set contains the vertices already included in the MST, and the other set contains the vertices not yet included.

2. At every step, it considers all the edges that connect the two sets and picks the minimum weight edge from these edges.

3. After picking the edge, it moves the other endpoint of the edge to the set containing MST.

Implemented using Binary Heap/Priority Queue

Time Complexity: O(ElogV)

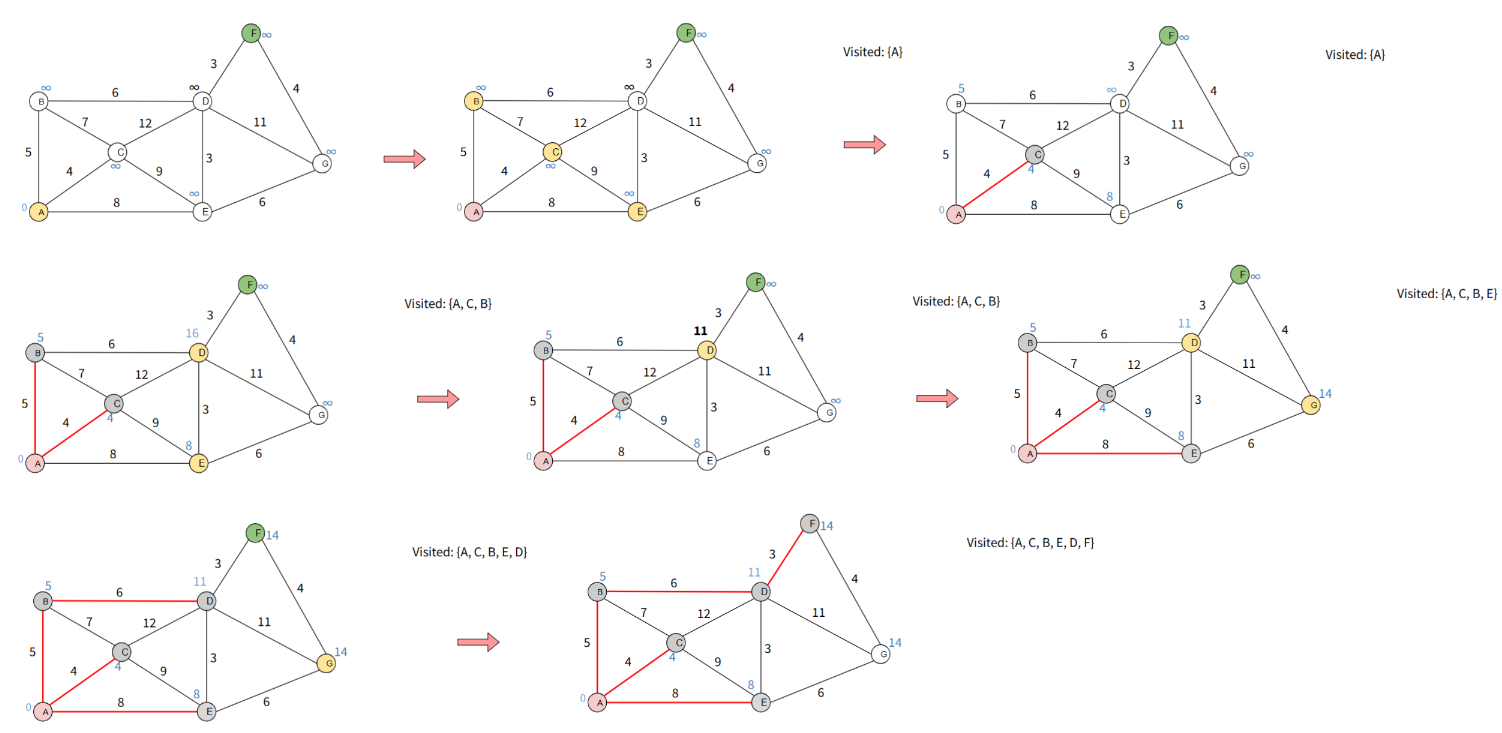
Dijkstra Greedy Algorithm (Shortest Path)

1. Assign 0 to source and infinity to all other nodes

2. Keep a set of visited nodes

3. For the current node consider all of its unvisited neighbors and calculate “distance to the current node” + “ distance from current node to the neighbor”. If it is better, update the value (relaxation step)

4. When we are done considering all neighbors of the current node, mark current node as visited

5. If the goal node is visited, we are done

6. Set the unvisited node marked with the smallest value as the next current node and repeat step 3

Time complexity: O((|E|+|V|) log v)

Recurrence Relation

1. Do some substitution until the pattern emerges

2. Find the general form in terms of k

3. Remove k

4. Find the closed formula in terms of n

5. Find the dominating term

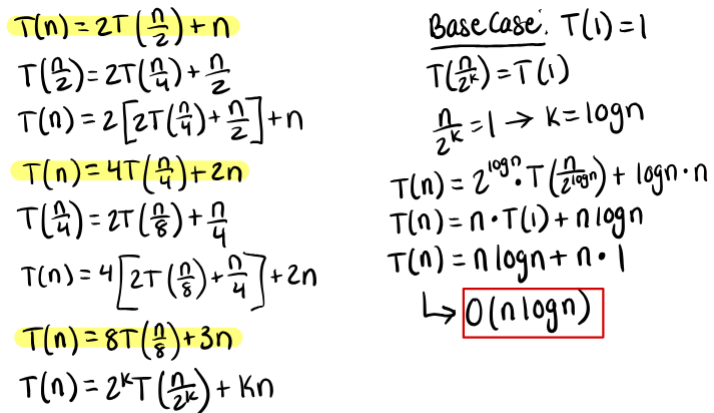
Find the time complexity for the following:

int count = 0;
for (int i = 0; i <= n; i++)
  for(int j = 1; j <= n; j++)
    count++;

There are two nested for loops. Each of them runs n times.

Time complexity: O(n²)

Find the time complexity for the following:

int count = 0;
for (int i = 1; i <= n; i++)
  for(int j = 1; j <= i; j++)
    count++;

Inner loop relies on outer loop. When i = 1, we have one execution. When i = 2, we have two executions and so on. In total: 1 + 2 + 3 + … + n = n(n+1)/2

Time complexity: O(n²)

Find the time complexity for the following:

int count = 0;
for (int i = 1; i <= n; i = i*2)
  for(int j = 1; j <= n; j++)
    count++;

Inner loop runs n times, outer loop runs log n times since at each step we are doubling i (1, 2, 4, 8, …, n).

2^k = n → k = log n

Time complexity: O(nlogn)

Find the time complexity for the following:

int count = 0;
for (int i = 1; i <= n; i = i*2)
  for(int j = 1; j <= i; j++)
    count++;

When i = 1, the whole code runs 1 time. When i = 2, it runs 2 times. When i = 4, it runs 4 times and so on. In total, we have 1 + 2 + 4 + … + 2^k where k is log n because of outer loop.

(2^logn+1 - 1)/(2 - 1) → 2^logn+1 = n + 1

Time complexity = O(n)

Analyze the running time complexity of the following function which finds the kth smallest integer in an unordered array.

int selectkth(int a[], int k, int n){
    int i, j, mini, tmp;
    for (i = 0; i < k; i++)
        mini = i;
        for (j = i+1; j < n; j++)
            if (a[j] < a[mini])
               mini = j;
        tmp = a[i];
        a[i] = a [mini];
        a[mini] = tmp;
    }
    return a[k-1];
}

If we assume that the input array is always sorted, how can we rewrite the above function to return the kth smallest element of the sorted array? What would be the running time complexity in that case?

1. (n - 1) + (n - 2) + … + (n - k) = (2n - k - 1)k/2 = O(n²) (worst case: k = n)

2. Just return a[k-1] and time complexity would be O(n)

Recursive Binary Search Pseudocode

function BST(array, low, high, x){
   if (low > high)
      return -1
   mid = (low + high) / 2
   if (x == array[mid])
      return mid
   else if (x < array[mid])
      return BST(array, mid+1, high, x)
   else 
      return BST(array, low, mid-1, x)
}

Recurrence Relation: T(n) = T(n/2) + 1

You are given three arrays of different sizes, each array is sorted in ascending order. Merge all the arrays into one sorted array and return the final array. Write the pseudocode with linear time complexity.

function merge(X, Y)
    Let m and n be the sizes of X and Y.
    Let T be the array to store result
    // Merge by taking smaller element from X and Y
   while i < m and j < n
       if X[i] <= Y[j]
          Add X[i] to T and increment i by 1
       else Add B[j] to T and increment j by 1
   while j < n
       Add B[j] to T and increment j by 1
   while i < n
      Add X[j] to T and increment i by 1
   Return T

function merge_three_array(A, B, C)
   R = merge(A, B)
   return merge(R, C)

You are given a set of n points on a 2D plane, where each point is represented as a pair of coordinates (x,y). Our task is to design an algorithm that finds the closest pair of points. The distance between two points (x₁, y₁) and (x₂, y₂) is given by the Euclidean distance formula. Design an efficient algorithm to solve this problem using the Divide and Conquer approach.

def closestPair(P[], Q[]):
    # Base Case: If the number of points is <= 3, use brute-force to find the closest pair.
    if len(P) <= 3:
       return bruteForce(P)

    # Divide: Find the middle point
    mid = len(P) // 2
    midpoint = P[mid]

    # Divide the points into two halves
    P_left = P[:mid]
    P_right = P[mid:]

    # Conquer: Find closest pairs in both halves
    d_left = closestPair(P_left, Q)
    d_right = closestPair(P_right, Q)

    # Minimum distance so far
    d_min = min(d_left, d_right)

    # Combine: Check for points across the divide within d_min distance
    strip = [p for p in Q if abs(p.x - midpoint.x) < d_min]
   
    # Check the strip for a closer pair (only within the next 6 points in the y-sorted strip)
    d_strip = stripClosest(strip, d_min)
    return min(d_min, d_strip)

def stripClosest(strip, d_min):
    min_dist = d_min
    # For each point in the strip, check the next 7 points
    for i in range(len(strip)):
       for j in range(i + 1, min(i + 7, len(strip))):
            if distance(strip[i], strip[j]) < min_dist:
                 min_dist = distance(strip[i], strip[j])
     return min_dist

Sorting: O(nlogn)

Recursive Calls: T(n) = 2T(n/2) + O(n)

Time complexity: O(nlogn)

Which order is correct for the following runtime complexity functions from smallest to largest?

1. n < log n < n^2 < n logn < 2^n

2. log n < n < n logn < 2^n < n^2

3.  n < n logn < n^2 < log n < 2^n

4. log n < n < n logn < n^2 < 2^n

4. log n < n < n logn < n^2 < 2^n

What is the run-time complexity of the following program segment?

for ( int i = 1; i <= 100; i++)
        cout << i << endl;

Constant → O(1)

What is the run-time complexity of the following program segment?

for (int i = 1; i <= n; i = i *4)
        cout << i << endl;

O(logn)

Express the following runtime complexity function using big O notation: T(n) = 50log n+ 100n³ + 200n²

O(n³)

Express the following runtime complexity function using big O notation: T(n) = n + 4 log n + 42

O(n)

What is the run-time complexity of the following program segment?

for(int i = 1; i <= n; i++)
        for(int j = 0; j < n; j++)
                for (int k = 0; k < n; k++)
                        cout << i * j << endl;

O(n³)

What is the run-time complexity of the following program segment?

for(int i = 1; i <= n; i = i*2)
        for(int j = 0; j < n; j+=2)
                cout << i * j << endl;

O(n logn)

What's the worst-case runtime complexity for the following function?

int foo(int n)
{
        int product = 1;
        for (int i = 2; i < n; i++)
                for (int j = 0; j < n; j++)
                        product = product * j;

         return product;

}

O(n²)

What's the best-case runtime complexity for the following function?

int foo(int n)
{
        int product = 1;
        for (int i = 2; i < n; i++)
                for (int j = 0; j < n; j++)
                        product = product * j;

         return product;

}

Note: We have to assume n is arbitrarily large. We cannot just assume n = 0 or n = 1.

O(n²)

Which are the following statements are true? You can select more than 1 choice. 

1. n² = O(n)

2. m³ = O(2^m)

3. 3 = O(log k)

4. n + nlog n = O(n)

5. 2150 = O (1)

6. logm + 100 m logm = O(mlog m)

7. n^2.8 = O(n²)

2. m³ = O(2^m)

3. 3 = O(log k)

5. 2150 = O (1)

6. logm + 100 m logm = O(mlog m)

Which one of the following algorithms does not certainly divide the input size by two when the divide and conquer approach is applied?

1. Closest Pair

2. Quick Sort

3. Binary Search

4. Merge Sort

2. Quick Sort

Which traversal algorithm is the following?

void traverseTree(Node node)
{
         if (node == null)
                   return;
 cout<< node-> data ;
 traverseTree (node->left);
 traverseTree (node>right);
}

Pre-order traversal algorithm

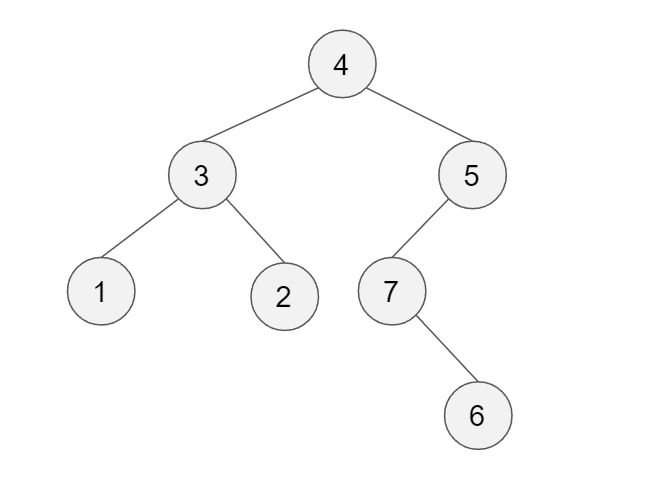
The tree on the left is given, which of the following is in-order traversal of the tree? 

1, 3, 2, 4, 7, 6, 5

Which of the following statements are true on an array of size n? Select all possible answers.

1. Merge Sort has worst case time of O(nlog n)

2. Quick Sort has best case time of O(nlog n)

3. Merge sort has worst case time of O(n²)

4. Merge sort has average case time of O(nlog n)

5. Quick sort has worst case time of O(nlog n)

6. Insertion sort has worst case time of O(n²)

7. Selection sort has worst case time of O(nlog n)

1. Merge Sort has worst case time of O(nlog n)

2. Quick Sort has best case time of O(nlog n)

4. Merge sort has average case time of O(nlog n)

6. Insertion sort has worst case time of O(n²)

Given a tree, assume you want to visit some vertices. You start from the root and then, you explore as far as possible along each branch before backtracking. Which algorithm is this?

Depth First Search

Which Graph Traversal Algorithm is Better?

It Depends on the Situation.