Physical Chemistry (I. Quantum Mechanics)

Contains necessary topics to be memorized for general physical chemistry.

Blackbody Radiation

The thermal radiation emitted by a perfect blackbody, which absorbs all incident radiation, is characterized by a spectrum that depends solely on its temperature, described by Planck's law.

Rayleigh-Jeans Law

An early model for blackbody radiation, proposing that energy density is proportional to the square of the frequency of the radiation, which fails at short wavelengths. It predicted that a blackbody would emit infinite energy at short wavelengths, but experiments showed this was incorrect.

Ultraviolet Catastrophe

The phenomenon wherein classical physics predicts an infinite amount of emitted energy from a blackbody at ultraviolet wavelengths, contradicting experimental observations and leading to the development of quantum mechanics.

Blackbody Quantization Formula

E=nhv

Wave-Particle Duality

Electron exhibits particle and wave-like properties by de Broglie.

de Broglie Equation

λ= h/p = h/mv

Double Slit Experiment

Shows the wave-particle duality of light. (1) As a wave: when particles pass through the double slits, each acts like a wave and interferes with itself, producing an INTERFERENCE PATTERN; (2) As a particle: when a DETECTOR is used to determine which slit the particle goes through, the interference pattern vanishes, and TWO SEPARATE BANDS appear.

6 Postulates of Quantum Mechanics

1. Wavefunction

2. Hermitian Operators

3. Eigenvalues

4. Expectation Values

5. Time-dependent Schrodinger Equation

6. Pauli-Exclusion Principle

Criteria for acceptable wavefunction (4)

1. Continuous and Continuously differentiable

2. Single-valued and finite

3. Square-integrable

4. Can be normalized

Hermitian Operators

Operators that represent measurable quantities, hence, their eigenvalues are always real numbers.

NOTE: When two Hermitian Operators commute (AB=BA), they can have a common set of eigenfunctions and both observables can be measured at the same time.

Momentum (Px) formula

The formula for momentum in quantum mechanics, represented by:

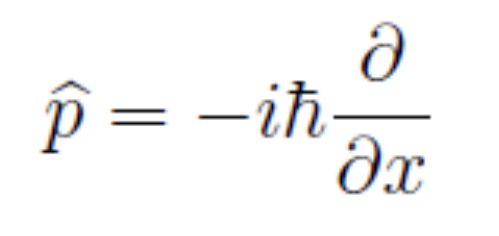
Potential Energy Operator (V)