Unit 2 - Differentiation: Definition and Basic Derivative Rules

Flashcards for AP Calculus Unit 2

What does a derivative represent?

The instantaneous rate of change of a function; the slope of the tangent line

Average rate of change

Slope of the secant line over an interval

Instantaneous rate of change

Slope of the tangent line at a point

Difference between average and instantaneous rate of change

Average uses two points (secant); instantaneous uses one point (tangent)

Formal definition of derivative

Formal (h → 0) focuses on a small change h

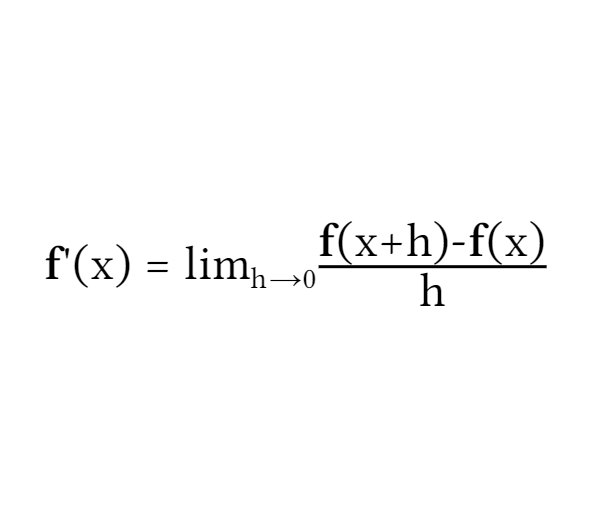
Alternate definition of derivative

Finds the exact value of the derivative evaluated at one exact point

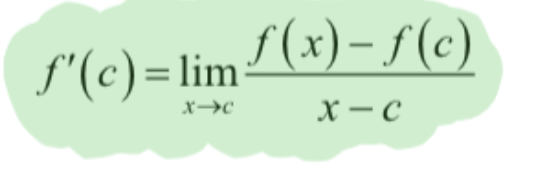
When must you use the definition of the derivative

When rules are not allowed or when explicitly asked

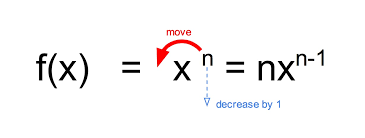
Power rule

Derivative of a constant

0

Constant multiple rule

Sum rule/Difference Rule

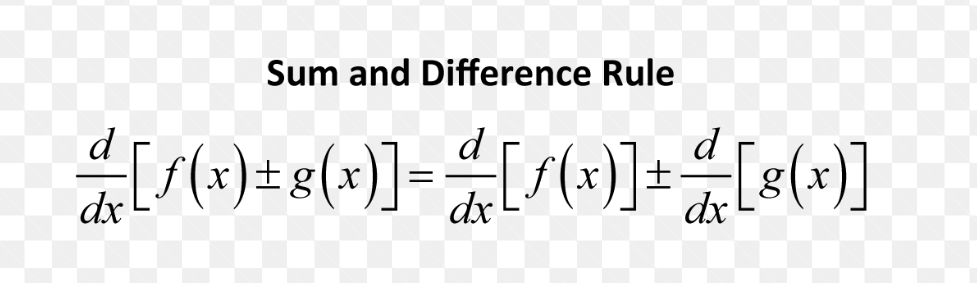
Derivative of x

1

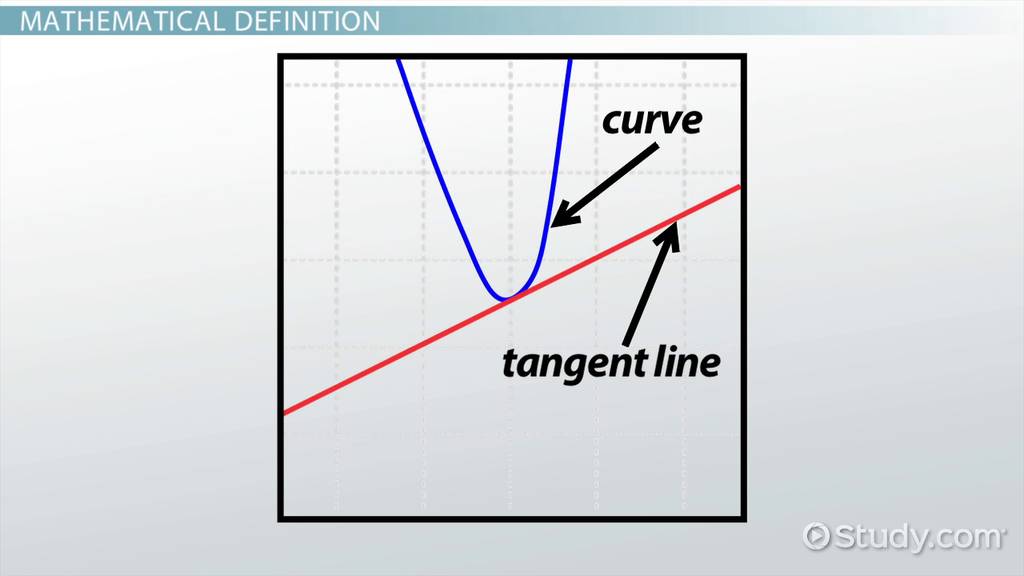
Tangent line

A line that touches the curve at one point and has the same slope there

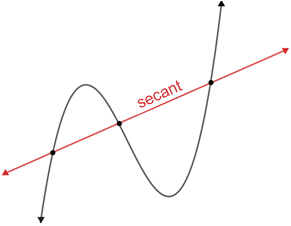
Secant line

A line that intersects a curve at two points

Difference between tangent and secant line

Tangent touches once; secant crosses twice

Equation of tangent line at x=a

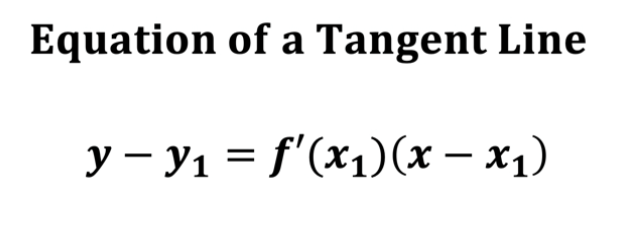
Position function

s(t) gives location as a function of time

Velocity

Derivative of position with respect to time

Acceleration

Derivative of velocity with respect to time

Positive velocity

Object moving in the positive direction

Negative velocity

Object moving in the negative direction

Velocity equals zero

Object is momentarily at rest

Acceleration equals zero

Velocity is not changing

Meaning of f(a)

The output (y-value) of the function at x=a

Meaning of f'(a)

The slope of the tangent line at x=a

Meaning of f'(a) in words

Instantaneous rate of change at x=a