MO 6,7 Nad określone układy lin. rów. alge.

Postać nad określonego układu równań lin., liniowe zadanie najmniejszych kwadratów

Ax = b

A_{m x n} - (gdzie m > n = rank(A)) mac. nie kwadratowa

Więcej równań niż niewiadomych.
Układu nie da się ściśle rozwiązać

Wektor rezidualny

r = b - Ax = 0

Wektor mówi nam jak bardzo nasze przybliżone rozwiązanie spełnia układ równań.

Szukanie najlepszego rozwiązania x^

Takie, że
|| r || = || b - Ax || = min

Jeśli zastosujemy normę 2 || r ||₂

to mamy LINIOWE ZADANIE NAJMNIEJSZYCH KWADRATÓW

x - pseudo rozwiązanie

Rozwiązanie zadania najmniejszych kwadratów

Rozwiązaniem zadania najmniejszych kwadratów jest wektor x spełniający

tzw. układ równań NORMALNYCH (prostopadłych do siebie)

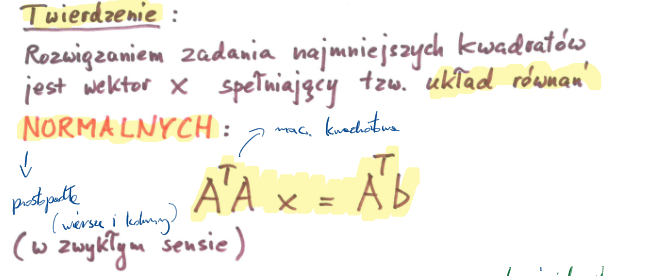
Dowód metody najmniejszych kwadratów

Rozwiązanie w praktyce metodą najmniejszych kwadratów

1. Przekształcamy do postaci Ax - b = 0

2. Liczymy 2 normę z układu równań

3. Liczymy pochodne cząstkowe

4. Pochodne cząstkowe przyrównujemy do 0, szukamy minimum

Przykład złego uwarunkowania układu równań normalnych

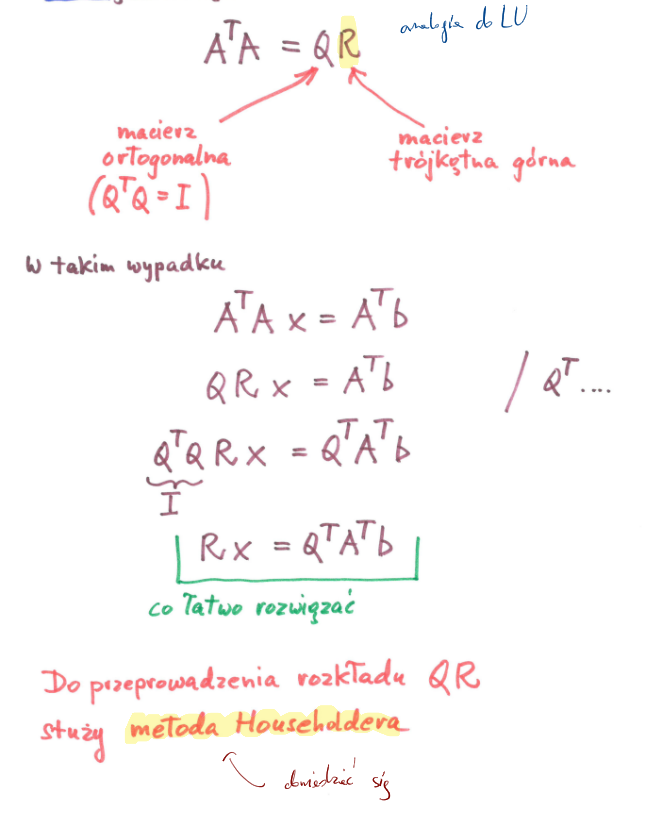
Układ równan normalnych należy rozwiązywać pomocą specjalnych metod, gdyż bywa źle uwarunkowany

mnożenie AA^T jest niebezpieczne

Mnożenie macierzy w arytmetyce zmiennoprzecinkowej może zmienić rząd macierzy i spowodować, że stanie się osobliwa.

Rozwiązanie problemu złego uwarunkowania - rozkład QR

Ogólny wzór dla metod iteracyjnych rozwiązujących układy lin. rów. alge.

Ax = b

Tworzymy ciąg kolejnych przybliżeń rozwiązania x:
x⁽⁰⁾, x⁽¹⁾
które obliczamy za pomocą wzoru

x⁽ⁿ⁾=M⁽ⁿ⁾x^(n-1)+c⁽ⁿ⁾

Główna trudność - jak skonstruować M, c, aby uzyskać szybką zbieżność

Metody stacjonarne i niestacjonarne

Metoda stacjonarna - M⁽ⁿ⁾ i c⁽ⁿ⁾ nie zależą od n

Metody niestacjonarne - M⁽ⁿ⁾ i c⁽ⁿ⁾ zależą od n

Metoda Richardsona

Analogiczna do metody Picarda

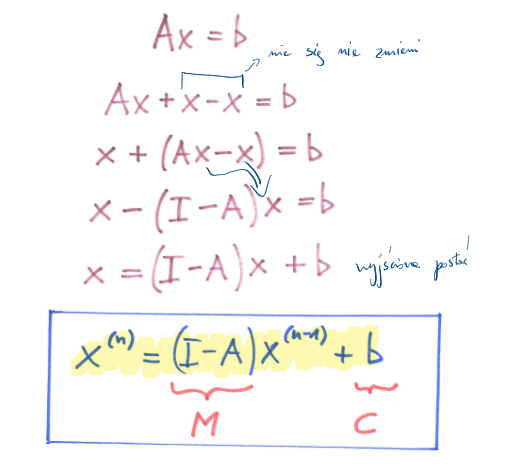
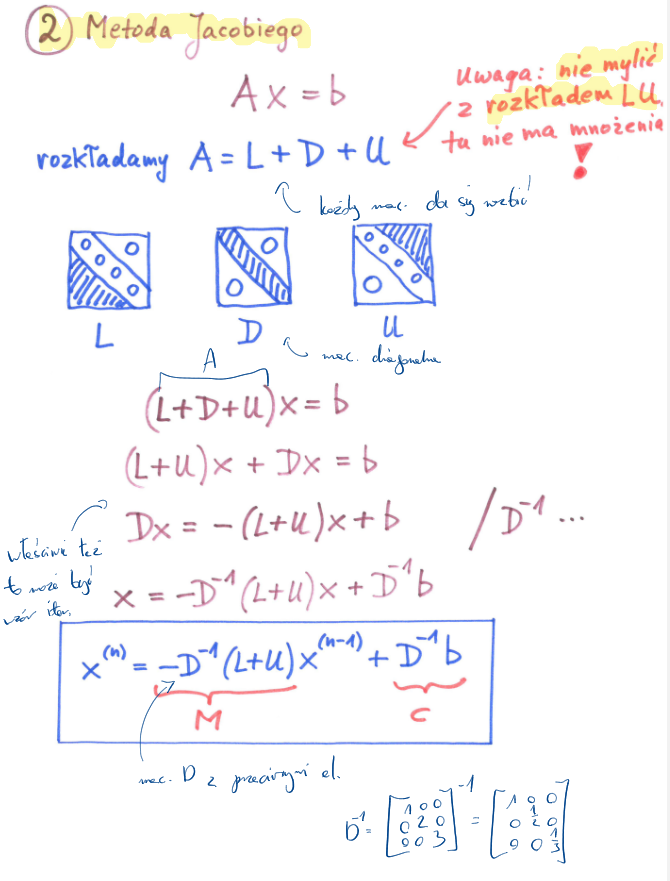
Metoda Jacobiego

A = L + D + U

D^-1 - łatwo obliczyć

Metoda Gaussa - Seidela

Wzór operacyjny - do obliczeń kolejnych przybliżeń
Wzór teoretyczny - do sprawdzenia zbieżności

Metoda sukcesywnej nadrelaksacji (SOR)

Sucessive over-relaxation

Younga i Frankela

Parametr ω - dobierany tak aby uzyskać szybką zbieżność

Zbieżność stacjonarnych metod iteracyjnych

Z tw. Banacha o kontrakcji, aby iteracje były zbieżne, odwzorowanie Φ(x) musi być zwężające

W naszym przypadku Φ(x) = Mx +C

Warunek dostateczny zbieżności:

||M|| < 1

Warunek konieczny i wystarczający:
ρ(M) < 1 - promień spektralny M

Można też pokazać, że w metodach [Jacobiego, Gaussa - Seidela i SOR] warunek || MI_∞ < 1 będzie spełniony jeżeli A jest diagonalnie silnie dominująca,

przy czym w SOR musi być też spełniony warunek 0<ω<2

Iteracyjne poprawianie rozwiązań w metodach bezpośrednich

Metody bezpośrednie dają x(0) z błędem maszynowym e(0)

Możemy skorygować błąd stosując poprawki w podwyższonej precyzji.