Geometry Honors: 9.5 Perform Rotations to 9.7 Identify and Perform Dilations

Rotation

a transformation in which a figure is turned about a fixed point, called the center of rotation

CW (rotation notation)

clockwise

CCW (rotation notation)

counter-clockwise

90° CCW about the origin

(x,y) → (-y,x)

180° CCW or CW about the origin

(x,y) → (-x,-y)

270° CCW about the origin

(x,y) → (y,-x)

What is 90° CCW about the origin the same as?

270° CW about the origin

What is 270° CCW about the origin the same as?

90° CW about the origin

When rotating a line, what is the same?

CW and CCW

What happens when a line is rotated 90° or 270°?

The resulting line is perpendicular to the original line.

What happens when a line is rotated 180°?

The line rotates back onto itself (no change, same equation).

Performing rotations about a non-origin center

1. Graph pre-image and plot center of rotation
2. Write vectors formed from the center of rotation to each vertex (in component form)
3. use rotation rules about the origin to rotate the vectors
4. apply the rotated vectors from the center of rotation to graph new points

Composition of transformations

when two or more transformations are combined to form a single transformation

Glide reflection

when there is a translation then a reflection

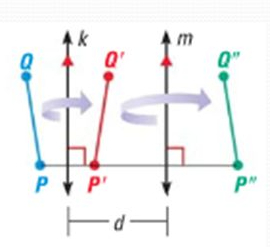
Reflection in Parallel Lines Theorem

If lines k and m are parallel then a reflection in line k followed by a reflection in line m is the same as a translation

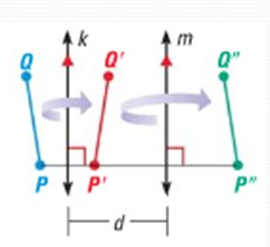
Properties of Reflection in Parallel Lines Theorem

1. if p" is the image of p, then line pp" is perpendicular to both k and m

2. pp" = 2d where d = distance between k and m

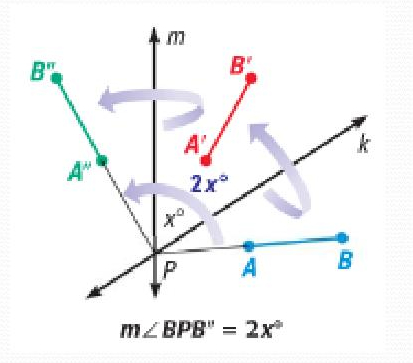
Reflections in Intersecting Lines Theorem

If k and m intersect at point p then a reflection in line k followed by a reflection in line m is the same as a rotation about point p

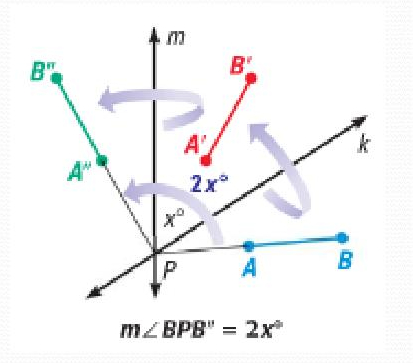
Properties of Reflections in Intersecting Lines Theorem

the angle of rotation is (2x)° where x is the measure of the acute (or right) angle formed by k and m

Dilations

an enlargement or reduction of a figure with respect to a fixed point, called the center of dilation

Unlike translations, reflections, and rotations, what do dilations produce?

similar figures

Scale factor

k, that tells how much a figure is enlarged (k>1) or reduced (0<k<1)

Rule for dilation about the origin

P(x,y) → P'(kx,ky)

Performing dilations about a non-origin center

1. Graph pre-image and center of dilation
2. Write vectors from center of dilation to each vertex
3. Apply scale factor to each vector, ⟨a,b⟩ → ⟨ka,kb⟩
4. Use dilated vectors to plot the image, give coordinates of image

How to identify the center of dilation

draw lines through each pair of corresponding vertices, the center of dilation is the point of intersection

How to identify the scale factor

compare corresponding lengths OR compare corresponding vectors