8) Groundwater flow equations

explain this

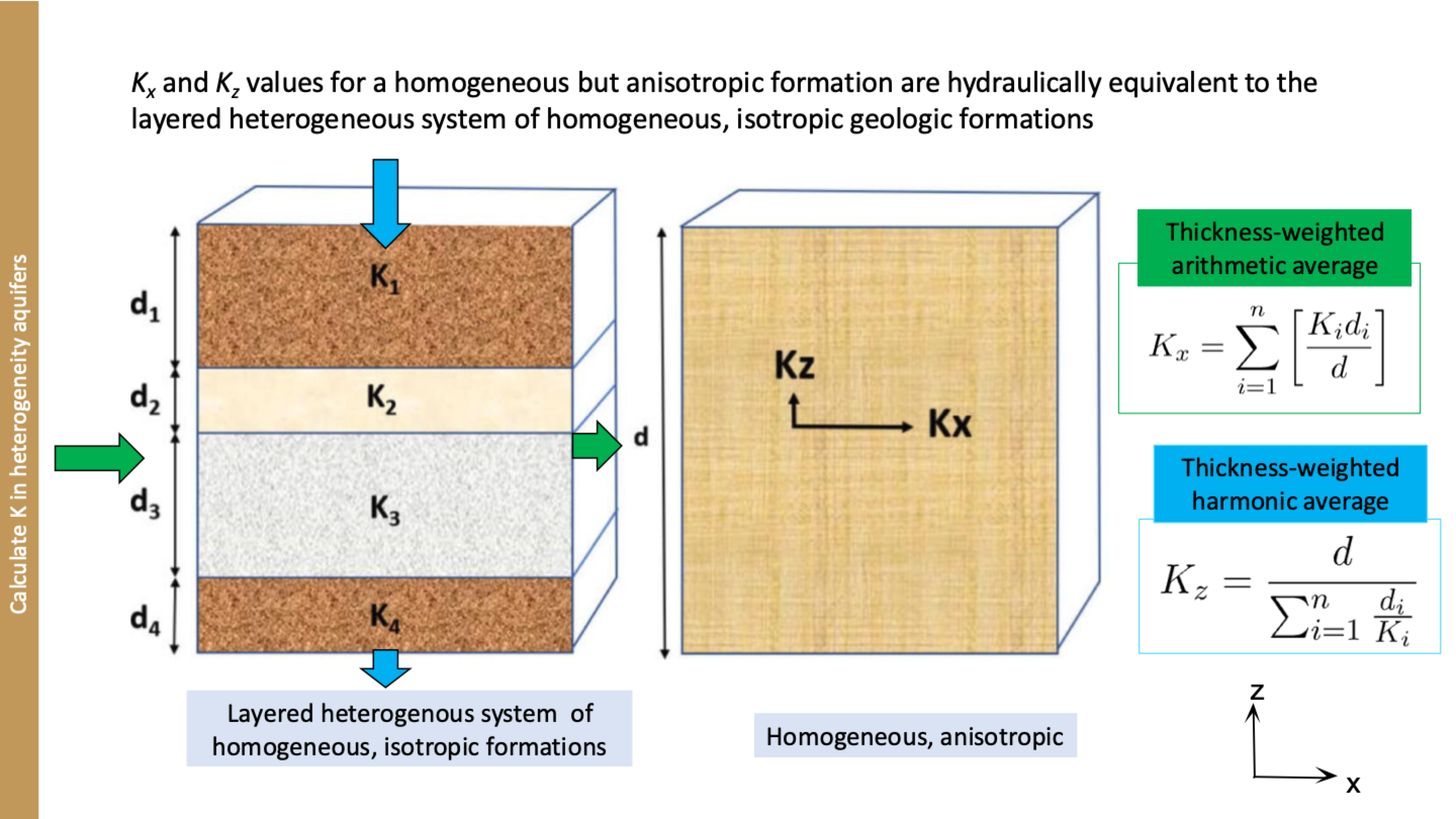
layered system, 3 thicknesses with 3 K values
difference in hydraulic head across the units is the same and the same distance travelled

total Q = Q1+Q2+Q3 = K
Q = -KA∆h/∆L = area in this case its thickness

total Q = -K1b1∆h/∆L + -K2b2∆h/∆L + -K3b3∆h/∆L
hydraulic gradient out because it’s the same for each part

Q = -∆h/∆L * sum of Kibi

steady state vs transient conditions

steady state: mass of water in REV is constant, inflow=outflow
heads, gradients, flow rates do not vary with time

transient conditions: mass of water in REV varies with time, inflow does not equal outflow, heads, gradients, flow rates vary with time

which are these examples

first: anisotropic, heterogeneous
spatial gradient, K is allowed to vary in space

second: anisotropic, homogeneous
k does not vary in space (outside of derivative), but diff K for each direction

third: isotropic, homogeneous
K is not in equation

forth: steady state

darcy’s law describes what?

mass fluxes

how do we get change in mass flux across REV with 1D flow

rate of change of density and specific discharge as you move across x distance

increasing in slope means head is falling, water coming out of storage

increase in flow = more water = less head

specific yield in a groundwater equation means?

unconfined aquifer

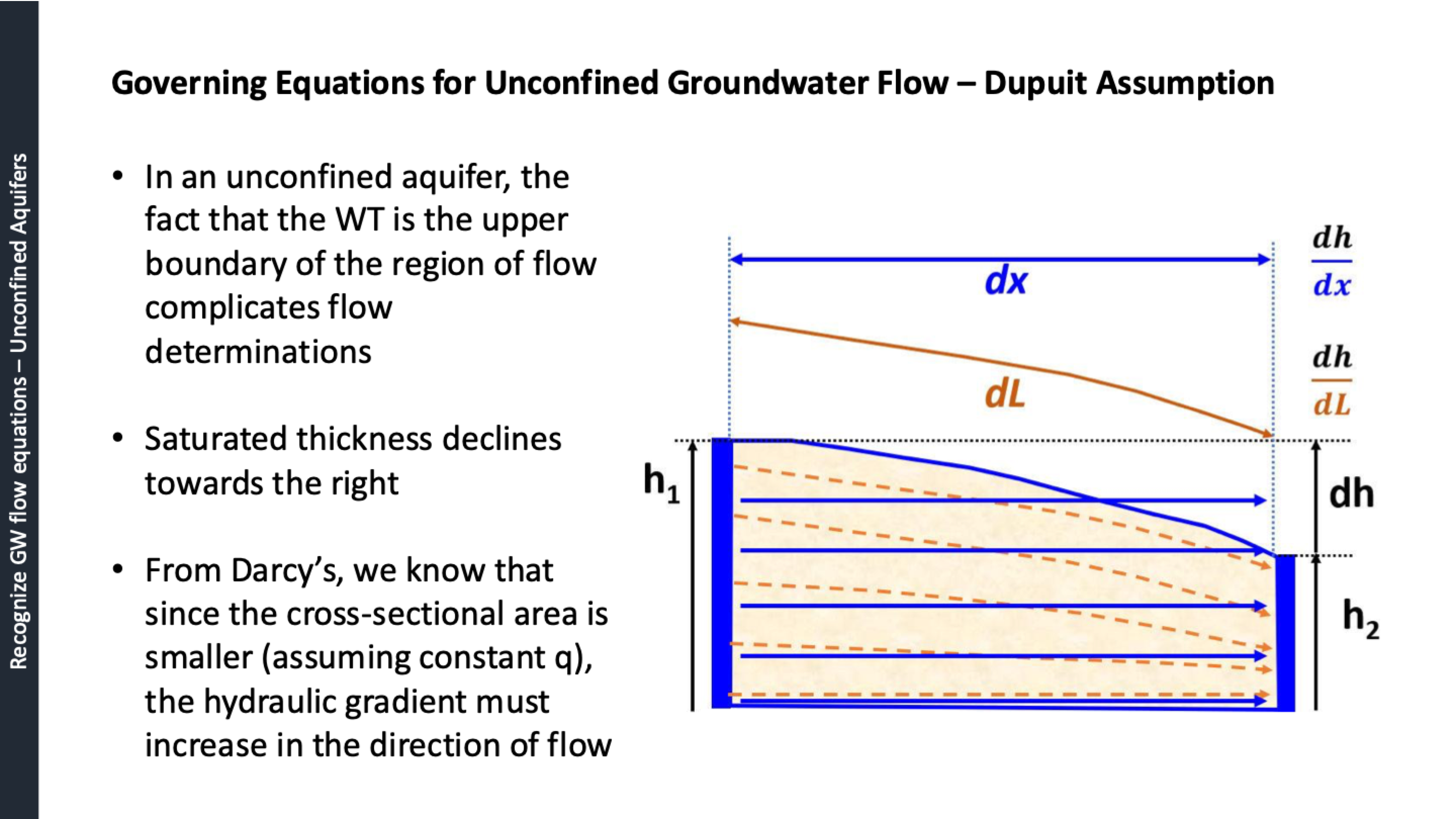
explain this, what assumption is it?

cross-sectional area is smaller to the right, so hydraulic gradient must increase considering constant flow

dupuit assumption: change in head probably won’t be significant, so ignore that it curves and just get area instead of doing dL, get dx
assume steady state

what is the procedure to solving a problem

identify boundaries

choose appropriate form of flow equation

specify initial conditions (steady state flow equations have no time in them, so we don’t need to specify initial conditions)

specify boundary conditions (Specified head boundary, or specified flux boundary)

specify material properties

solve the equation

details on specified head boundary

dirichlet

head is known at the boundary of the flow region

boundary forms an equipotential, adjacent equipotentials must be parallel to this boundary

model calculates flow rates at the location where head is specified

details on specified flux boundary

neumann

no flow or constant flow
no flow: perpendicular to equipotentials
constant flow: recharge or leakage applied to boundary

model calculates the head at the location where the flux is specified

how will the boundary look with recharge vs no recharge at the water table (WT)

no recharge, WT is a flow line, perfectly perpendicular

recharge: WT is not a flow line, equips are at an angle to WT

details on no flow boundary configurations

divide between the regions

no flow on the edge too, not the exit of the orange flow, the fact that it’s the boundary means its no flow

there is recharge and no flow so it’s specified flux boundary

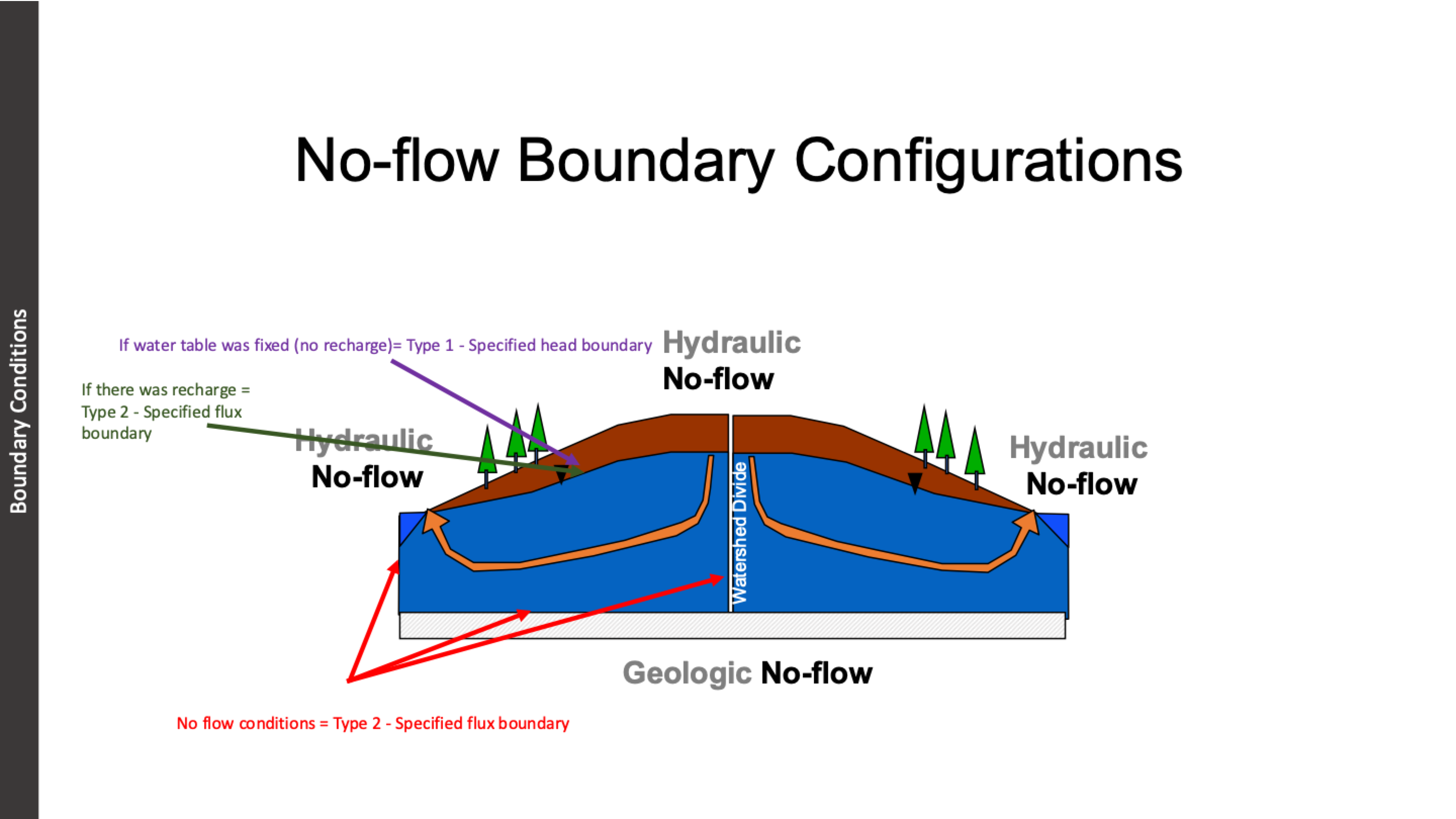
if there is no recharge and we know the height of the water table, what kind of boundary is that? why?

specific head

we know head at water table

examples of physical boundaries

no flow boundary at low K rock

constant head boundary at lake

water table with recharge AND without recharge

faults (can restrict or enhance K)

any major disruption in hydrogeologic unit disrupts boundaries as well

seawater-freshwater interface (limits flow, forces fresh unconfined GW to discharge along the coast)

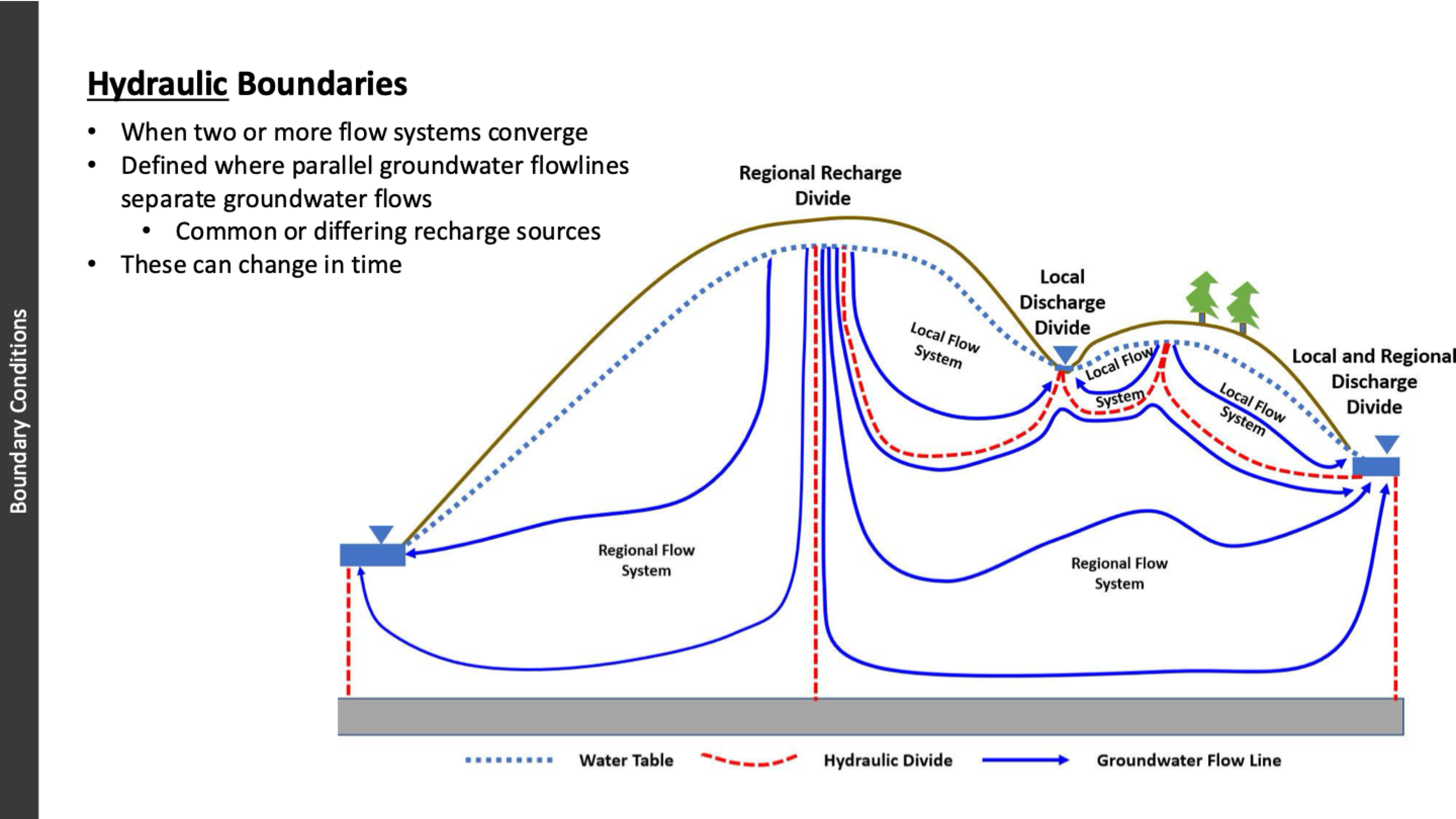
examples of hydraulic boundaries

when two or more flow systems converge

parallel groundwater flowlines separate groundwater flows
common or differing recharge sources

what are methods of solution for GW flow equations

analytical: give exact solutions to the eqtns
restricted to simple systems with regular geometry (homogeneous, isotropic, 1D, 2D)

graphical: flow nets for steady state, 2D problems

numerical: computers give approximate solutions to more complex problems by breaking the domain into small regions