Searching

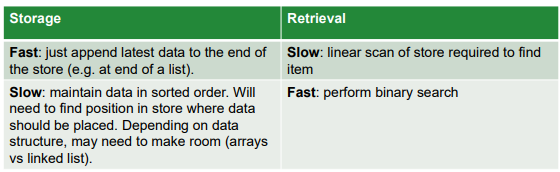
Data Storage and Retrieval

Fundamental operations:

• Put data item in store

• Retrieve specific item

If storage is quick, retrieval will likely be slow

If storage is careful, retrieval will be fast

Theoretical Time Complexity

The relationship between size of the input and algorithm running time

• Let N be the size of the input

• Characterize runtime of the algorithm as a function of N

Big-O Classes

captures the upper bound on time required for the input

Denoting the size of the input by N, algorithms are classified into classes:

• O(1) – constant time (time not affected by N) 

• O(log N) – logarithmic time (better than linear) 

• O(N) – linear time (time proportional to N) 

• O(N log N) – (worse than linear) 

• O(N² ) – quadratic time (time proportional to N² ) 

• O(N³ ) – cubic time (time proportional to N³ ) 

• O(2^N) – exponential time (very very slow …)

Linear Searching - Process

For an unsorted linear array A containing N integers

• find index of first occurrence of integer x

• If x is not present in array, return -1

Need to scan through array elements, checking for X and for the end of the array

ls(a[], x) {
	for (i = 0 to a.length)
	{
		if (a[i] = x)
		{
			return i;
		}
	}
	return -1
}

Linear Search Algorithm

• Let N be the size of the input array 

• Then, the foregoing linear search algorithm has complexity O(N)

• Linear complexity

• Runtime grows in direct proportion to input

Does Binary or Linear Search have better Theoretical Time Complexity?

binary search

linear stays at O(N) even when the list is sorted

Binary Search

To find X in array A, which has N sorted elements:

Look at element A[M], where M is the midpoint of A; 

• if X=A[M] X found

• if size(A)=1 && X!=A[M] X not in A

• if X<A[M] X in left half (LH) of A; Repeat 1 for LH

• if XA[M] X in right half (RH) of A; Repeat 1 for RH

What Type of Array can Binary Search be used on?`

sorted

Binary Search Algorithm

//search for X in sorted array A
int lo = 0;
int hi = N - 1;
int mid; //next element to try
while (lo <= hi) //while subarray size >= 1
{
	mid = (lo + hi)/2;
	if (A[mid] == X)
	{
		return mid;
	}
	if (X < A[mid])
	{
		hi = mid -1; //go left
	}
	else
	{
		lo = mid + 1; //go right
	}
}
return -1; //not found

Binary Searching: O(log₂N)

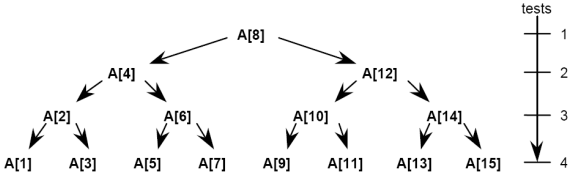
• N=1,2,4,8,16,32,64,128,… at most 1,2,3,5,6,7,8,… comparisons, respectively; i.e., at most (log2N)+1 comparisons

• N=15 tree, at most 4 comparisons

• Here, A is indexed from 1

• Nodes: show array elements to be tested

• Arrows: show next element to test after non-mat

Comparing Search Efficiencies

Binary search is in complexity class O(log N)

Linear search is in complexity class O(N)