Cosmology-First Test

Astronomy

(Greek): astron= star, nomos= district or abode.

1. Study of the universe

Solar System

The sun and all bodies which orbit around it

Galaxy

Huge grouping of usually hundreds of billions of stars, as well as gas and dust.

Universe

Turning; everything natural created by God; everything that exists can be measured

Astrology

Getting information or meaning from the stars, predicting the future

Exponential Notation

1 × 10^9 = billion, etc. etc. 10^-6= 1 millionth

Lightyear

Distance, speed of light= 186,000 miles/second

3000,000 km/s= cosmic speed limit

Trivium

Foundational: grammar, rhetoric, and logic

Quadrivium

Geometry, arithmetic, music, and astronomy

Astronomy was the basis of ________ and _________

time, calendars (farming, migrating, and navigation)

Day

Sun compared to cardinal points on horizon (local meridian)

Year

Sun compared to where the stars in the sky are.

Month

Moon-moonth

Constellations

Originally est. as navigational “sky marks” not affected by earthly influences.

Don’t have to look like what they’re supposed to rep, 88 official

Celestial Sphere

Motions appear spherical at cursory glance, so pick a special coordinate system.

Declination

Analogous to latitude

Right ascension

Analogous to longitude

Sexagesimal System

Angular measure_ by sixties.

Sun and moon are 30 arc minutes in diameter

North and South Celestial Poles

At ends of rotation axis.

If a star is near this point, it makes an excellent navigational device since the pole doesn’t move and is always visible except from the equator

Celestial equator

½ between poles, perpendicular to axis

Ecliptic

The path of the Sun among the fixed stars.

Zodiac

The 12 constellations the Sun passes through is (zone of the animals)

Vernal and Autumnal Equinoxes

Where the ecliptic crosses the celestial equator.

First day of fall and first day of spring, exactly 12 hours of day and night everywhere on Earth (except for the poles)

Solstices

hen the sun is furthest above and below the celestial equator; 23.5 degrees

Nadir

Point directly beneath your feet

Celestial Meridian

Great circle which passers through the N point, Zenith, South point, and Nadir

Sidereal Day

Celestial sphere spun every 23 hr, 56 min, and 4 secs!

Solar Day

Sun returned to the same place (altitude and an azimuth in the sky every 24 hrs) Rises 4 mins later every day.

Cause of Seasons

23.5 tilt of the Earth’s equator with respect to the ecliptic (the plane of the Earth’s orbit), or the tilt of the Earth’s rotational axis with respect to a perpendicular to the ecliptic.

Insolation

Curvature of the Earth spreads the collimated bundle of sunlight over unequal areas depending on the elevation of the sun (in coming solar radiation)

Solstice principle

Different rising and setting positions of the sun through the year was used by the ancient people for establishing accurate calendars.

North Pole

Emphasize ecliptic and 6-month long day and night

Arctic Circle

Summer Solstice

Tropic of Cancer

Sun at Zenith and at noon, the shadows disappear

Local hour angle (LHA)

The angle measured westward along the celestial equator from the local meridian to the hour circle (meridian) of the object.

Day

Time between successive transits (local meridian crossings) of a celestial object. From the meridian back to the meridian.

Local Sidereal Time (LST)

Local hour angle of the vernal (local star time)

Local Apparent Solar Time (LAST)

Local hour angle of the sun plus 12 hours (to make the day change at midnight, i.e. when Sun is at “lowest” point); the time that sundials keep (not watch)

Ante Meridian (AM)

Before the local meridian

Post meridian (PM)

After or past the local meridian

Sun’s eastward motion varies through the year due to…

• Sun moves along the ecliptic, NOT the equator

• Earth’s orbit is an eclipse, which makes the sun appear to move fastest when we are closest to it and slowest when furthest from it.

Mean sun

An imaginary sun which travels uniformly along the celestial equator, and whose motion matches the average motion of the real sun.

Local mean solar time (LMST)

Local hour angle of the mean (fictitious) sun plus 12 hours

Analemma

Depicts both the deviation of the true sun from uniform motion as well as the seasonal varying altitude of the real sun through the year.

The international date line

When you cross it going to the west you lose a day. Crossing from west to east you dain a day. Where it’s placed is arbitrary.

Daylight savings time

Purpose is to shift daylight hours into the evening i.e., sunrise occurs very early in the spring and summer months in the mid latitudes.

Julian Calendar

Every fourth year would have an extra day, a leap year added to the last month of the year which was Feb, only had 29 days in it at the time. (46 BC)

Gregorian Calendar

All years evenly divisible by 4 are leap years, except century years (1600, 1700, 1800, etc.) if they were divisible by 400

(2000 was not, 2100 will)

Sidereal Period

27.3 days is time for moon to complete its 360 degree orbit.

Synodic Period

Difference due to Earth’s orbital motion around the sun.

29.5306 days, Moon must go on extra 2 days and to make up for the ~27 degrees that the Earth moved in its orbit

Moon Phase

Moon illuminated by the sun and because of this and the fact that it’s a sphere

Blue Moon

2 full moons in the same month, once every 2-3 years.

New Moon

Will be wherever the sun is

Does the moon rotate?

Yes. Spin orbit synchronization.

Geometry of a solar eclipse

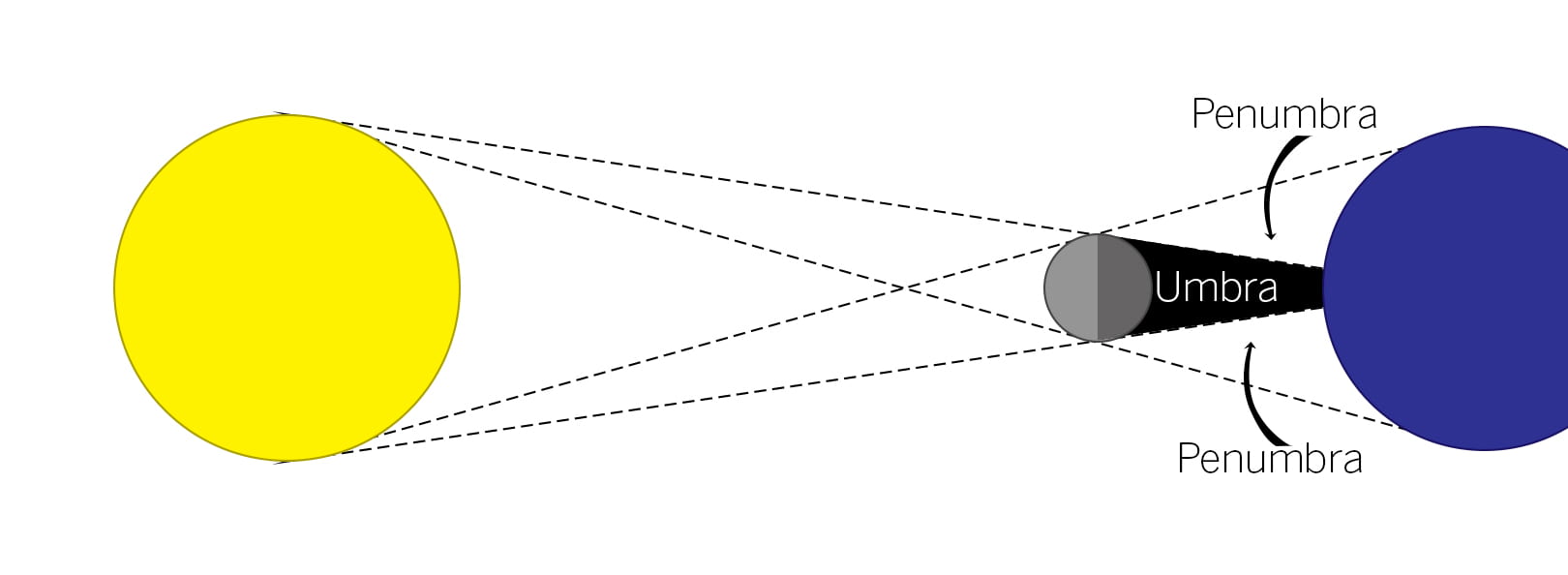
Conditions of a lunar eclipse

Full moon, moon at or near a node (on or near the ecliptic)

Why don’t lunar eclipses happen every month?

• 5 degree inclination of the moon’s orbit with respect to the ecliptic and usually isn’t on the ecliptic at full (or new moon)

• If it was the same places, we'd have them every six months an in the same month.

  • But we have the regression of nodes, a rotation of the line of apses so that eclipse season progress to a different times of the year.

Regressions of nodes

A rotation of the line of apses, so that eclipse seasons progress to different times of the year (18.6 years)

Conditions of a solar eclipse

New moon, moon at or near a node

Aristotle’s Arguments for a spherical Earth

1. Earth was a sphere because its shadow on the moon during a lunar eclipse is obviously curved.

2. Observes who travel in latitude (N+S) on the Earth see different stars change their altitude.

3. As ships approach port they are seen gradually from the mast down, not in their entirety, so this must be because of Earth’s curved horizon

AU

Known accurately from measuring distances to inner planets via radar ranging.

Pythagoras

Concentric crystalline spheres, one for the stars and each moving celestial body (sun, moon, planets)

Sphericity of ALL celestial objects since that’s the perfect shape. Curved shape of moon’s terminator.

Aristotle

Correctly understood the Moon’’s phases as well as lunar and solar eclipses

Argued for a spherical Earth.

Parsec

Distance to a star which exhibits a parallax of 1 _____ due to the Earth’s baseline of 1 AM.

1 _________=3.26 light years = 19 trillion miles.

Parallax Equation

d=1/pie (but not pie) or r=1/pie (but not pie).

Pie= 0.1 —> d=1/0.1=10 pc

Pie= 0/01 —> d=1/0.01=100 pc

Parallax

The apparent shifting of an object with respect to more distant objects because of the changing of the observer’s perspective. (position)

ex. the finger in front of the blinking eyes trick. r=1/pie

1838

Parallax first detected in _____

Parallax angle

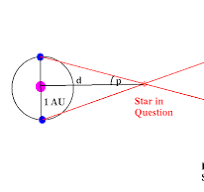
Stellar parallax

Stellar distances to the nearthest star.

Moving platform is the orbiting Earth around the sun, the baseline being the distance from the Earth to the Sun defined as the astronomical unit (AU). As the Earth orbits the sun, stars will appear to shift their positions which can then be employed to determine their distances from the Earth.

Visible effects of precession

NCP travels in a circle with a 26,000 year period, thus shifting the pole star through the ages.

That the vernal equinox passes eastward through through the zodiac, passing through a new constellation every 2000 years.

Precession

Caused by the gravitational tugging of the sun and in lesser part the Moon to attempt to right the Earth’s equator and pull it into alignment with the ecliptic

Since the Earth has angular momentum, it wants to keep its axis always pointed in the same direction, and so pulling creates a torque that results

Saros Cycle

The identical eclipse —> every 18.6 years and a 1/3 of the way over.

Anomalistic month

distance from the earth, 27.55455

Nodical month

Respect to the node, 27.2 days

Synodic Month

Moon phase, 29.5306 days

To have an eclipse of the same hype the following conditions

Moon must be at the same phase again (new or full) (synodic month)

When at that phase, the Moon must be in the same place with respect to the node (medical month)

Sun and moon must have the same distances from the Earth again (anomalistic month)

(Superior Planets) Solve the triangle for the planet’s distance

PS= (1 AU) cos(angle PSQ)

(Inferior Planets) Measure the elongation angle with a sextant and we can solve for the trigonometry relation

x= (1 AU) sin(elongation angle)

Superior planets

Those further from the Sun than the Earth (Mars, Jupiter, and Saturn)

(Superior Planets), Opposition

Planet on opposite side of Earth away from Sun

(Superior Planets), Connection

Planet on opposite side of Sun away from Earth

(Superior Planets), Quadrature

Sun-Earth-Planet angle is 90 degrees

Greatest Western Elongation

When an inferior planet is furthest west of the Sun as seen from Earth

Sun-planet-earth angle is 90 degrees

Greatest Eastern Elongation

When an inferior planet is furtherst east of the Sun as seen from Earth

Sun-planet-earth angle is 90 degrees

Superior Conjunction

When inferior planet lines up with Earth and Sun but is on the opposite side of the Sun from the Earth.

Tycho Brahe

Accurate and voluminous pre-telescopic observations from his royally-funded observatory

Found evidence that the Ptolemaic system was untenable (Guest star, new comet)

Couldn’t observe stellar parallax, meaning that the Earth couldn’t move

Cosmology: stationary Earth with the Sun orbiting it, but all other planets orbited the Sun

Inferior Conjunction

When inferior planet lines up in between the Earth and Sun

Inferior P

Those closer to the Sun than Earth (Mercury or Venus)

Nicholas Copernicus

Polish scholar, known for his mathematical and astronomical insight

Didn’t like ptolemaic geocentric system, it did away with Greek uniform circular motion

Heliocentric

Heliocentric Universe

Ptolemy’s model that became accepted as reality

Everything changes to nothing changes

Earth-decay, change, everything eventually grinds to a halt if you start moving.

Moon-boundary between earthly and heavenly, always moving, its face always changing (phases). But always same face (spin-orbit lock)

Mercury, Venus, Sun, Mars, Jupiter, Saturn in order of their speed (slowing down)

Stars, Primum Mobile, Heaven itself (unchanging)

Johannes Kepler

German astronomer, mathematician, and astrologer

Believed the heliocentric model, and needed accurate data to attempt to find mathematical formula which would describe it.

Fit Mars’ orbit to an ellipse, finally overcoming the prejudice for the circle being the “perfect” shape.

Ellipse Geometry

Major axis, semi major axis, minor axis, focus

eccentricity = distance from focus to center/semimajor axis

Eccentricity

ranges from zero (a circle) to 1 (a parabola)

Kepler’s 1st Law

All planets move around the Sun in ellipses with the Sun at one focus of the ellipse

Kepler’s 2nd Law

The straight line joining a planet to the Sun sweeps out equal areas in e

Kepler’s 3rd Law

The squares of the sidereal periods of the planets is directly proportional to the cubes of their semimajor axes.

Kepler’s 3rd Law equation

P² = ka³

p= sidereal period (years)

a= semimajor axis (AUs)

k= proportional constant to make the units come out correctly, (1)

Galileo Galilei

Italian scientist and mathematician, arguably the originator of experimental science; test a hypothesis by examining nature, don’t assume it’s correct because it seems logical in your mind.

Demonstrated that bodies of very different masses all fall at the same rate (acceleration is constant) , and idea totally against Aristotelian philosophy.

Galileo’s telescopic observations

Signaled the deathblow to the geocentric hypothesis

Discovered 4 satellites that orbited Jupiter in it’s equatorial plane

Proved that not everything orbited the Earth, and that Jupiter’s moons had no problem keeping up with Jupiter as it moved.

Moon revealed to be rough

Black spots moving indicating that the sun itself rotated

Venus showed that it exhibited phases similar to the moon. Had to orbit the sun