Tests for Sequences and Series
Multiple Choice
Call Kai1/39
Earn XP
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
40 Terms
Nth Term
an
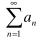
What does the nth term test for?
divergence
Nth Term diverges conditions
lim a ≠ 0
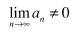
Geometric Series
arn
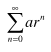
Geometric Series Convergence Conditions
l r l < 1
Geometric Series Divergence Conditions
l r l ≥ 1
What does the Geometric Series converge to?
the sum; S = a / (1-r)
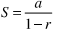
Telescoping Series
(an - an+1)
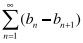
Telescoping Series Convergence Conditions
lim an = L; L has to be a finite number
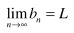
What does the telescoping Series converge to?
the sum; S = a1 - L
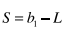
P-series test
1 / np
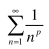
P-series test convergence conditions
p > 1
P-series test divergence conditions
0 < p ≤ 1
What if p = 1 in a p-series test?
divergent harmonic series
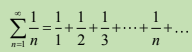
Alternating Series Test
(-1)n * an or (-1)n+1 * an+1
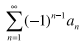
Alternating Series Test convergent conditions
0 < an+1 ≤ an (nonincreasing) & lim an = 0
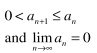
Alternating Series Test Remainder
l S - Sn l = l Rn l ≤ an+1
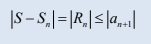
Integral Test conditions for f(x)
positive, continuous, and decreasing
Integral Test
an = f(n)
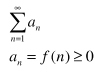
Integral Test Convergence Conditions
∫ f(x) dx converges, then series converges
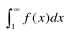
Integral Test Divergence Conditions
∫ f(x) dx diverges, then series diverges
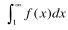
Ratio Test
an
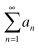
Ratio Test Convergence Conditions
lim l an+1 / an l < 1
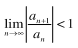
Ratio Test Divergence Conditions
lim l an+1 / an l > 1 or = ∞
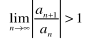
Ratio Test is inconclusive if?
lim l an+1 / an l = 1
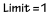
Root Test
an
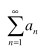
Root Test Convergence Conditions
lim n√l an l < 1
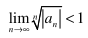
Root Test Divergence Conditions
lim n√l an l > 1
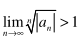
The root test is inconclusive when?
lim n√l an l = 1
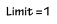
Direct Comparison Test
an
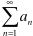
Direct Comparison Test Convergence Conditions
0 < an ≤ bn and bn converges
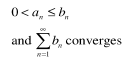
Direct Comparison Test Divergence Conditions
0 < bn ≤ an and bn diverges
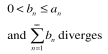
Limit Comparison Test
an
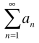
Limit Comparison Test Convergence Conditions
lim (an / bn) = L > 0 & bn converges
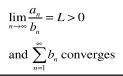
Limit Comparison Test Divergence Conditions
lim (an / bn) = L > 0 & bn diverges
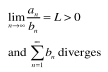
L must be what in limit comparison test?
finite and positive
Absolute vs. Conditional Convergence
once identified as convergence, use tests to see if l an l is convergent; yes- absolute or no- conditional
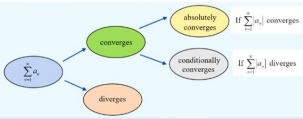
Sequence
a list; ex: 2, 4, 6, 8
Series
ex: 2 + 4 + 6 + 8
Recursive Definition (Implicit Definition) vs. Explicit Definition for Sequences
recursive- an+1 = an + x; explicit- an = 3n - 2
